3 Ways to Calculate the Volume of a Cube

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-15 08:07

A cube is a three-dimensional shape that has the same length, width and height. A cube has six square sides, all of which are the same length and meet at right angles. Finding the volume of a cube is very easy, all you need is to calculate length × width × height Cube. Since all edges of a cube are the same length, another way to calculate the volume is s ³, where s is the length of the side of the cube. Read Step 1 below to understand a detailed description of this process.

Step

Method 1 of 3: Raising the Cube's Three Edges

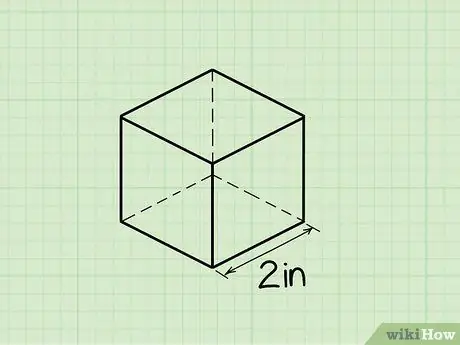
Step 1. Find the length of the side of the cube

Usually, if the problem asks for the volume of a cube, you will be given the length of the side. If so, you have everything you need to find the volume of the cube. If you're not doing the problem, but instead counting the original cube, measure the edges with a ruler or tape measure.

To understand the process of finding the volume of a cube better, let's follow an example problem as we go through the steps in this section. Say the cube has sides 2 cm long. This information will be used to find the volume of the cube in the next step

Step 2. Square the cube's side lengths

When you know the length of the side of the cube, raise it to the power of three. In other words, multiply by the number itself twice. If s is the length of the edge, multiply s × s × s (or simplified, s ³). The result is the volume of your cube!

• In essence, this process is the same as finding the area of the base and multiplying it by the height (in other words, length × width × height) because the area of the base is obtained by multiplying the length and width. Since the cube is a shape that has the same length, width, and height, this process can be shortened by simply multiplying by three.

• Let's continue our example problem. Since the side of the cube is 2 cm, its volume can be calculated by multiplying 2 x 2 x 2 (or 2³) =

  Step 8..

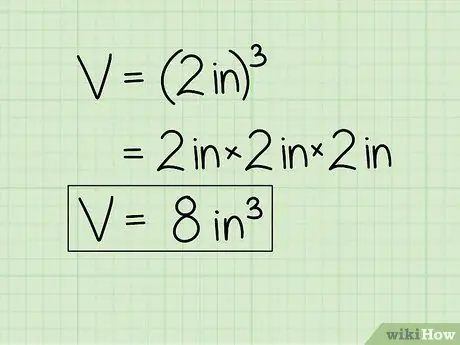
Step 3. Give the cubic unit of volume

Since volume is a measure of three-dimensional space, your answer must have cubic units. Usually, your answer will still be blamed if the unit is not cubic, even though the number is correct. So, don't forget to give the correct units.

• In the example problem, since the initial unit is centimeters (cm), the final answer must have the units "cubic centimeters" (or cm.).³). Thus, our answer is 8 cm³.
• If the length of the edge of the cube uses different units, the units of volume must be adjusted. For example, if the side of a cube is 2 “meters” instead of centimeters, the final unit of volume is cubic meter (m³).

Method 2 of 3: Finding Volume from Surface Area

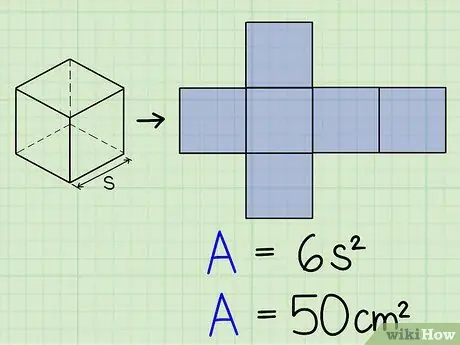
Step 1. Find the surface area of the cube

Even though the way easiest to find the volume of a cube is to use one of the edges, still there another way to find it. The side length of the cube or the area of the square on one of its faces can be derived from some other properties of the cube, which means that if you start with any of these pieces of information, the volume of the cube can be found by turning. For example, if you know the surface area of a cube, its volume can be found with divide the surface by 6, then root to find the length of the side of the cube.

From here, the volume can be searched in the usual way in Method 1. In this section, we will go through the process step by step.

• The surface area of a cube is found by the formula 6 s ², where s is the length of one of the edges of the cube. This formula is essentially the same as finding the surface area of a 2-dimensional shape of the six sides of a cube, then adding them all together. We will use this formula to find the volume of a cube from its surface area.
• For example, say that we have a cube whose surface area is 50 cm², but the length of the ribs is unknown. In the next few steps, we will use this information to find the volume of the cube.

Step 2. Divide the surface area of the cube by 6

Since a cube has 6 equal sides, the area of one side can be obtained by the surface area of a cube with 6. The area of one side is equal to the product of the two edges of the cube (length × width, width × height, or height × length).

In this example, divide 50/6 = 8, 33 cm². Don't forget that two-dimensional shapes have units square (cm², m², etc).

Step 3. Root the calculation result

Since the surface area of one side of the cube is equal to s ² (s × s), taking this root will give you the length of the side of the cube. Once you know the side lengths, you can find the volume of the cube using the usual formula.

In the example problem, 8, 33 is more or less 2, 89 cm.

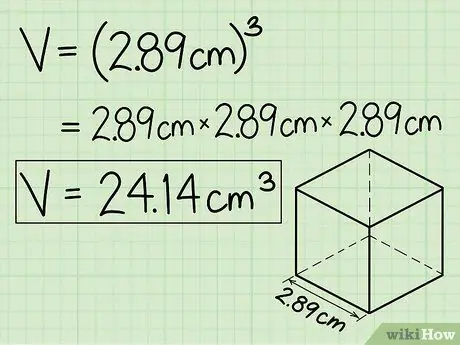
Step 4. Raise the edge of the cube by three to get the volume of the cube

Now that you have the length of the cube's side, simply cube that value (multiply by the number itself twice) to find the volume of the cube according to the steps in Method 1. Congratulations, you've found the volume of the cube from its surface area.

In the example problem, 2, 89 × 2, 89 × 2, 89 = 24, 14 cm³. Don't forget to add cubic units to your answers.

Method 3 of 3: Finding the Volume of the Diagonal

Step 1. Divide the diagonal on one side of the cube by 2 to find the edge

The diagonal of a square is 2 × the length of the side. Thus, if the information provided is only the diagonal of one side of the cube, you can find the edge by dividing the diagonal by 2. From here, you can simply search for the volume with the steps in Method 1.

• For example, say that one of the sides of the cube has a diagonal of 7 cm. We will find the side length of the cube by calculating 7/√2 = 4.96 cm. Now that you know the side lengths, the volume can be calculated by calculating 4.96³ = 122, 36 cm³.
• It should be noted, in general, that d ² = 2 s ² that is, d is the length of the diagonal of one side of the cube, and s is the length of the side of the cube. This is in accordance with the Pythagorean Theory, which states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. Thus, since the diagonals of one side of the cube and its two sides are a right triangle, d ² = s ² + s ² = 2 s ².

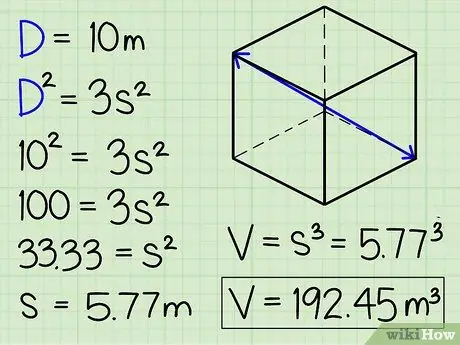
Step 2. Square the diagonal connecting the two opposite corners of the cube, then divide by 3 and the square root to get the length of the side

If the information provided is only the three-dimensional diagonal of the cube extending from one corner of the cube to the corner opposite, the volume of the cube can still be found. The three-dimensional diagonal of D becomes the hypotenuse of the right triangle formed with the cube's edges, and the diagonal of the square of the side of the cube "d". In other words, D ² = 3 s ², i.e. D = diagonal of a 3-dimensional shape connecting opposite corners of the cube.

• This is because of the Pythagorean Theory. D, d, and s form right angles with D as the hypotenuse, so we can say that D ² = d ² + s ². Therefore above we calculate d ² = 2 s ², it is certain that D ² = 2 s ² + s ² = 3 s ².

• For example, let's say that we know that the length of the diagonal connecting one of the corners at the base of the cube to the corner opposite its top is 10 m. To find the volume, enter 10 for each "D" in the equation:

  • D ² = 3 s ².
  • 10² = 3 s ².
  • 100 = 3 s ²
  • 33, 33 = s ²
  • 5, 77 m = s. From here, we just need to find the volume of the cube using the side lengths.
  • 5, 77³ = 192, 45 m³