- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Factors of a number are numbers that can be multiplied to get that number. Another way of looking at it is that every number is the product of multiple factors. Learning how to factor - that is, breaking down a number into its component factors - is a mathematical skill that is used not only in basic arithmetic but also in algebra, calculus, and others. See Step 1 below to start learning how to factor!
Step
Method 1 of 2: Factoring Basic Integers

Step 1. Write down your number
To start factoring, all you need are numbers - any number doesn't matter, but, in this case, let's use simple integers. An integer is a number that is neither a fraction nor a decimal (all positive and negative whole numbers are integers).
-
Suppose we choose the number
Step 12.. Write this number down on a piece of paper.
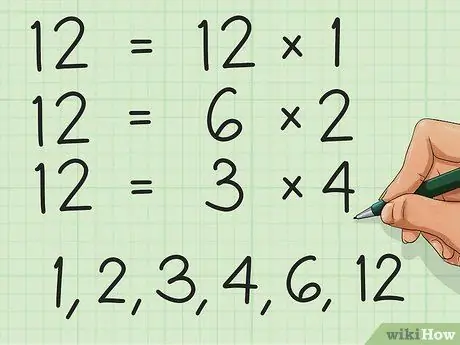
Step 2. Find the two numbers which when multiplied yields your first number
Any integer can be written as the product of two other integers. Even prime numbers can be written as the product of 1 multiplied by the number itself. Thinking of a number as a product of two factors requires backward thinking - you have to ask yourself, what multiplication produces this number?
- In our example, 12 has many factors - 12 × 1, 6 × 2, and 3 × 4 are equal to 12. Thus, we can say that the factors of 12 are 1, 2, 3, 4, 6, and 12. For this purpose, let's use factors 6 and 2.
- Even numbers are very easy to factor because every integer has a factor of 2. 4 = 2 × 2, 26 = 13 × 2, and so on.
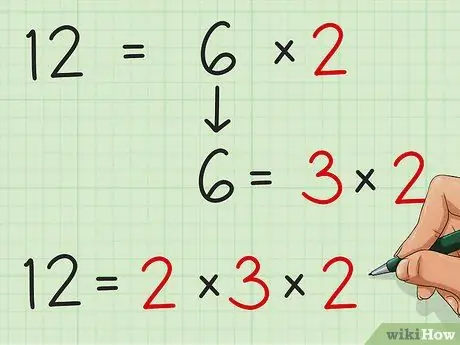
Step 3. Determine if your factor can still be factored
Many numbers - especially large numbers - can still be factored multiple times. When you find two factors of a number, if one has a factor, you can factor this number according to the factor. Depending on the situation, it may be advantageous or disadvantageous to do so.
For example, in our example, we have factored 12 into 2 × 6. Notice that 6 has its own factor - 3 × 2 = 6. So, we can say that 12 = 2 × (3 × 2).

Step 4. Stop factoring if you encounter a prime number
A prime number is a number that can only be divided by itself and 1. For example, 1, 2, 3, 5, 7, 11, 13, and 17 are prime numbers. If you factor a number and the result is a prime number, continuing to factor is pointless. There's no point in factoring it into itself times one, so just stop it.
In our example, we factored 12 into 2 × (2 × 3). 2, 2, and 3 are prime numbers. If we factor it again, we'll have to factor it into (2 × 1) × ((2 × 1)(3 × 1)), which is useless, so it's best avoided
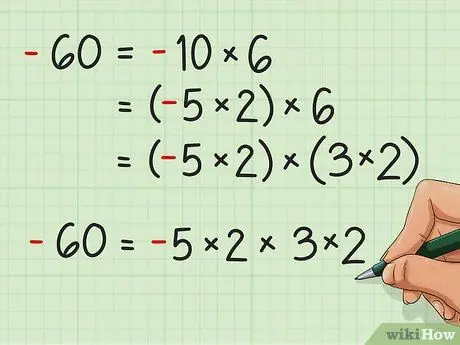
Step 5. Factor negative numbers in the same way
Negative numbers can be factored in the same way as positive numbers. The difference is that the factors must produce the number when multiplied, so if any of the factors the number must be negative.
-
For example, let's factor -60. See the following:
- -60 = -10 × 6
- -60 = (-5 × 2) × 6
- -60 = (-5 × 2) × (3 × 2)
- -60 = -5 × 2 × 3 × 2. Note that the product of one negative number and several odd numbers of negative numbers will have the same result. For example, -5 × 2 × -3 × -2 also equals 60.
Method 2 of 2: Strategy For Factoring Large Numbers
Step 1. Write your numbers above in a 2 column table
While it's usually easy to factor small integers, factoring large integers can be confusing. Most of us would find it frustrating to solve a number with 4 or 5 digits as prime factors using math. Fortunately, using tables makes this process much easier. Write your numbers above in a T-shaped table with 2 columns - you will use this table to record your factoring.
For this example, let's choose a 4 digit number to factor - 6.552.
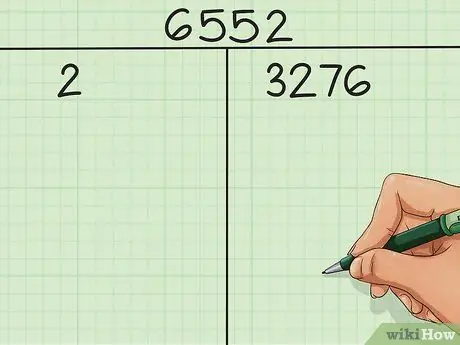
Step 2. Divide your number by the smallest possible prime factor
Divide your number by the smallest prime factor (other than 1) so that it has no remainder. Write the prime factors in the left column and write your division answer in the right column. As noted above, even numbers are very easy to factor because their smallest prime factor is always 2. However, odd numbers have different smallest prime factors.
-
In our example, since 6.552 is an even number, we know that the smallest prime factor is 2. 6.552 2 = 3.276. In the left column, we write
Step 2. and in the right column, write 3.276.

Step 3. Continue factoring numbers in this way
Next, factor the number in the right column by its smallest prime factor, not the number at the top of the table. Write the prime factor in the left column and the new number in the right column. Keep repeating this process - with each iteration, the number in the right column will decrease.
-
Continue our process. 3.276 2 = 1.638, so at the bottom of the left column, we will write the number
Step 2. again, and under the right column, we'll write 1.638. 1,638 2 = 819, so we will write
Step 2. and 819 under the previous column.
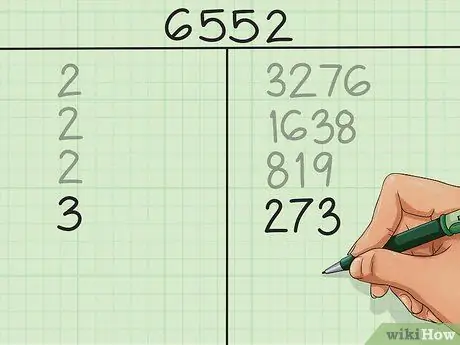
Step 4. Factor the odd numbers by trying small prime factors
It is more difficult to find the smallest prime factor of an odd number than an even number because the smallest prime factor is not 2. If you encounter an odd number, try dividing by a small prime number other than 2 - 3, 5, 7, 11, and so on - until you find the factor which can divide it without remainder. This is the smallest prime factor of the number.
-
In our example, we find 819. 819 is an odd number, so 2 is not a factor of 819. Instead of writing the number 2, we try the next prime number which is 3. 819 3 = 273 and there is no remainder, so we write
Step 3. and 273.
- When guessing factors, you should try all prime numbers up to the square root of the largest factor found. If you can't find a factor that divides a number without remainder, it's probably a prime number and you stop the factoring process.

Step 5. Continue until you find the number 1
Continue dividing the numbers in the right column using their smallest prime factor until you find the prime numbers in the right column. Divide this number by itself - so that the number in the right column remains and 1 in the right column.
-
Complete the factoring of our number. See the following for a detailed breakdown:
-
Divide by 3 again: 273 3 = 91, no remainder, so we write
Step 3. and 91.
-
Let's try the number 3 again: 3 is not a factor of 91, and the next prime (5) is not a factor either, but 91 7 = 13, without a remainder, so we write
Step 7. da
Step 13..
-
Let's try the number 7 again: 7 is not a factor of 13, and the next prime number (11) is not a factor either, but it is divisible by itself: 13 13 = 1. So, to complete our table, we write
Step 13. da
Step 1.. Factoring complete.
-
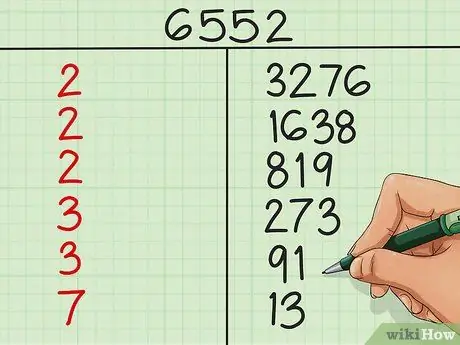
Step 6. Use the numbers in the left column as factors for your numbers
If you have found 1 in the right column, factoring is complete. The numbers in the left column are the factors. In other words, if you multiply all these numbers, you will get the number that is at the top of the table. If the same factor occurs multiple times, you can use the square sign to save space. For example, if there are 4 factors of 2, you can write 24 versus writing 2×2×2×2.
In our example, 6.552 = 23 × 32 × 7 × 13. This is a complete factorization of 6,552 into prime factors. The order of these numbers will have no effect; the multiplication result will still be 6,552.
Tips
- Another important thing is the concept of numbers prime: a number that has only two factors, 1 and itself. 3 is a prime number because its factors are only 1 and 3. However, 4 has a factor of 2. Numbers that are not prime are called composites. (However, the number 1 is neither prime nor composite - it is special).
- The lowest prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, and 23.
- Understand that a number is factor another number - so that the larger number can be divided by the smaller number without a remainder. For example, 6 is a factor of 24 because 24 6 = 4 and there is no remainder. However, 6 is not a factor of 25.
- Keep in mind that we are only talking about natural numbers - which are sometimes called counting numbers: 1, 2, 3, 4, 5… We will not be factoring negative numbers or fractions, as they are not appropriate for this article.
- Some numbers can be factored in a faster way, but this method works all the time, as a bonus, prime factors are sorted from smallest to largest when you're done.
- If the numbers are added and are multiples of three, then one of the factors of the number is three. (819 = 8+1+9 = 18, 1+8 =9. Three is a factor of 9 so it is a factor of 819.)






