- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
In geometry, an angle is the space between 2 rays (or line segments) with the same endpoint (aka vertex). The most common way to measure angles is to use degrees, and a full circle has an angle of 360 degrees. You can calculate the measure of one angle in a polygon if you know the shape of the polygon and the measures of the other angles, or in the case of a right triangle, if you know the lengths of the two sides. Additionally, you can measure angles using an arc or calculate them using a graphing calculator.
Step
Method 1 of 2: Calculating the Interior Angles of a Polygon
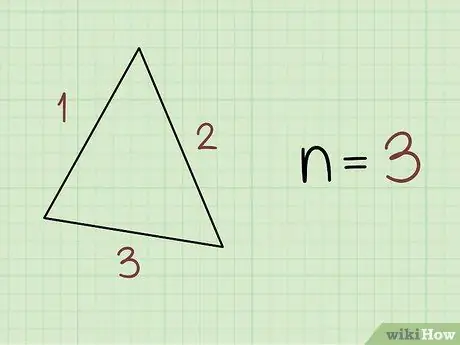
Step 1. Count the number of sides in the polygon
To be able to calculate the interior angles of a polygon, you first need to determine how many sides the polygon has. Know that the number of sides of a polygon is equal to the sum of its angles.
For example, a triangle has 3 sides and 3 interior angles, while a square has 4 sides and 4 interior angles
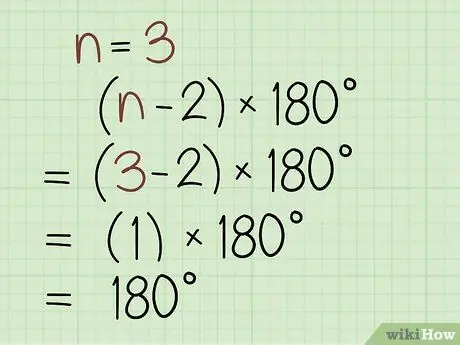
Step 2. Find the total size of all interior angles of the polygon
The formula for finding the total size of all the angles in a polygon is: (n - 2) x 180. In this case, n is the number of sides the polygon has. The total angle sizes in some common polygons are as follows:
- The total angles in a triangle (3 sided polygon) are 180 degrees.
- The total angles in a quadrilateral (4-sided polygon) is 360 degrees.
- The total angles in a pentagon (a 5-sided polygon) is 540 degrees.
- The total angles in a hexagon (a 6-sided polygon) are 720 degrees.
- The total angles in a triangle (a 7-sided polygon) are 1080 degrees.

Step 3. Divide the total angle size of all regular polygons by the sum of their angles
A regular polygon is a polygon whose all sides are the same length, so all the angles are the same. For example, the measure of each angle in an equilateral triangle is 180 3, or 60 degrees, and the measure of each angle in a square is 360 4, or 90 degrees.
Equilateral triangles and squares are examples of regular polygons, while the Pentagon in Washington, D. C., United States, is an example of regular pentagons, and stop signs are examples of regular octagons

Step 4. Subtract the total angle measure of the polygon by the sum of all the known angles to find the measure of the angles in the irregular polygon
If the polygons don't have the same side lengths and angle measures, you just need to add up all the known angles in the polygon. Then, subtract the total angle measure of the associated polygon from the sum of all the known angles to find the measure of the unknown angle.
For example, if you know that the 4 angles in a pentagon are 80, 100, 120, and 140 degrees respectively, add them up to get 440. Then, subtract that number from the total angle measure of a pentagon, which is 540 degrees: 540 - 440 = 100 degrees. So, the remaining angle is 100 degrees
Tip:
Some polygons have “shortcuts” to help you measure unknown angles. An isosceles triangle is a triangle with two equal sides and 2 equal angles. A parallelogram is a quadrilateral with the same lengths of opposite sides and the same measure of the diagonally opposite angles.
Method 2 of 2: Finding the Angles in a Right Triangle
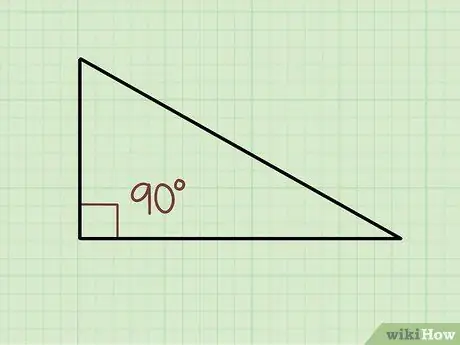
Step 1. Remember that in every right triangle there is only one angle that is equal to 90 degrees
By definition, a right angle always has a measure equal to 90 degrees, even if it is not labeled. So you will always know the measure of at least one angle and can use trigonometry to find the measure of the other two angles.
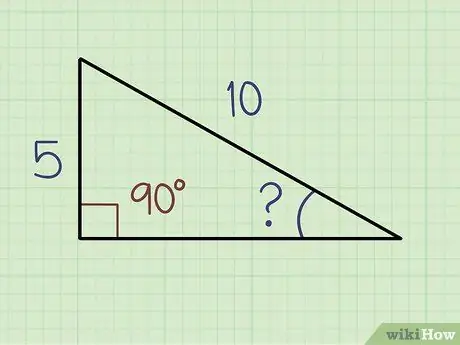
Step 2. Measure the length of the two sides of the triangle
The longest side of the triangle is called the "hypotenuse." The "side" side is the side next to the angle you want to find the magnitude of. The "front" side is the side opposite the angle you are looking for. Measure these two sides so you can determine the size of the remaining corners in the triangle.
Tip:
You can use a graphing calculator to solve equations or look up online tables that list the values of various sine, cosine, and tangent.
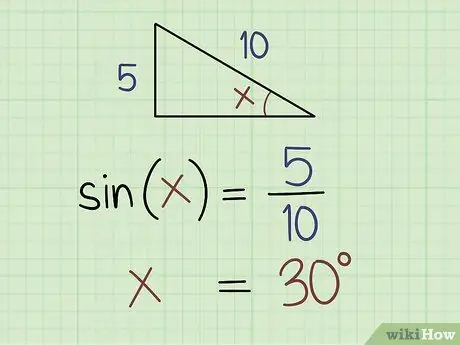
Step 3. Use the sine function if you know the length of the side and the hypotenuse
Plug the numbers into the equation: sine (x) = front hypotenuse. Say the length of the opposite side is 5 and the length of the hypotenuse is 10. Divide 5 by 10, which is equal to 0.5. Now you know that sine (x) = 0.5, which is equal to x = sine-1 (0, 5).
If you have a graphing calculator, just type in 0.5 and press sine-1. If you don't have a graphing calculator, use an online chart to find the value. You will find that x = 30 degrees
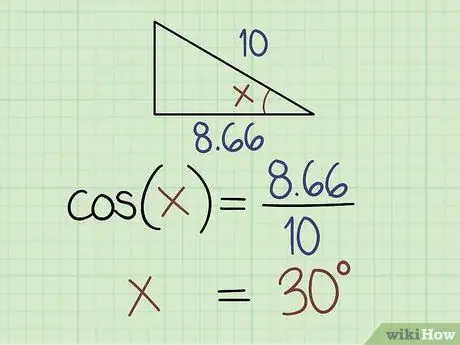
Step 4. Use the cosine function if you know the length of the side and the hypotenuse
For problems like this, use the equation: cosine (x) = side hypotenuse. If the length of the side is 1.666 and the length of the hypotenuse is 2.0, divide 1.666 by 2, which is equal to 0.833. So, cosine (x) = 0.833 or x = cosine-1 (0, 833).
Enter 0.833 into the graphing calculator and press the cosine key-1. Otherwise, look up the cosine value chart. The answer is 33.6 degrees.

Step 5. Use the tangent function if you know the length of the front and side
The equation for the tangent function is tangent (x) = front side. Say you know the length of the front side is 75 and the side length is 100. Divide 75 by 100, which is 0.75. That is, tangent (x) = 0.75, which is the same as x = tangent-1 (0, 75).
Look up the value in the tangent chart or press 0.75 on the graphing calculator, then tangent-1. Its value is equal to 36.9 degrees.
Tips
- Angles are named based on their size. As mentioned above, a right angle has a measure of 90 degrees. An angle that is less than 90 but more than 0 degrees is called an acute angle. An angle whose measure is more than 90 degrees and less than 180 degrees is called an obtuse angle. Angles with a measure of 180 degrees are called straight angles, while angles greater than 180 degrees are called reflex angles.
- Two angles that add up to 90 degrees are called complementary angles (the two angles other than a right angle in a right triangle are complementary angles). Two angles that add up to 180 degrees are called supplementary angles.






