Although precision and accuracy are often used interchangeably, they are actually very different words in math and science. Precision means that a measurement has nearly the same value each time it is made. For example, if you step on the scale 5 times in a row, a scale that has good precision will show the same mass each time. In math and science, calculating precision is very important to determine if your tools and measurements are working properly to get good data. Fortunately, calculating precision is quite easy.
Step
Step 1. Know the difference between precision and accuracy
Precision measures how well your tools work, not what they measure. Accuracy checks how accurate your answer is. For example, if your mass is 9 kg and your scale shows 8.7 kg, your scale is not accurate. If your scale shows 8.7 kg each time you weigh your mass, it is still precise, although not accurate.
Think of the two words in these archery terms: Accuracy is if we hit the center circle of the archery target (bullseye) every time we shoot. Precision is if we hit the same spot every time we shoot, even if that place isn't the target we want to hit.
Step 2. Record several measurements
To calculate precision, you need data about something. For example, if you want to check the precision of your scale, you can stand on it and record the number shown on the scale 15 times.
You must record multiple measurements of the same object under the same conditions in order to calculate precision. You can't weigh 10 different people and compare the results
Step 3. Find the mean or average of your data
To notice the change in precision, you have to compare your data to something. The mean or average is the center point of your data and is a good benchmark. To find the mean, add up all the measurements you took and divide the number by the number of measurements you took. If, when weighing your mass, you recorded the masses: 12 kg, 11 kg, 14 kg, 13 kg and 12 kg, your mean would be:
(12 kg + 11 kg + 14 kg + 13 kg + 12 kg) / 5 = 62 / 5 = 12.4 kg
. In other words, the average mass recorded is 12.4 kg.
You can also use numbers that you already know and don't need to use the mean. For example, you could use a 10 kg bag of potatoes and compare your figures to this number
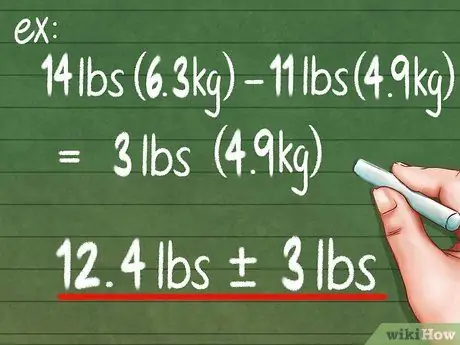
Step 4. Use standard ranges for simple precision calculations
Range is the easiest way to determine precision. To calculate it, just take your highest score and subtract your lowest score from that highest score. For the example above, 14 kg – 11 kg = 3 kg. So you can report that the object you are measuring is 12.4 kg ± 3 kg.
- The value of ±3 kg is your precision measurement. This means that this scale is only precise in the range of 6 kg or 3 kg heavier and 3 kg lighter.
- The ± symbol can be read as “more or less”.
- This method is the most frequently used method for calculating precision. Although simple, ironically this method is not very precise.
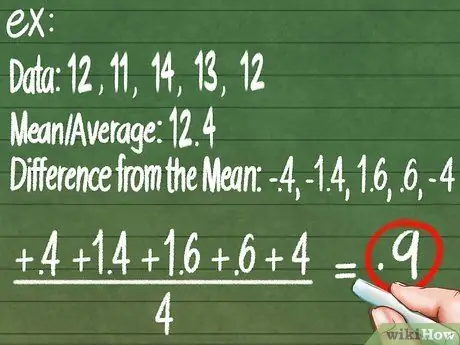
Step 5. Calculate the mean absolute deviation for more precise precision
Look again at our data mean: 12.4 kg. Subtract each measurement from the mean to find how far each measurement is from the data center. Make all negative numbers positive. For example:
Data:
12, 11, 14, 13, 12. Mean/Average:
12, 4
Difference from mean:
-0, 4; -1, 4; 1, 6; 0, 6; -0, 4"
. Now, find the average of these numbers to find how far the average of each measurement is from the center:
(0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4) / 5 = 0, 88. This means that in general any measurements you take can differ ±0.88 kg from what you see.
You must ignore the negative sign otherwise the values will cancel each other out. Keep in mind that 11, 4 and 13, 4 are both 1 kg difference from the average of 12, 4, only that the difference is opposite (positive or negative)
Tips
- If one of your test values is higher or lower than the others, do not exclude this number from your calculations. Even if this value is an error, it is data and should be used for correct calculations.
- Do more than 5 tries to get a more accurate calculation. The more experiments you do, the clearer the precision value you will get.
