- Author Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- Last modified 2025-01-23 12:04.
Displacement in physics denotes a change in the position of an object. When you calculate displacement, you calculate how far away an object is based on its initial and final locations. The formula you use to calculate displacement depends on the variable given to the problem. Follow these steps to calculate displacement.
Step
Part 1 of 5: Calculating the Resultant Displacement

Step 1. Use the resultant displacement formula if the unit of distance is used to indicate your starting and ending locations
Although distance is different from displacement, the resultant displacement problem looks for how many kilometers or meters the object has traveled. You'll use this unit of measurement to calculate displacement and how far away an object's location deviates from its starting point.
- The resultant displacement formula is written as: S = x²+y². S is displacement. X is the first direction of motion of the object and Y is the second direction of motion of the object. If your object only moves in one direction, then Y = 0.
- An object can only move in a maximum of two directions because moving along a north/south or east/west axis is considered neutral motion.

Step 2. Connect the dots in order of motion and label them from A-Z
Use a ruler to draw a straight line from point to point.
- Also remember to connect your starting point with your end point using a straight line. This is the displacement we will calculate.
- For example, if an object moves east 300 m and north 400 m, it will form a right triangle. AB will be the first leg of the triangle, and BC will be the second leg. AC will be the hypotenuse of the triangle and its magnitude is the displacement of the object. In this example, the two directions are east and north.

Step 3. Enter values for x² and y²
Now that you know the two directions of motion of your object, enter the values into the appropriate variables.
For example, x = 300 and y = 400. Your formula should look like this: S = 300² + 400²
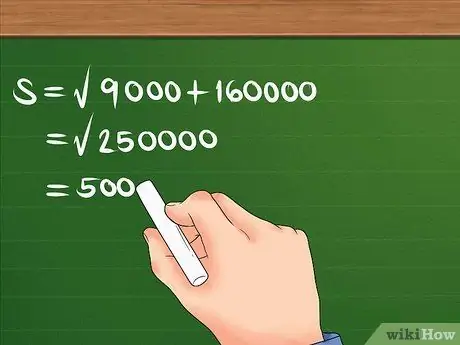
Step 4. Calculate the formula using the order of operations
Square 300 and 400 first, then add them up, and find the square root of the sum.
For example: S = 90000 + 160000. S = 250000. S = 500. Now you know that the displacement is 500 m
Part 2 of 5: When Speed and Time Are Known

Step 1. Use this formula when the problem tells you the speed of an object and the time it takes
Some math problems won't tell you how far or how fast an object is moving. You can calculate displacement using this magnitude of time and speed.
-
In this case, the formula becomes: S = 1/2(u + v)t.
U = initial velocity of the object, or how fast the object begins to move in a certain direction. V = the object's final velocity, or how fast the object is moving towards its final location. T = the time it takes the object to reach its final location.
- Example: A car goes down the road for 45 seconds (time required). The car is turning west at 20 m/s (initial speed) and at the end of the road, it is 23 m/s (final speed). Calculate the displacement based on these factors.

Step 2. Enter the required speed and time into the appropriate variables
Now that you know how far the car is moving, how fast the car is moving at the start and end, you can find the distance from the starting location to the final location.
Your formula should look like this: S = 1/2(20 + 23)45

Step 3. Calculate the formula after you put the values in the correct place
Remember to follow the order of operations, otherwise the displacements will result in very different values.
- For this formula, it doesn't matter if you accidentally swap the starting and ending speeds. Since you'll be adding these numbers together first, it doesn't matter where they are in parentheses. However, for other formulas, swapping the initial and final velocities will result in different displacement values.
- Your formula should look like this: S = 1/2(43)45. First divide 43 by 2, which results in 21, 5. Then multiply 21, 5 by 45, so the result is 967.5 meters. 967, 5 is the magnitude of your displacement, or how far your car has moved from its starting point.
Part 3 of 5: When the Initial Velocity, Acceleration, and Time are Known

Step 1. Use the modified formula when the acceleration is known in addition to the initial velocity and time
Some questions will only tell you how fast the object is moving at the beginning, how fast the object is starting to accelerate, and how far the object is moving. You will need the following formula.
- The formula for this problem is: S = ut + 1/2at². U still indicates the initial speed; a is the acceleration of the object, or how fast its velocity begins to change. T can mean the time it takes or a certain amount of time it takes an object to accelerate. Both will use time units such as seconds, hours, and others.
- Suppose a car moving at 25 m/s (initial velocity) begins to accelerate at 3 m/s2 (acceleration) for 4 seconds (time). What is the displacement of the car after 4 seconds?

Step 2. Enter the values in the formula
Unlike the previous formula, only the initial speed is represented here, so make sure to enter the correct data.
Based on the sample data above, your formula would look like this: S = 25(4) + 1/2(3)4². It helps to add parentheses around your acceleration magnitude and time to help you separate the numbers
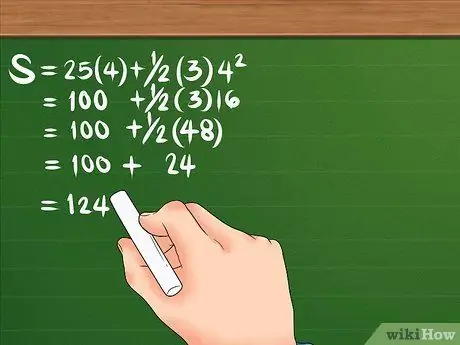
Step 3. Calculate the displacement by doing it in the correct order of operations
A quick way to help you remember the sequence of operations is the donkey bridge Kur ir Kua ci Kadang Ba wa Juragan Turtles. This represents the correct order: parentheses, squares, multiplication, division, addition, and subtraction.
Let's look at the formula again: S = 25(4) + 1/2(3)4². First, square 4, the result is 16. Then, multiply 16 by 3, making 48; then also multiply 25 by 4, to make 100. Divide 48 by 2, to make 24. Your equation should look like this: S = 100 + 24. Once you add the two together, the displacement is 124 meters
Part 4 of 5: Calculating Angular Displacement

Step 1. Find the angular displacement as the object moves in a circular path
Although you'll still be calculating displacement using a straight line, you'll need to find the difference between the object's starting and ending locations as it moves in a circular path.
- Imagine a girl sitting on a merry-go-round. As he spins with the carousel, he will move in a circular path. Angular displacement attempts to find the shortest distance between the initial and final locations when the object is not moving in a straight line.
- The formula for angular displacement is: = S/r, where S is the linear displacement, r is the radius, and is the angular displacement. Linear displacement is how far an object moves along an arc. The radius is the object's distance to the center of the circle. Angular displacement is the value we want to find.

Step 2. Plug the linear displacement and radius into the equation
Remember that the radius is the distance from the center of the circle; some problems will tell you the diameter of a circle, which must be divided by 2 to find the radius.
- Here is an example problem: A girl rides a merry-go-round. The seat is 1 meter from the center of the circle (the radius). If the girl is moving in an arc trajectory 1.5 meters (linear displacement), what is her angular displacement?
- Your equation will look like this: = 1.5/1.
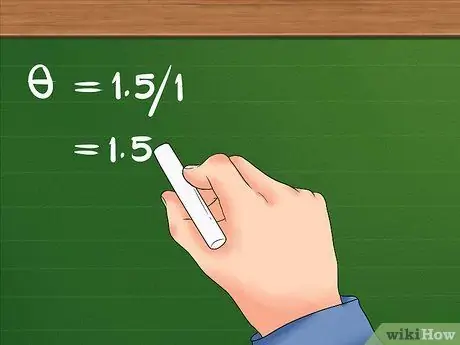
Step 3. Divide the linear displacement by the radius
This division will result in the angular displacement of the object.
- After dividing 1.5 by 1, the result is 1.5. The girl's angular displacement is 1.5 radians.
- Since angular displacement measures how much an object rotates from its initial position, it should be measured as an angle, not a distance. Radian is the unit used to measure angles.
Part 5 of 5: Understanding About Migration
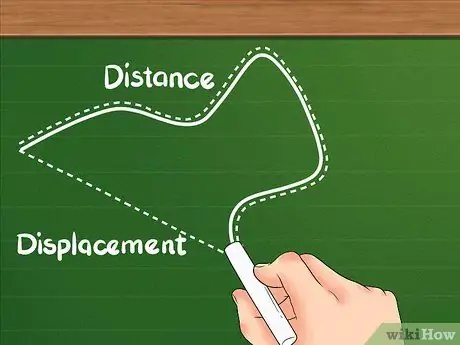
Step 1. Know that distance has a different definition than displacement
Distance shows how far the total distance traveled by the object.
- Distance is often known as a scalar quantity. Distance shows the distance traveled by an object regardless of the direction of the object.
- For example, if you walk 2 steps east, 2 steps south, 2 steps west, and then 2 steps north, you will return to your starting position. Even though you have gone through the total distance 10 steps away, you just move 0 steps away because your final location is the same as your starting location (your path resembles a box).

Step 2. Understand that displacement is the difference between two locations
Displacement is not the total sum of motion like distance; shifts focus on the area between your starting and ending locations.
- Displacement is called a vector quantity and shows the change in position of an object by considering the direction of motion of the object.
- For example, you walk east for 5 steps. If you go back west 5 steps, you will move in the opposite direction from your original location. Even though you've covered 10 steps, your position hasn't changed; your displacement is 0 steps.

Step 3. Remember the words forward and backward when trying to imagine displacement
Moving in the opposite direction eliminates the displacement of an object.
Imagine a football coach back and forth on the sidelines. As he shouted at the players, he shifted from left to right several times. If you watch it as it moves from left to right, you observe the total distance it has traveled. However, suppose the coach stops to talk to the quarterback on the sidelines. If he is at a different point than his initial location before moving, then you are observing the trainer move

Step 4. Know that displacement is measured using a straight path, not a circular path
To find displacement, you have to find the shortest and most efficient way to calculate the difference between two points.
- A circular path will take you from your starting location to your final location, but it's not the shortest path. To help you visualize it, imagine that you are walking in a straight line and you come across a pillar. You can't break through this pillar, so you go around it. Even though your final position is the same as if you broke through the pillar, you will need extra steps to reach that goal.
- Although displacement represents a straight path, know that you can measure the displacement of an object that is currently move in a circular path. This displacement is called angular displacement and can be calculated by finding the shortest path from the initial location to the final location.

Step 5. Know that displacement can be negative, unlike distance
If your final location is reached by moving in the opposite direction to your initial direction, then your displacement is negative.
- For example, we walk 5 steps east and then 3 steps west. Even though by calculation you move 2 steps from your starting location, your displacement is -2 because you are moving in the opposite direction. Your distance will always be positive because you can't count backwards in steps, kilometers, and so on.
- Negative displacement does not mean that displacement decreases. Negative just means the direction is opposite.

Step 6. Realize that sometimes distance and displacement can be the same
If you walk 25 steps straight and stop, the distance you travel will be equal to the displacement from your original location.
- This only applies when you move from one location from your starting location in a straight line. For example, you live in San Francisco, California, and get a new job in Las Vegas, Nevada. You have to move to Las Vegas to be close to your job. If you get on an airplane that flies straight from San Francisco to Las Vegas, you will travel the same distance and displacement x.
- However, if you drive from San Francisco to Las Vegas, you will travel a distance x, but travel a distance y. Since driving a car usually has variable directions (east of this road, west of that road), you'll be traveling longer distances than the shortest distance between the two cities.






