How to Calculate Lens Magnification: 12 Steps (with Pictures)

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-16 19:04

In studying optical instruments, the "magnification" of a lens-like object is the ratio of the height of the image you see to the actual height of the object. For example, a lens that can make an object look very large has a "high" magnification factor, while a lens that makes an object look small has a "low" magnification factor. The formula for the enlargement of an object is usually calculated using the formula M = (h_i/h_o) = -(d_i/d_o), where M = magnification, h_i = height of image, h_o = height of object, and d_i and D_o = distance of image and object.

Step

Method 1 of 2: Calculating Single Lens Magnification

Notes: A converging lens wider in the center than at the edges (like a magnifying glass). a divergent lens wider at the edges than in the center (like a bowl). Calculating the magnification on both lenses is the same, with one important exception. Click here to go directly to the exceptions to divergent lenses.

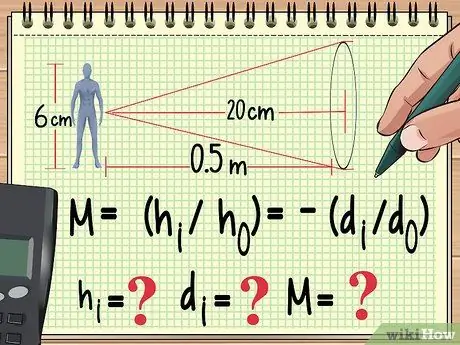
Step 1. Start with your equation and the variables you already know

Just like any other physics problem, the way to solve an enlargement problem is to write down the equation that you will use to calculate it. From here, you can work backwards to find the value of the variable you haven't found from the equation you're using.

• For example, suppose a 6 cm tall doll is placed one meter from a converging lens with a focal length of 20 cm. If we want to calculate the magnification, image height, and image distance, we can start writing our equation as follows:

  M = (h_i/h_o) = -(d_i/d_o)

• Now we know h_o (height of the doll) and d_o (doll distance from lens). We also know the focal length of the lens, which is not in this equation. We will count h_i, d_i, and M.

Step 2. Using the lens equation to get d_i.

If you know the distance from the object you are magnifying and the focal length of the lens, calculating the distance from the image formed is very easy with the lens equation. The equation of the lens is 1/f = 1/d_o + 1/d_i, where f = focal length of the lens.

• In this example problem, we can use the lens equation to calculate d_i. Enter the values of f and d_i then solve the equation:

  1/f = 1/d_o + 1/d_i

  1/20 = 1/50 + 1/d_i

  5/100 - 2/100 = 1/d_i

  3/100 = 1/d_i

  100/3 = d_i = 33.3 cm

• The focal length of the lens is the distance from the center of the lens to the point where light is transmitted at the focal point. If you've ever focused light with a magnifying glass on burning ants, you've seen it. In the questions in the lesson, usually the magnitude of this hotspot has been given. In real life, these specifications are usually written on a label located on the lens.

Step 3. Calculating h_i.

After you calculate d_o and D_i, you can calculate the height of the magnified object and the magnification of the lens. Notice the two equals signs in the lens magnification equation (M = (h_i/h_o) = -(d_i/d_o)) - this means that all parts of this equation are equal to each other, so we can calculate M and h_i in whatever order we want.

• For this example problem, we can calculate h_i like this:

  (h_i/h_o) = -(d_i/d_o)

  (h_i/6) = -(33, 3/50)

  h_i = -(33, 3/50) x 6

  h_i = -3, 996 cm

• Note that the height of the object here is negative which indicates that the image that we will see later will be inverted (top-bottom).

Step 4. Calculating M

You can calculate the last variable with the equation -(d_i/d_o) or (h_i/h_o).

• In the following example, how to calculate M is as follows:

  M = (h_i/h_o)

  M = (-3, 996/6) = -0, 666

• The result will also be the same when calculated using the value of d:

  M = -(d_i/d_o)

  M = -(33, 3/50) = -0, 666

• Note that the zoom does not have a unit label.

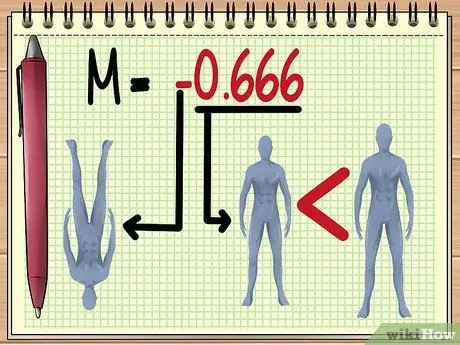
Step 5. Understanding the M value

Once you get the magnitude of the M value, you can estimate several things about the image you will see through the lens, namely:

• The size.

  The larger the "absolute value" of M, the larger the object viewed with the lens will appear. M value between 0 to 1 indicates that the object will look smaller.

• Object orientation.

  A negative value indicates that the image formed will be reversed.

• In the example given here, the M value of -0.666 means, according to the value of the existing variable, the shadow of the doll will be visible. upside down and two thirds smaller than the actual size.

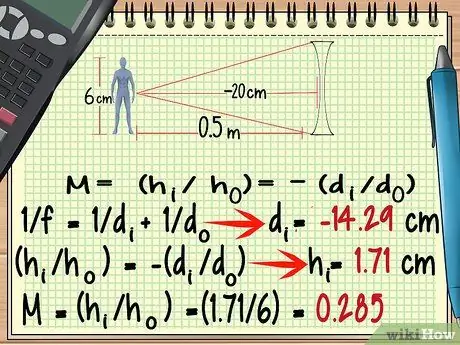
Step 6. For a diverging lens, use a negative focal point

Although the shape of a diverging lens is very different from that of a converging lens, you can calculate its magnification using the same formula as above. The exceptions to keep in mind are The focal point of the diverging lens is negative.

In the example problem above, this will affect the answer you will get in calculating d_i, so make sure you pay attention to this.

• Let's rework the example problem above, only now we use a diverging lens with focal length -20 cm.

  The other variables remain the same value.

• First of all, we will calculate d_i using the lens equation:

  1/f = 1/d_o + 1/d_i

  1/-20 = 1/50 + 1/d_i

  -5/100 - 2/100 = 1/d_i

  -7/100 = 1/d_i

  -100/7 = d_i = -14, 29 cm

• Now we will calculate h_i and M with a value of d_i the new one.

  (h_i/h_o) = -(d_i/d_o)

  (h_i/6) = -(-14, 29/50)

  h_i = -(-14, 29/50) x 6

  h_i = 1, 71 cm

  M = (h_i/h_o)

  M = (1, 71/6) = 0, 285

Method 2 of 2: Calculating the Magnification of Multiple Lenses

Simple Two Lens Method

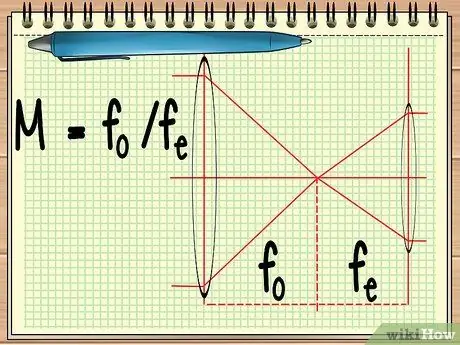
Step 1. Calculate the focal point of the two lenses

When you use an instrument that consists of two lenses arranged side by side (such as a telescope or a pair of binoculars), all you have to find out is the focal point of the two lenses to calculate the overall magnification of the two lenses. this can be calculated by the simple equation M = f_o/f_e.

In the equation, f_o is the focal point of the objective lens and f_e is the focal point of the eyepiece. The objective lens is the large lens that is close to the object, while the ocular lens is the lens that is located close to the observer's eye.

Step 2. Plug the information you already have into the equation M = f_o/f_e.

Once you have the focal points of both lenses, it is very easy to calculate them, - calculate the ratio by dividing the focal length of the objective lens by the focal length of the eyepiece. The answer you get is the total magnification of the tool.

• For example, suppose a simple telescope, it is written that the focal point of the objective lens is 10cm and the focal point of the eyepiece is 5cm, then the magnification is 10/5 = 2.

Complicated Method

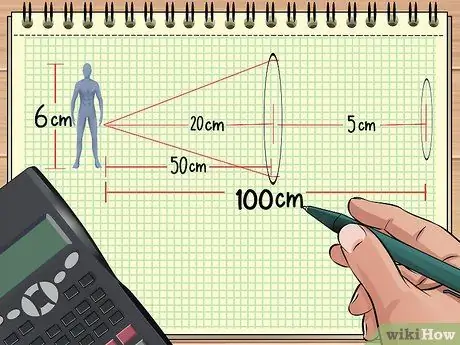
Step 1. Calculate the distance between the lenses and the object

If you have two lenses arranged in a row in front of an object, the total magnification can be calculated if you know the distance from the lenses to the object, the size of the object, and the focal point of the two lenses. The remainder can also be calculated.

For example, suppose we arrange objects and lenses as in the example problem 1 above: a doll is 50 cm from a converging lens that has a focal length of 20 cm. Now, place the second lens with focal point 5 cm at a distance of 50 cm from the first lens (100 cm from the doll.) After this, we will calculate the total magnification using the information we have obtained

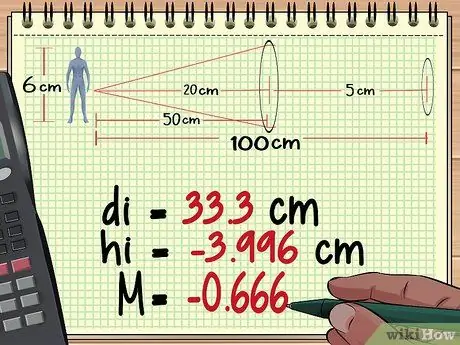
Step 2. Calculate the object distance, height, and magnification from lens 1

The first part of calculating the magnification of multiple lenses is the same as calculating the magnification of a single lens. Start with the lens closest to the object, use the lens equation to find the distance from the image formed, then use the magnification equation to find the image's height and magnification. Click here to view more single lens magnification calculations.

• From our calculations in Method 1 above, we find that the first lens produces an image as high as -3, 996 cm, distance 33.3 cm behind the lens, and at a magnification of -0, 666.

Step 3. Use the image from the first lens as the object from the second lens

Now, finding the magnification, height and more for the second lens is very easy - just use the same method you used for the first lens, only, this time treat the image as an object. Remember that the image distance to the second lens is not always the same as the object distance to the first lens.

• In the example above, since the image is formed 33.3 cm behind the first lens, the distance is 50-33.3 = 16.7 cm in front of the second lens. Let's use this measurement and the focal length of the second lens to find the image formed by the second lens.

  1/f = 1/d_o + 1/d_i

  1/5 = 1/16, 7 + 1/d_i

  0, 2 - 0, 0599 = 1/d_i

  0, 14 = 1/d_i

  d_i = 7, 14 cm

• Now we can calculate h_i and M for the second lens:

  (h_i/h_o) = -(d_i/d_o)

  (h_i/-3, 996) = -(7, 14/16, 7)

  h_i = -(0, 427) x -3, 996

  h_i = 1, 71 cm

  M = (h_i/h_o)

  M = (1, 71/-3, 996) = -0, 428

Step 4. Continue calculating like this for the additional lenses

This basic approach is the same if there are three, four, or hundreds of lenses lined up in front of an object. For each lens, consider the image of the previous lens as the object and use the lens equation and the magnification equation to find the answer you want.

Keep in mind that each subsequent lens can continuously invert the image formed. For example, the magnification value we obtained earlier (-0, 428) indicates that the image we are going to see is approximately 4/10 of the actual object size, but perpendicular, because the image from the previous lens is inverted

Tips

• Binoculars usually provide an explanation of the magnification specifications in the form of a number times another number. For example, binoculars can be specified as 8x25 or 8x40. When written like that, the first number is the magnification of the binoculars. It doesn't matter even if in the example given, the two numbers are different in magnitude, both binoculars have a magnification of 8 times. The second number indicates how clear the image will be formed by the binoculars.
• Remember that for single-lens loupe, the magnification will be negative if the object distance is greater than the focal length of the lens. This does not mean that the image formed will be smaller. In this case, the enlargement still occurs, but the image formed will be seen upside down (top-down) by the observer.