- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
The radius of the sphere (abbreviated using the variable r or R) is the distance from the center of the sphere to a point on its surface. Like a circle, the radius of a sphere is an important part of the initial information needed to calculate the diameter, circumference, surface area and/or volume of a sphere. However, you can also reverse the calculations of diameter, circumference, etc., to find the radius of the sphere. Use the formula according to the information you have.
Step
Method 1 of 3: Using the Radius Formula
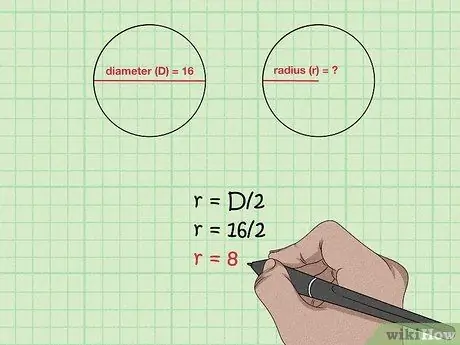
Step 1. Find the radius if the diameter is known
The radius is half the diameter, so use the formula r = D/2. This formula is exactly the same as calculating the radius of a circle from its diameter.
-
So, if a ball has a diameter of 16 cm, the radius can be calculated as 16/2, which is 8 cm. If the diameter is 42, the radius is
Step 21..
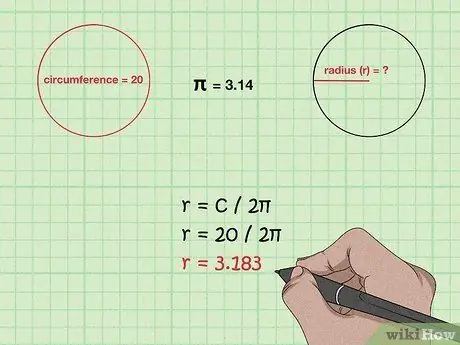
Step 2. Find the radius if the perimeter is known
Use formula C/2π. Since the perimeter is D, which is also 2πr, divide the circumference by 2π to get the radius.
- If a sphere has a circumference of 20 m, its radius can be found from 20/2π = 3, 183 m.
- Use the same formula to convert between the radius and circumference of a circle.

Step 3. Calculate the radius if the volume of the sphere is known
Use the formula ((V/π)(3/4))1/3. The volume of the sphere is derived from the formula V = (4/3)πr3. Solve the variable r in this equation to be ((V/π)(3/4))1/3 = r, meaning that the radius of the sphere is equal to the volume divided by, multiplied by 3/4, then all to the power of 1/3 (or equal to the square root of 3.)
-
If a sphere has a volume of 100 inches3, the solution is as follows:
- ((V/π)(3/4))1/3 = r
- ((100/π)(3/4))1/3 = r
- ((31, 83)(3/4))1/3 = r
- (23, 87)1/3 = r
- 2.88 inches = r
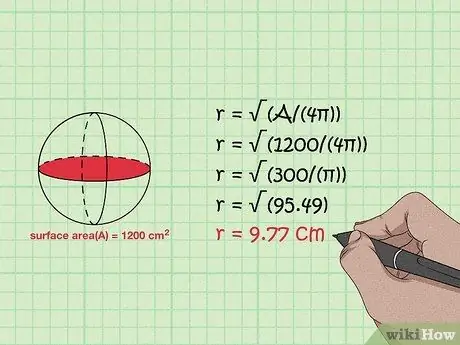
Step 4. Find the radius using the surface area
Use formula r = (A/(4π)). The surface area of a sphere is derived from the formula A = 4πr2. Solve the variable r to get (A/(4π)) = r, meaning that the radius of a sphere is equal to the square root of the surface area divided by 4π. The result can also be obtained by raising (A/(4π)) by 1/2.
-
If a sphere has a surface area of 1200 cm2, the solution is as follows:
- (A/(4π)) = r
- (1200/(4π)) = r
- (300/(π)) = r
- (95, 49) = r
- 9, 77 cm = r
Method 2 of 3: Defining Some Key Concepts

Step 1. Identify some of the basic sizes of a ball
Fingers (r) is the distance from the center of a sphere to any point on its surface. In general, you can find the radius of a sphere if you know its diameter, circumference, volume, and surface area.
- Diameter (D): center line of a sphere-radius multiplied by two. Diameter is a line that passes through the center of the sphere from one point on the surface of the sphere to another point on the surface of the sphere directly opposite it. In other words, the diameter is the furthest distance between two points on a sphere.
- Circumference (C): the farthest distance around the surface of the sphere. In other words, it is equal to the circumference of the cross section of the sphere through the center of the sphere.
- Volume (V): fill the three-dimensional space inside a sphere. Volume is "the space occupied by a sphere."
- Surface area (A): the area of two dimensions on the surface of the sphere. Surface area is the area that covers the entire surface of the sphere.
- Pi (π): a constant which is the ratio of the circumference and the diameter of the circle. The first ten digits of Pi are 3, 141592653, usually rounded up to 3, 14 only.

Step 2. Use various measurements to find the radius
You can use the diameter, circumference, and surface area to calculate the radius of a sphere. You can also calculate all of these dimensions if you know the radius of the sphere. So, to find the radius, try reversing the following formulas. Learn the formulas that use the radius to find diameter, circumference, volume, and surface area.
- D = 2r. As with a circle, the diameter of the sphere is twice the radius.
- C = D or 2πr. As with a circle, the circumference of a sphere is times the diameter. Since the diameter is twice the radius, we can say that the circumference is twice the radius times.
- V = (4/3)πr3. The volume of a sphere is the radius of the cube (multiplied by itself twice), times, times 4/3.
- A = 4πr2. The surface area of a sphere is the radius squared (multiplied by itself), times, times 4. Since the area of a circle is r2, it can be said that the surface area of a circle is four times the area of the circle that forms its circumference.
Method 3 of 3: Finding the Radius as the Distance Between Two Points
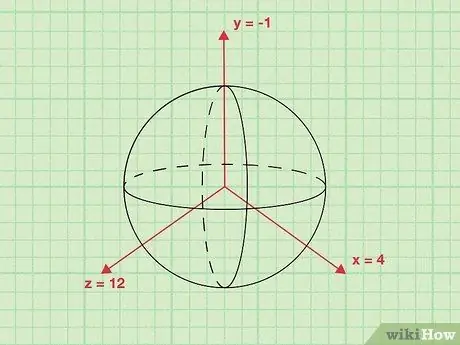
Step 1. Find the coordinates (x, y, z) of the center of the sphere
One way of looking at the radius of a sphere is as the distance between the center and any point on the surface of the sphere. Since this statement is true, if we know the coordinates of the center of the sphere and any point on its surface, we can find the radius of the sphere by calculating the distance between two points using a variation of the usual distance formula. To begin with, the way the coordinates of the center point. Note that a sphere is a three-dimensional object, so its coordinates are (x, y, z) rather than (x, y) only.
This process is easy to understand by following an example. For example, suppose there is a sphere whose center in coordinates (x, y, z) is (4, -1, 12). With a few steps, we will use this point to find the radius.

Step 2. Find the coordinates of the point on the surface of the sphere
Next, find the (x, y, z) coordinates of the point on the surface of the sphere. This point can be taken from any position on the surface of the sphere. Since the points on the surface of a sphere are equidistant from the center by definition, any point can be used to determine the radius.
For example, suppose we know the point (3, 3, 0) lies on the surface of the sphere. By calculating the distance between this point and the center, we can get the radius.

Step 3. Find the radius with the formula d = ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2).
Now that you know the center of the sphere and a point on the surface, you can calculate the distance between them to find the radius. Use the formula for distance in three dimensions d = ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2); d is the distance, (x1, y1, z1) are the coordinates of the center point, and (x2, y2, z2) is the coordinate of a point on the surface that is used to determine the distance between the two points.
-
From the example, enter the number (4, -1, 12) in (x1, y1, z1) and (3, 3, 0) on (x2, y2, z2), and solve as follows:
- d = ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
- d = ((3 - 4)2 + (3 - -1)2 + (0 - 12)2)
- d = ((-1)2 + (4)2 + (-12)2)
- d = (1 + 16 + 144)
- d = (161)
- d = 12, 69. This is the radius of the sphere we are looking for.
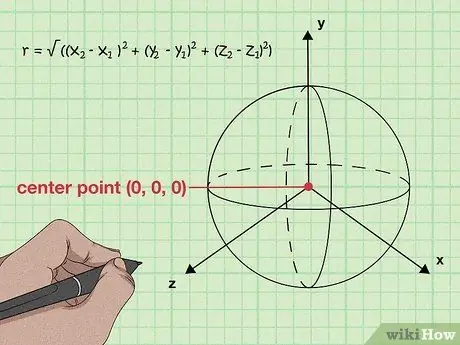
Step 4. Know as a general equation r = ((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2).
On a sphere, every point on its surface is the same distance from the center. If we use the distance formula above and replace the variable "d" with the variable "r" for the radius, we will get the form of the equation for finding the radius if we know the center point (x1, y1, z1) and another point on the surface (x2, y2, z2).
By squaring both sides of the equation, we get r2 = (x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2. Note that this formula is essentially the same as the basic spherical equation r2 = x2 + y2 + z2 with the center point (0, 0, 0).
Tips
- The order of operations in the formula matters. If you don't know the exact order in which you're working but you have a calculator with brackets on it, just use it.
- This article was written on request. However, if you are trying to understand the geometry of space for the first time, it is better to start from scratch: calculating the dimensions of a sphere from the radius.
- If you can measure a sphere in real life, one way to get the size is to use water. First, estimate the size of the ball in question so that it can be immersed in a container of water and collect the overflowing water. Then measure the volume of water that overflows. Convert from mL to cubic centimeters or any other desired unit, and use this number to find r with the equation v=4/3*Pi*r^3. This process is a little more complicated than measuring the circumference using a tape measure or ruler, but it can be more accurate because you don't have to worry about missing the size because it's not centered.
- or Pi is the Greek alphabet that represents the ratio of the diameter to the circumference of a circle. This constant is an irrational number that cannot be written in the ratio of integers. There are some shards that can come close; 333/106 can approximate Pi to four decimal places. Today, people generally use rounding 3, 14, which is usually sufficient for everyday purposes.






