- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Rational expressions must be simplified down to the same simplest factors. This is a fairly easy process if the same factor is a single term factor, but it gets a little more detailed if the factor includes many terms. Here's what you should do, depending on the type of rational expression you're dealing with.
Step
Method 1 of 3: Mononomial Rational Expressions (Single Term)

Step 1. Check the problem
Rational expressions that only consist of monomials (single terms) are the easiest expressions to simplify. If both terms in the expression have only one term, all you have to do is simply simplify the numerator and denominator to the same lowest terms.
- Note that mono means “one” or “single” in this context.
-
Example:
4x/8x^2

Step 2. Eliminate any variables that are the same
Look at the letter variables in the expression. If the same variable appears in both the numerator and denominator, you can omit this variable as many times as it appears in both parts of the expression.
- In other words, if the variable occurs only once in the expression in the numerator and once in the denominator, the variable can be completely omitted: x/x = 1/1 = 1
- However, if a variable occurs multiple times in both the numerator and denominator, but only occurs at least once in another part of the expression, subtract the exponent that the variable has in the smaller part of the expression from the exponent that the variable has in the larger part: x^4/ x^2 = x^2/1
-
Example:
x/x^2 = 1/x
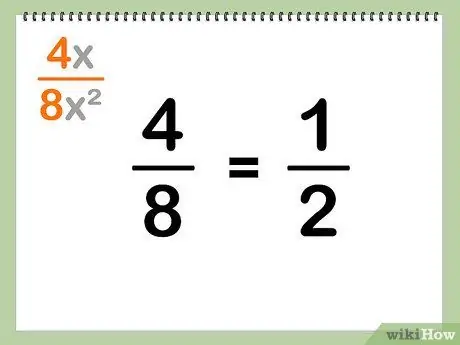
Step 3. Simplify the constants to their simplest terms
If the constants of a number have the same factors, divide the constant in the numerator and the constant in the denominator by the same factor, to simplify the fraction to its simplest form: 8/12 = 2/3
- If the constants in a rational expression do not have the same factors, then they cannot be simplified: 7/5
- If one constant is divisible by another constant, then it is considered an equal factor: 3/6 = 1/2
-
Example:
4/8 = 1/2

Step 4. Write down your final answer
To determine your final answer, you must again combine the simplified variables and simplified constants.
-
Example:
4x/8x^2 = 1/2x
Method 2 of 3: Binomial and Polynomial Rational Expressions with Mononomial Factors (Single Term)

Step 1. Check the problem
If one part of a rational expression is a monomial (single term), but the other part is a binomial or polynomial, you may need to simplify the expression by specifying a monomial (single term) factor that can be applied to both the numerator and denominator.
- In this context, mono means “one” or “single”, bi means “two”, and poly means “many”.
-
Example:
(3x)/(3x + 6x^2)
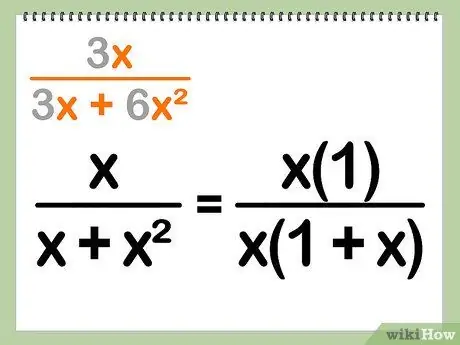
Step 2. Spread out any variables that are the same
If any letter variable appears in all terms of the equation, you can include that variable as part of the factored out term.
- This only applies if the variable occurs in all terms of the equation: x/x^3 - x^2 + x = (x)(x^2 - x + 1)
- If one of the terms of the equation doesn't have this variable, you can't factor it out: x/x^2 + 1
-
Example:
x/(x + x^2) = [(x)(1)] / [(x)(1 + x)]

Step 3. Spread out any constants that are the same
If the numeric constants in all terms have the same factors, divide each constant in the terms by the same factor, to simplify the numerator and denominator.
- If one constant is divisible by another constant, then it is considered an equal factor: 2 / (2 + 4) = 2 * [1 / (1 + 2)]
- Note that this only applies if all terms in the expression have at least one factor in common: 9 / (6 - 12) = 3 * [3 / (2 - 4)]
- This does not apply if any of the terms in the expression do not have the same factor: 5 / (7 + 3)
-
Example:
3/(3 + 6) = [(3)(1)] / [(3)(1 + 2)]

Step 4. Factor out the equal elements
Recombine the simplified variables and simplified constants to determine the same factor. Remove this factor from the expression, leaving variables and constants that are not the same in all terms.
-
Example:
(3x)/(3x + 6x^2) = [(3x)(1)] / [(3x)(1 + 2x)]

Step 5. Write down your final answer
To determine the final answer, remove the common factors from the expression.
-
Example:
[(3x)(1)] / [(3x)(1 + 2x)] = 1/(1 + 2x)
Method 3 of 3: Binomial or Polynomial Rational Expressions with Binomial Factors

Step 1. Check the problem
If there is no monomial term (single term) in the rational expression, you must break the numerator and fraction into binomial factors.
- In this context, mono means “one” or “single”, bi means “two”, and poly means “many”.
-
Example:
(x^2 - 4) / (x^2 - 2x - 8)

Step 2. Break down the numerator into its binomial factors
To break the numerator into its factors, you must determine the possible solutions for your variable, x.
-
Example:
(x^2 - 4) = (x - 2) * (x + 2)
- To find the value of x, you must move the constant to one side and the variable to the other: x^2 = 4
- Simplify x to the power of one by finding the square root of both sides: x^2 = 4
- Remember that the square root of any number can be positive or negative. Thus, the possible answers for x are: -2, +2
- Thus, when describing (x^2 - 4) being the factors, the factors are: (x - 2) * (x + 2)
-
Double-check your factors by multiplying them. If you are not sure that you have factored part of this rational expression correctly or not, you can multiply these factors to make sure that the result is the same as the original expression. Remember to use PLDT if appropriate to use: pfirst, loutside, dnatural, tend.
-
Example:
(x - 2) * (x + 2) = x^2 + 2x - 2x - 4 = x^2 - 4
-

Step 3. Break down the denominator into its binomial factors
To break the denominator into its factors, you must determine the possible solutions for your variable, x.
-
Example:
(x^2 - 2x - 8) = (x + 2) * (x - 4)
- To find the value of x, you must move the constant to one side and move all terms, including the variables, to the other side: x^2 2x = 8
- Complete the square of the coefficients of the x term and add the values to both sides: x^2 2x + 1 = 8 + 1
- Simplify the right side and write the perfect square on the right: (x 1)^2 = 9
- Find the square root of both sides: x 1 = ±√9
- Find the value of x: x = 1 ±√9
- Like any quadratic equation, x has two possible solutions.
- x = 1 - 3 = -2
- x = 1 + 3 = 4
- Therefore, (x^2 - 2x - 8) factored into (x + 2) * (x - 4)
-
Double-check your factors by multiplying them. If you are not sure that you have factored part of this rational expression correctly or not, you can multiply these factors to make sure that the result is the same as the original expression. Remember to use PLDT if appropriate to use: pfirst, loutside, dnatural, tend.
-
Example:
(x + 2) * (x - 4) = x^2 - 4x + 2x - 8 = x^2 - 2x - 8
-
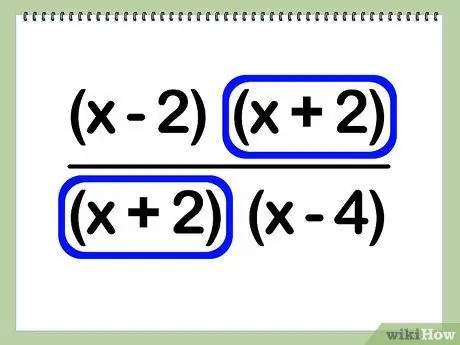
Step 4. Eliminate the same factors
Find the binomial factor, if any, that is the same in both the numerator and denominator. Remove this factor from the expression, leaving the binomial factors unequal.
-
Example:
[(x - 2)(x + 2)] / [(x + 2)(x - 4)] = (x + 2) * [(x - 2) / (x - 4)]
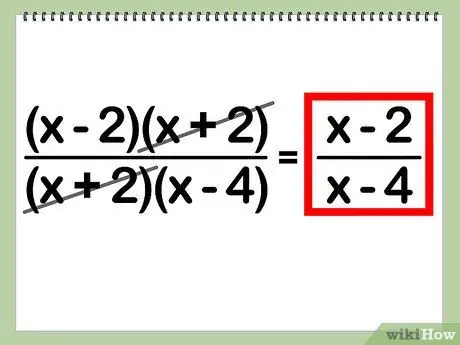
Step 5. Write down your final answer
To determine the final answer, remove the common factors from the expression.
-
Example:
(x + 2) * [(x - 2) / (x - 4)] = (x - 2) / (x - 4)






