- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Learning how to simplify algebraic expressions is one of the keys to mastering basic algebra and the most useful tool any mathematician needs to have. Simplification allows mathematicians to convert complex, long, and/or odd expressions into simpler or easier equivalent expressions. Basic simplification skills are easy to learn - even for those who hate math. By following a few simple steps, it is possible to simplify many of the most frequently used types of algebraic expressions, without using any special knowledge of mathematics. Check out Step 1 to get started!
Step
Understanding Important Concepts

Step 1. Group like terms based on the variables and their powers
In algebra, like terms have the same variable configuration, with the same power. In other words, for two terms to be equal, they must have the same variable, or no variable at all, and each variable has the same power, or no exponent. The order of the variables in terms is not important.
For example, 3x2 and 4x2 are like terms because they both have a variable x with the power of the square. However, x and x2 are not like terms because each term has a variable x with a different power. Almost the same, -3yx and 5xz are not like terms because each term has a different variable.

Step 2. Factor by writing the number as the product of the two factors
Factoring is the concept of writing down a given number as the product of two factors being multiplied. Numbers can have more than one set of factors - for example, 12 can be obtained from 1 × 12, 2 × 6, and 3 × 4, so we can say that 1, 2, 3, 4, 6, and 12 are factors of 12 Another way of imagining it is that the factors of a number are the numbers that divide the number whole.
- For example, if we wanted to factor 20, we could write it as 4 × 5.
- Note that variable terms can also be factored. -20x, for example, can be written as 4(5x).
- Prime numbers cannot be factored because they can only be divided by themselves and 1.

Step 3. Use the acronym KaPaK BoTaK to remember the order of operations
Sometimes, simplifying an expression simply solves the operation in the equation until it's no longer workable. In these cases, it is very important to remember the order of operations so that no arithmetic errors occur. The acronym KaPaK BoTaK will help you remember the order of operations - the letters indicate the types of operations you should perform, in the order:
- Kfail
- Plift
- Kali
- Bagain
- Tadd
- Kshrimp
Method 1 of 3: Merge Like-Terms
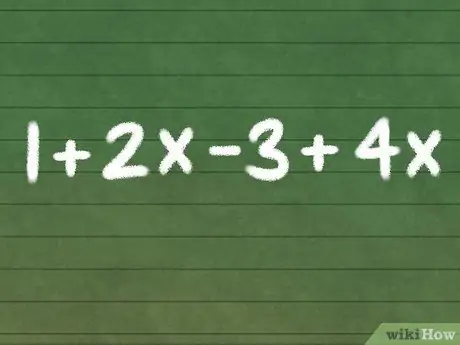
Step 1. Write down your equation
The simplest algebraic equations, involving only a few variable terms with integer coefficients and no fractions, roots, etc., can often be solved in just a few steps. For most math problems, the first step to simplifying your equation is to write it down!
As an example problem, for the next few steps, we use the expression 1 + 2x - 3 + 4x.
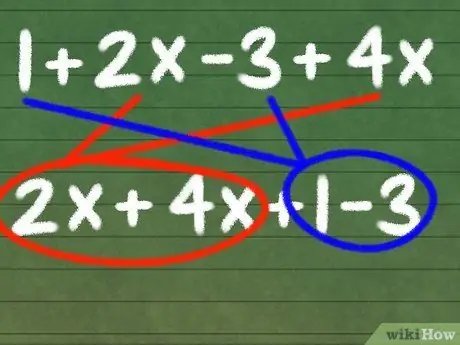
Step 2. Identify similar tribes
Next, look for like terms in your equation. Remember that like terms have the same variable and exponent.
For example, let's identify like terms in our equation 1 + 2x - 3 + 4x. 2x and 4x both have the same variable with the same power (in this case, x has no exponent). Also, 1 and -3 are like terms because they have no variables. So in our equation, 2x and 4x and 1 and -3 are similar tribes.
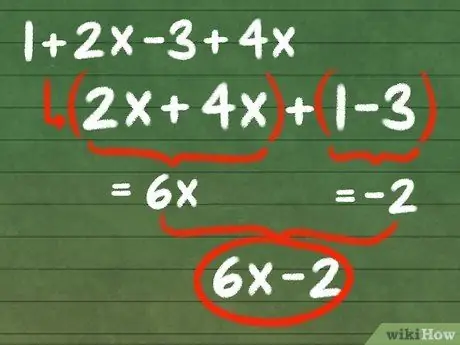
Step 3. Combine like terms
Now that you've identified like terms, you can combine them to simplify your equation. Add the terms (or subtract in the case of negative terms) to reduce the set of terms with the same variable and exponent to one equal term.
-
Let's add like terms in our example.
- 2x + 4x = 6x
- 1 + -3 = -2
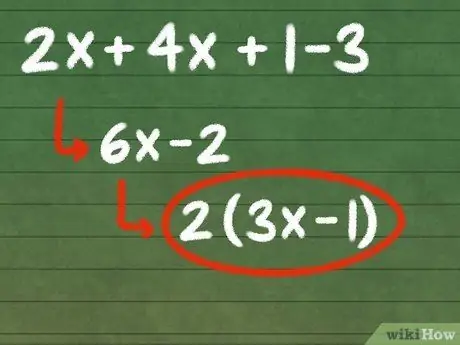
Step 4. Create a simpler equation from the simplified terms
After combining your like terms, make an equation from the new, smaller set of terms. You'll get a simpler equation, which has one term for the different sets of variables and powers in the original equation. This new equation is equivalent to the original equation.
In our example, our simplified terms are 6x and -2, so our new equation is 6x - 2. This simple equation is equivalent to the original (1 + 2x - 3 + 4x), but shorter and easier to work with. It's also easier to factor, which we'll look at below, which is another important simplifying skill.
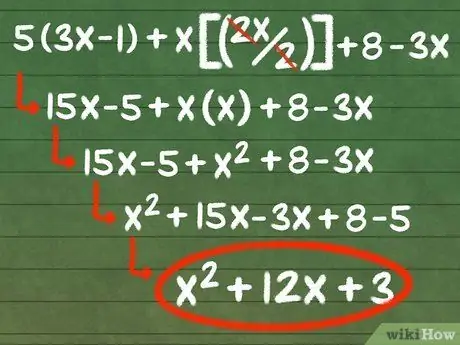
Step 5. Follow the order of operations when combining like terms
In very simple equations like the one we worked on in the example problem above, identifying like terms is easy. However, in more complex equations, such as expressions involving parenthetical terms, fractions, and roots, like terms that can be combined may not be clearly visible. In these cases, follow the order of operations, performing operations on the terms in your expression as needed until the addition and subtraction operations remain.
-
For example, we use the equation 5(3x-1) + x((2x)/(2)) + 8 - 3x. It would be wrong to immediately consider 3x and 2x as like terms and combine them because the parentheses in the expression indicate that we have to do other operations first. First, we perform the arithmetic operations on the expression in the order of operations to get terms that we can use. See the following:
- 5(3x-1) + x((2x)/(2)) + 8 - 3x
- 15x - 5 + x(x) + 8 - 3x
- 15x - 5 + x2 + 8 - 3x. Now, since the only remaining operations are addition and subtraction, we can combine like terms.
- x2 + (15x - 3x) + (8 - 5)
- x2 + 12x + 3
Method 2 of 3: Factoring
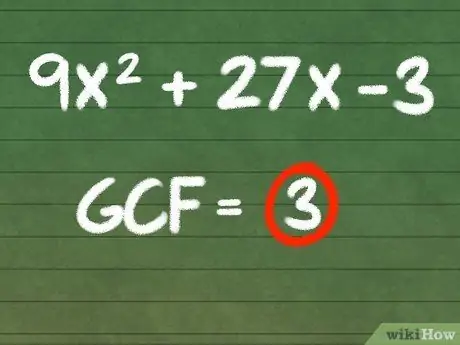
Step 1. Identify the greatest common factor in the expression
Factoring is a way to simplify an expression by removing the factors that are the same in all like terms in the expression. To start, find the greatest common factor that all the terms have - in other words, the largest number that divides all the terms in the expression whole.
-
Let's use the 9x. equation2 + 27x - 3. Notice that every term in this equation is divisible by 3. Since the terms are not divisible by any larger number, we can say that
Step 3. is our greatest common factor.
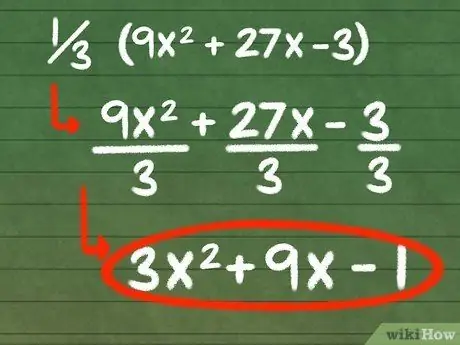
Step 2. Divide the terms in the expression by the greatest common factor
Next, divide each term in your equation by the greatest common factor you just found. The quotient terms will have a smaller coefficient than the original equation.
-
Let's factor our equation by its greatest common factor, 3. To do this, we'll divide each term by 3.
- 9x2/3 = 3x2
- 27x/3 = 9x
- -3/3 = -1
- Thus, our new expression is 3x2 + 9x - 1.
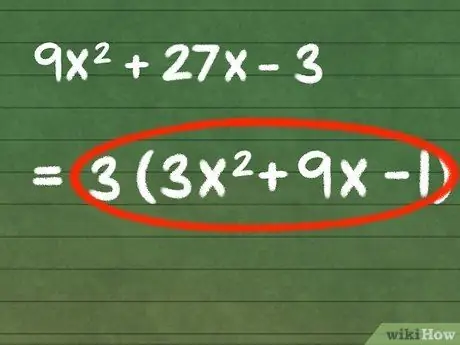
Step 3. Write your expression as the product of the greatest common factor multiplied by the remaining terms
Your new expression is not equivalent to your original expression, so it would be incorrect to say that the expression has been simplified. To make our new expression equal to the original, we must include the fact that our expression has been divided by the greatest common factor. Enclose your new expression in parentheses and write the greatest common factor of the original equation as the expression coefficient in parentheses.
For our example equation, 3x2 + 9x - 1, we can enclose the expression in parentheses and multiply it by the greatest common factor of the original equation to get 3(3x2 + 9x - 1). This equation is equivalent to the original equation, 9x2 +27x - 3.
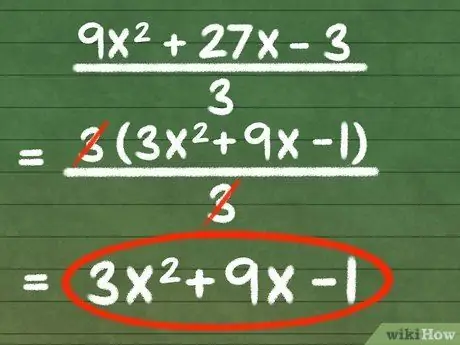
Step 4. Use factoring to simplify fractions
You may now be wondering why factoring is used, if even after removing the greatest common factor the new expression has to be multiplied again by that factor. In fact, factoring allows mathematicians to perform various tricks to simplify expressions. One of his easiest tricks takes advantage of the fact that multiplying the numerator and denominator of a fraction by the same number can produce equivalent fractions. See the following:
-
Say our initial example expression, 9x2 + 27x - 3, is the quantifier of the larger fraction with 3 as the numerator. The fraction will look like this: (9x2 + 27x - 3)/3. We can use factoring to simplify fractions.
- Let's substitute the factoring form of our original expression for the expression in the numerator: (3(3x2 + 9x - 1))/3
- Notice that now, both the numerator and denominator have a coefficient of 3. Dividing the numerator and denominator by 3, we get: (3x2 + 9x - 1)/1.
- Since any fraction with a denominator of 1 is equivalent to the terms in the numerator, we can say that our initial fraction can be simplified to 3x2 + 9x - 1.
Method 3 of 3: Applying Additional Simplification Skills
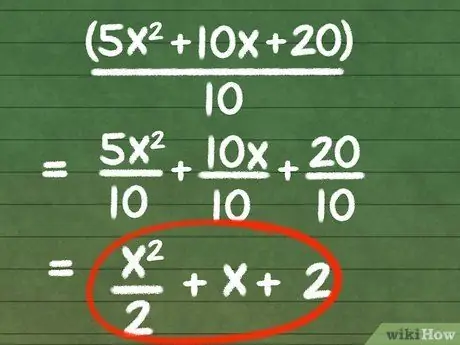
Step 1. Simplify fractions by dividing by the same factors
As noted above, if the numerator and denominator of an equation have the same factors, these factors can be completely omitted in the fraction. Sometimes, it will require factoring in the quantifier, denominator, or both (as is the case in the example problem above) while sometimes the same factors are often obvious. Note that it is also possible to divide the terms of the numerator by the equation in the denominator one by one to get a simple expression.
-
Let's work on an example that doesn't require factoring out. For fractions (5x2 + 10x + 20)/10, we can divide each term in the numerator by 10 to simplify, even if the coefficient is 5 in 5x2 is not greater than 10 and thus 10 is not a factor.
If we do, we will get ((5x2)/10) + x + 2. If we wanted, we could rewrite the first term as (1/2)x2 so we get (1/2)x2 +x+2.

Step 2. Use the squared factors to simplify the roots
The expression under the root sign is called the root expression. This expression can be simplified by identifying the squared factors (factors that are squares of integers) and performing the square root operation separately to remove them from under the square root sign.
-
Let's do a simple example - (90). If we think of 90 as the product of its two factors, 9 and 10, we can take the square root of 9 which is the integer 3 and remove it from the radical sign. In other words:
- √(90)
- √(9 × 10)
- (√(9) × √(10))
- 3 × √(10)
- 3√(10)
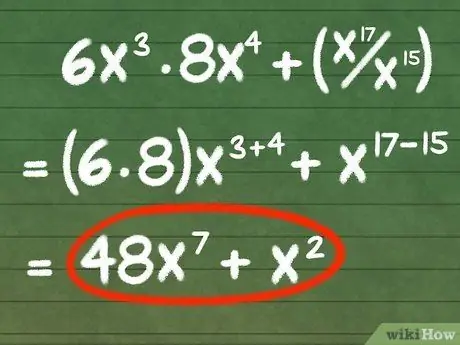
Step 3. Add exponents when multiplying two exponents; subtract when dividing
Some algebraic expressions require multiplication or division of power terms. Instead of calculating or dividing each exponent manually, just add the exponents when multiplying and subtract when dividing to save time. This concept can also be used to simplify variable expressions.
-
For example, let's use the expression 6x3 × 8x4 + (x17/x15). In any event where multiplication or division of exponents is required, we will subtract or add exponents, respectively, to quickly find the simple term. See the following:
- 6x3 × 8x4 + (x17/x15)
- (6 × 8)x3 + 4 + (x17 - 15)
- 48x7 +x2
-
For an explanation of how it works, see below:
- Multiplying terms in exponents is actually like multiplying terms not in long exponents. For example, because x3 = x × x × x and x 5 = x × x × x × x × x, x3 × x5 = (x × x × x) × (x × x × x × x × x), or x8.
- Almost the same, dividing the terms exponents like dividing the terms not a long exponent. x5/x3 = (x × x × x × x × x)/(x × x × x). Since each term in the numerator can be crossed out by finding the same term in the denominator, there are only two x's left in the numerator and nothing left at the bottom, giving the answer x2.
Tips
- Always remember that you have to imagine these numbers as having positive and negative signs. Many people stop to think about what Sign should I put here?
- Ask for help if you need it!
- Simplifying Algebraic Expressions is not easy, but once you understand it, you will use it for the rest of your life.
Warning
- Always look for similar tribes and don't be fooled by rank.
- Make sure you don't add numbers, exponents, or operations that shouldn't be there by accident.






