- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Algebraic fractions may seem difficult and intimidating to the uninitiated student. Algebraic fractions are made up of a mixture of variables, numbers, and even exponents so they can be confusing. Fortunately, however, the rules for simplifying common fractions, such as 15/25, also apply to algebraic fractions.
Step
Method 1 of 3: Simplifying Fractions

Step 1. Know the various terms in algebraic fractions
The following terms are often used in algebraic fraction problems:
-
Numerator:
the top of the fraction (example: '''(x+5)'''/(2x+3)).
-
Denominator:
the bottom of the fraction (example: (x+5)/'''(2x+3)''').
-
Common denominator:
a number that can divide the top and bottom of a fraction. Example: the common denominator of the fraction 3/9 is 3 because 3 and 9 are divisible by 3.
-
Factor:
numbers that can divide a number until it runs out. Example: factor 15 is 1, 3, 5, and 15. Factor 4 is 1, 2, and 4.
-
The simplest fraction:
take all the common factors and put the same variables together (5x + x = 6x) until you get the simplest problem, equation, or fraction. If there are no more calculations that can be done, the fraction is at its simplest.
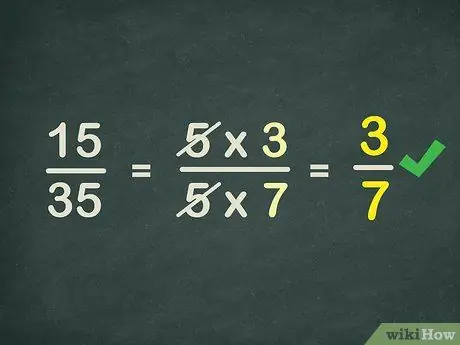
Step 2. Re-learn how to simplify common fractions
Algebraic fractions are simplified in the same way that they simplify ordinary fractions. For example, to simplify 15/35, find common denominator the fraction. The common denominator of the fraction 15/35 is 5. So, factor out 5 from the fraction
15 → 5 * 3
35 → 5 * 7
Now, remove common denominator. In the example above, remove both 5s. So, the simple form 15/35 is 3/7.

Step 3. Take the common factors out of algebraic expressions in the same way as for ordinary numbers
In the previous example, 5 can easily be factored out of 15. The same principle applies to more complex expressions, such as 15x - 5. Find the common factor of the two numbers in the problem. 5 is a common factor that can divide both 15x and -5. As before, take out the common factors and multiply by “the remainder”.
15x - 5 = 5 * (3x - 1) Check by multiplying 5 by the new expression. If it is correct, the result is the same as the original expression (before the common factor, which is 5, is excluded).
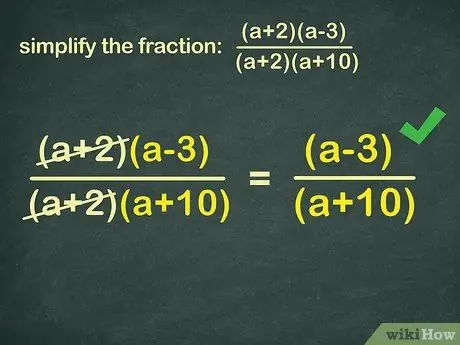
Step 4. In addition to common factors in the form of ordinary numbers, complex numbers can also be omitted
Algebraic fraction simplification uses the same principles as ordinary fractions. This principle is the easiest way to simplify fractions. Example:
(x+2)(x-3)
(x+2)(x+10)
exists in the numerator (top of the fraction) and denominator (bottom of the fraction). Therefore, (x+2) can be omitted to simplify the algebraic fraction, just as removing and removing 5 from 15/35:
(x+2)(x-3) → (x-3)
(x+2)(x+10) → (x+10) So, the final answer is: (x-3)/(x+10)
Method 2 of 3: Simplifying Algebraic Fractions
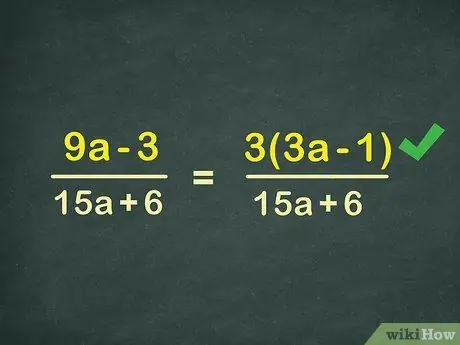
Step 1. Find the common factor of the numerator (top of the fraction)
The first step in simplifying an algebraic fraction is to simplify each part of the fraction. Do the numerator part first. Remove the common factors until you get the simplest expression. Example:
9x-3
15x+6
Do the numerator part: 9x - 3. The common factor of 9x and -3 is 3. Factor out the number 3 from 9x - 3 to make 3*(3x-1). Write the new numerator expression for the fraction:
3(3x-1)
15x+6
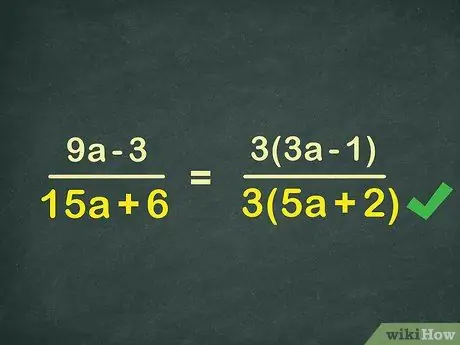
Step 2. Find the common factor in the denominator (bottom of the fraction)
Continuing to work on the example problem above, pay attention to the denominator, 15x+6. Again, find the number that divides the two parts of the expression. The common factor of 15x and 6 is 3. Factor 3 out of 15x+6 to make 3*(5x+2). Write the new denominator expression on the fraction:
3(3x-1)
3(5x+2)
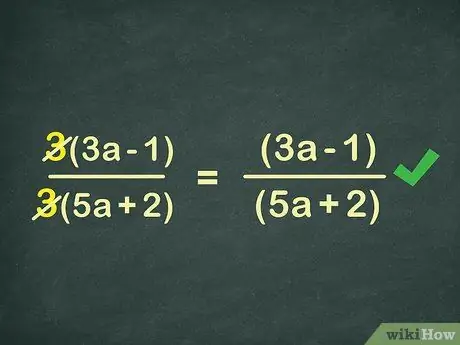
Step 3. Eliminate the same numbers
This step simplifies fractions. If the numerator and denominator have the same number, remove the number. In the example, the number 3 in the numerator and denominator can be omitted.
3(3x-1) → (3x-1)
3(5x+2) → (5x+2)
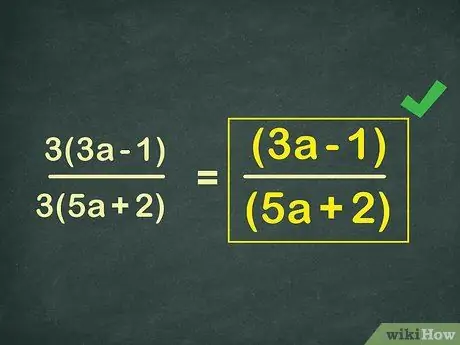
Step 4. Check if the algebraic fraction is at its simplest
The simplest algebraic fractions have no common factor in the numerator or denominator. Remember, factors in parentheses cannot be omitted. In the example problem, x cannot be factored out of 3x and 5x because the complete expressions are (3x-1) and (5x+2). So, the two expressions are already the simplest and obtained final answer:
(3x-1)
(5x+2)
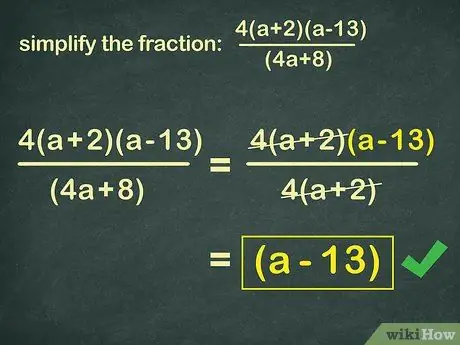
Step 5. Do the practice questions
The best way to master this topic is to keep practicing working on algebraic fraction simplification problems. Do the following two questions; The answer key is below the question.
4(x+2)(x-13)
(4x+8) Answer:
(x=13)
2x2-x
5x Answer:
(2x-1)/5
Method 3 of 3: Doing More Complicated Problems
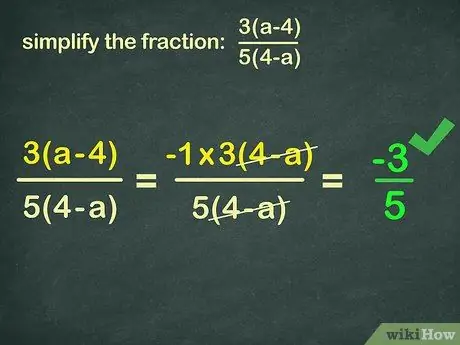
Step 1. “Invert” the fractional part by factoring out a negative number
Problems example:
3(x-4)
5(4-x)
(x-4) and (4-x) ''almost'' are the same. (x-4) and (4-x) cannot be eliminated because they are inverted. However (x-4) can be changed to -1*(4-x), just like changing (4 + 2x) to 2 * (2 + x). This method is called "factoring out negative numbers".
-1*3(4-x)
5(4-x)
Now both (4-x) can be omitted:
-1*3(4-x)
5(4-x)
So, the final answer is -3/5

Step 2. Identify the form of the difference of two squares when working on the problem
The difference between two squares is one squared minus the other (a.)2 - b2). The form of the difference of two squares is always simplified into two parts, adding and subtracting square roots:
a2 - b2 = (a+b)(a-b) This formula is very important for finding common factors in algebraic fractions.
Example: x2 - 25 = (x+5)(x-5)

Step 3. Simplify the polynomial expression
A polynomial is a complex algebraic expression that has more than two terms, for example x2 + 4x + 3. Fortunately, most forms of polynomials can be simplified by factorizing polynomials. Example: x2 + 4x + 3 can be simplified to (x+3)(x+1).
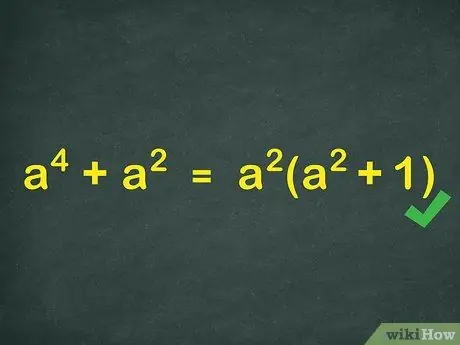
Step 4. Remember, variables can also be factored out
This is very important, especially in expressions that have exponents. Example: x4 +x2. Factor out the largest exponent. So, x4 +x2 = x2(x2 + 1).
Tips
- Always use the greatest common factor when simplifying to ensure that the final answer is in the simplest form.
- Check the answers by multiplying the common factors again. If your answer is correct, the multiplication returns the previous expression.






