- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
A rational equation is a fraction with one or more variables in the numerator or denominator. A rational equation is any fraction that involves at least one rational equation. Like ordinary algebraic equations, rational equations are solved by performing the same operation on both sides of the equation until the variables can be transferred to either side of the equation. Two special techniques, cross multiplication and finding the least common denominator, are very useful ways to move variables and solve rational equations.
Step
Method 1 of 2: Cross Multiplication
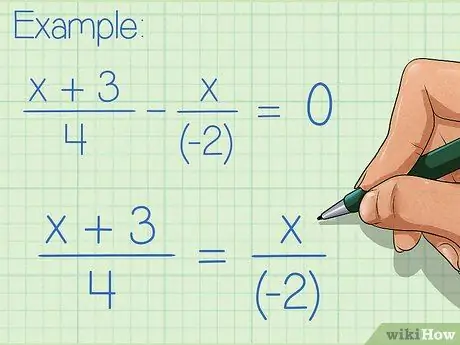
Step 1. If needed, rearrange your equation to get a fraction on one side of the equation
Cross multiplication is a quick and easy way to solve rational equations. Unfortunately, this method can only be used for rational equations that contain at least one rational equation or fraction on each side of the equation. If your equation doesn't meet these cross product requirements, you may have to use algebraic operations to move the parts to the right places.
-
For example, the equation (x + 3)/4 - x/(-2) = 0 can easily be put into cross product form by adding x/(-2) to both sides of the equation, so that it becomes (x + 3)/4 = x/(-2).
Note that decimal and whole numbers can be converted into fractions by giving the denominator 1. (x + 3)/4 - 2, 5 = 5, for example, can be rewritten as (x + 3)/4 = 7, 5/1, making it satisfy cross multiplication condition
- Some rational equations cannot easily be reduced to a form that has one fraction or rational equation on each side. In such cases, use the same least denominator approach.

Step 2. Cross multiply
Cross multiply means multiplying one of the numerators of a fraction by the denominator of another fraction and vice versa. Multiply the numerator of the fraction on the left by the denominator of the fraction on the right. Repeat with the right denominator with the left denominator.
Cross multiplication works according to basic algebraic principles. Rational equations and other fractions can be made into non-fractions by multiplying them by the denominator. Cross product is basically a quick way to multiply both sides of an equation by both denominators. Do not believe? Give it a try - you'll get the same result after simplifying it

Step 3. Make the two products equal to each other
After cross multiplying, you will get two multiplication results. Make them equal to each other and simplify to make the equation as simple as possible.
For example, if your original rational equation was (x+3)/4 = x/(-2), after cross multiplying, your new equation becomes -2(x+3) = 4x. If you want, you can also write it as -2x - 6 = 4x
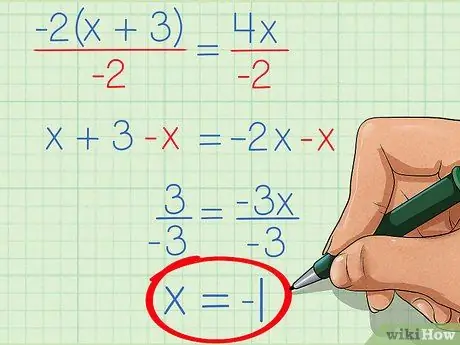
Step 4. Find the value of your variable
Use algebraic operations to find the value of your equation's variable. Remember that, if x appears on both sides of the equation, you must add or subtract x from both sides of the equation to leave x on only one side of the equation.
In our example, we can divide both sides of the equation by -2, so x+3 = -2x. Subtracting x from both sides gives 3 = -3x. Finally, by dividing both sides by -3, the result becomes -1 = x, which can be written as x = -1. We've found the value of x, solving our rational equation
Method 2 of 2: Finding the Least Common Denominator
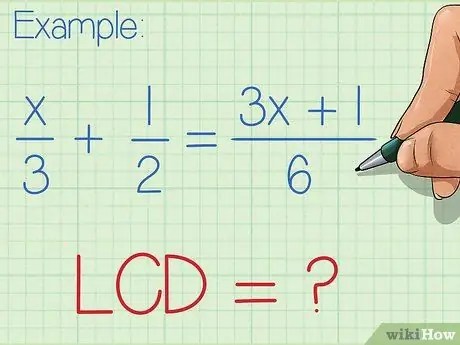
Step 1. Know the exact time to use the same smallest denominator
The same smallest denominator can be used to simplify rational equations, making them searchable for variable values. Finding the least common denominator is a good idea if your rational equation can't easily be written in terms of one fraction (and only one fraction) on each side of the equation. For solving rational equations with three or more parts, the least common denominator is helpful. However, to solve a rational equation with only two parts, it is faster to use cross product.
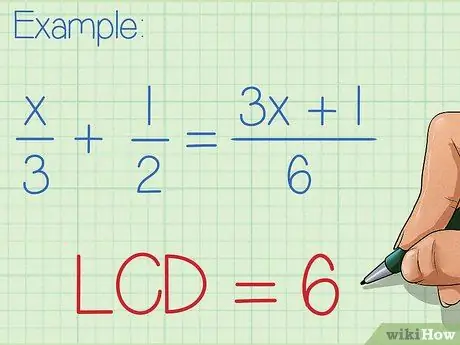
Step 2. Check the denominator of each fraction
Identify the smallest number that each denominator can divide and produce a whole number. This number is the least common denominator for your equation.
- Sometimes the smallest common denominator - that is, the smallest number that has all the factors in the denominator - is clearly visible. For example, if your equation is x/3 + 1/2 = (3x+1)/6, it's not hard to see the smallest number that has a factor of 3, 2, and 6, which is the number 6.
- However, often, the least common denominator of a rational equation is not clearly visible. In a case like this, try checking multiples of the larger denominator until you find a number that has a factor of all the other smaller denominators. Often, the least common denominator is the product of two denominators. For example, in the equation x/8 + 2/6 = (x-3)/9, the least common denominator is 8*9 = 72.
- If one or more of your fraction's denominators have variables, this process is more difficult, but possible to do. In a case like this, the least common denominator is an equation (with a variable) that is divisible by all the other denominators. For example in the equation 5/(x-1) = 1/x + 2/(3x), the least common denominator is 3x(x-1) because any denominator can divide it - dividing by (x-1) gives 3x, dividing by 3x gives (x-1), and dividing by x gives 3(x-1).
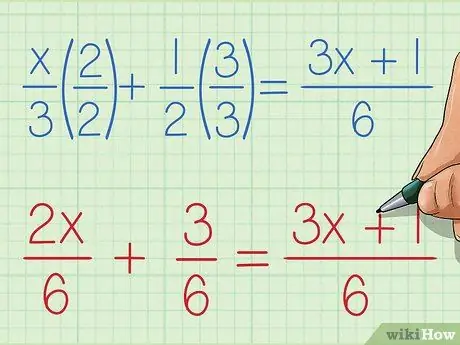
Step 3. Multiply each fraction in the rational equation by 1
Multiplying each part by 1 looks useless. But here's the trick. 1 can be defined as any number that is the same in both the numerator and denominator, such as -2/2 and 3/3, which is the correct way to write 1. This method takes advantage of the alternative definition. Multiply each fraction in your rational equation by 1, writing down the number 1 which when multiplied by the denominator gives the smallest common denominator.
- In our basic example, we'll multiply x/3 by 2/2 to get 2x/6 and multiply 1/2 by 3/3 to get 3/6. 2x + 1/6 already has the same smallest denominator, which is 6, so we can multiply it by 1/1 or leave it alone.
- In our example with a variable in the denominator of the fraction, the process is a little more complicated. Since our smallest denominator is 3x(x-1), we multiply each rational equation by something that returns 3x(x-1). We will multiply 5/(x-1) by (3x)/(3x) which gives 5(3x)/(3x)(x-1), multiply 1/x by 3(x-1)/3(x- 1) which results in 3(x-1)/3x(x-1), and multiplying 2/(3x) by (x-1)/(x-1) gives 2(x-1)/3x(x- 1).
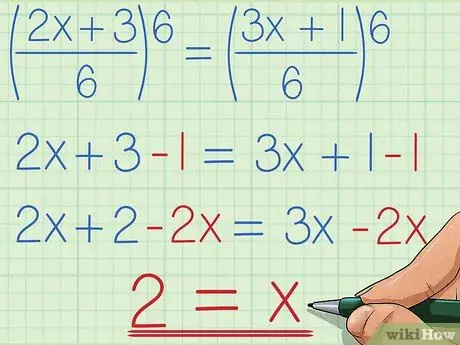
Step 4. Simplify and find the value of x
Now, since every part of your rational equation has the same denominator, you can remove the denominator from your equation and solve for the numerator. Multiply both sides of the equation to get the numerator value. Then, use algebraic operations to find the value of x (or whatever variable you want to solve) on one side of the equation.
- In our basic example, after multiplying all the parts by the alternative form 1, we get 2x/6 + 3/6 = (3x+1)/6. Two fractions can be added if they have the same denominator, so we can simplify this equation to (2x+3)/6 = (3x+1)/6 without changing the value. Multiply both sides by 6 to remove the denominator, so the result is 2x+3 = 3x+1. Subtract 1 from both sides to get 2x+2 = 3x, and subtract 2x from both sides to get 2 = x, which can be written as x = 2.
- In our example with a variable in the denominator, our equation after multiplying by 1 becomes 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1) /3x(x-1). Multiplying all the parts by the same smallest denominator, allowing us to omit the denominator, becomes 5(3x) = 3(x-1) + 2(x-1). This also applies to 5x = 3x - 3 + 2x -2, which simplifies to 15x = x - 5. Subtracting x from both sides gives 14x = -5, which, in the end, simplifies to x = -5/14.
Tips
- When you've solved the variable, check your answer by plugging the variable's value into the original equation. If your variable value is correct, you can simplify your original equation into a simple statement that always equals 1 = 1.
- Note that you can write any polynomial as a rational equation; put it above the denominator 1. So x+3 and (x+3)/1 have the same value, but the second equation can be classified as a rational equation because it is written as a fraction.






