- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Math is hard. It's easy to forget even the basic concepts when you try to remember the many different principles and methods. Here are two fresh ways to simplify fractions.
Step
Method 1 of 4: Using the Greatest Common Factor

Step 1. Write down the numerator and denominator factors
Factors are numbers that you can multiply to get another number. For example, 3 and 4 are factors of 12 because you can multiply them together to get 12. To write down the factors of a number, you just need to write down all the numbers that can be multiplied to get that number, and are divisible by the factors.
-
Write down the factors of the number from smallest to largest, without forgetting to include factor 1. For example, here's how you write down the numerator and denominator of the fraction 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Step 2. Find the greatest common factor (GCF) of the numerator and denominator
GCF is the largest number that can evenly divide two or more numbers. After you have written down all the factors of the number, all you have to do is find the largest number that is the same in both lists of factors.
-
24: 1, 2, 3, 4, 6,
Step 8., 12, 24.
-
32: 1, 2, 4,
Step 8., 16, 32.
-
The GCF of 24 and 32 is 8 because 8 is the largest number that can evenly divide 24 and 32.

Step 3. Divide the numerator and fraction by the GCF
Now that you've got the GCF, all you have to do is divide the numerator and denominator by that number to simplify your fraction to its simplest form. Here's how to do it:
- 24/8 = 3
- 32/8 = 4
- The simple fraction is 3/4.

Step 4. Check your work
If you want to make sure you've simplified the fraction correctly, you just need to multiply the new numerator and denominator by their GCF to get the original fraction back. Here's how to do it:
- 3 * 8 = 24
- 4 * 8 = 32
-
You have returned to its original form, which is 24/32.
You can also check the fraction to make sure it can't be simplified further. Since 3 is a prime number, it can only be divided by 1 and itself, and four is not divisible by 3, so the fraction cannot be simplified any further
Method 2 of 4: Keep Dividing by Small Numbers

Step 1. Choose a small number
Using this method, you only have to choose a small number, such as 2, 3, 4, 5 or 7, to start with. Look at the fractions to make sure that each part is divisible by the number you've chosen. For example, if you have the fraction 24/108, don't choose the number 5 because they are not divisible by 5. However, if you have the fraction 25/60, 5 is the right number to use.
For the fraction 24/32, 2 is a good number. Since both numbers are even numbers, they are divisible by 2

Step 2. Divide the numerator and denominator of the fraction by the number
The new fraction will consist of a new numerator and denominator, which you get after dividing the top and bottom of the fraction 24/32 by 2. Here's how to do it:
- 24/2 = 12
- 32/2 = 16
- Your new fraction is 12/16.
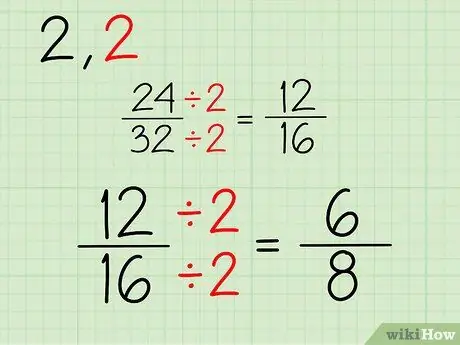
Step 3. Repeat
Continue this process. Since both numbers are even numbers, you can keep dividing by 2. If one or both of the numerators and denominators are odd numbers, then you can try dividing by another number. Here's the process for simplifying the 12/16 fraction:
- 12/2 = 6
- 16/2 = 8
- Your new fraction is 6/8.

Step 4. Keep dividing the number until it is no longer divisible
The new numerator and denominator are also even numbers, so you can keep dividing by 2. Here's how to do it:
- 6/2 = 3
- 8/2 = 4
- Your new fraction is 3/4.

Step 5. Make sure the fraction cannot be simplified any further
In the fraction 3/4, 3 is a prime number, so the factors are only 1 and itself, and 4 is not divisible by 3, so the fraction cannot be simplified any further. If the numerator or denominator of the fraction can no longer be divided by the number you selected, you may still be able to divide it by another number.
For example, if you have the fraction 10/40, and you divide the numerator and denominator by 5, the result is 2/8. You can't keep dividing the numerator and fraction by 5, but you can divide both by 2 so the end result is 1/4

Step 6. Check your work
Multiply 3/4 by 2/2 again three times, to make sure that you get the initial fraction, which is 24/32. Here's how to do it:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Notice that you are dividing 24/32 by 2 * 2 * 2, which is the same as dividing by 8, the largest GCF of 24 and 32.
Method 3 of 4: Writing the Factors

Step 1. Write down your fraction
Leave a large space on the right side of your paper - you will need it to write down the factors.

Step 2. Write down the factors of the numerator and denominator
Alone the factors of the two. The easiest way is for the factors to be written on top of each other. Start with the number 1 and write down the factors.
-
For example, if your fraction is 24/60, start with 24.
Write down: 24 -- 1, 2, 3, 4, 6, 8, 12, 24
-
Then, the number 60.
Write down: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Step 3. Find and divide by the greatest common factor
This term may be written as GCF in your printed book. What is the largest number that can divide the numerator and denominator? Whatever the number, divide both numbers by that number.
For our example, the largest number that is a factor of both numbers is 12. Thus, we divide 24 by 12 and 60 by 12, giving us 2/5 - our simple fraction
Method 4 of 4: Using a Prime Factor Tree

Step 1. Find the prime factors of the numerator and denominator
A prime number is a number that cannot be divided by any other number (other than itself and 1, of course). 2, 3, 5, 7, and 11 are examples of prime numbers.
- Start with the numerator. From 24, split into 2 and 12. Since 2 is already a prime number, you don't need to divide it anymore! Then break 12 into 2 numbers: 2 and 6. 2 are prime numbers - great! Now divide 6 into 2 numbers: 2 and 3. You now have 2, 2, 2 and 3 as your prime numbers.
- Now work on the denominator. From 60, split your tree into 2 and 30. 30 then divide into 2 and 15. Then divide 15 into 3 and 5, both of which are prime numbers. Now you have 2, 2, 3, and 5 as your prime numbers.
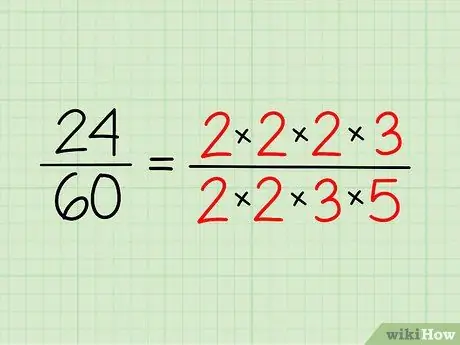
Step 2. Write down the prime factorization of each number
Write down the prime numbers you have for each number and write them in multiplication form. You don't have to multiply them - it's just a way to make them easier to see.
- So, for 24, you have 2 x 2 x 2 x 3 = 24.
- For 60, you have 2 x 2 x 3 x 5 = 60

Step 3. Eliminate the same factors
Any number that is part of both numbers can be discarded. In this example, the equal factors are a pair of 2s and one 3. Goodbye!
- The rest are 2 and 5 - or 2/5! The same answer we got the way above.
- If the fraction's numerator and denominator are even numbers, don't just divide by two. Continue to do the division until the number you get can not be divided again.






