- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
The mathematical concept of "probability" is related to, but different from, the concept of "probability". In simple terms, chance is a way of expressing the relationship between the number of desired outcomes in a given situation, versus the number of undesirable outcomes. Usually, this is expressed in a ratio (such as “1:3” or “1/3”). Calculating or calculating odds is central to strategy in many games of chance such as roulette, horse racing and poker. Whether you're a gambler or just plain curious, learning how to calculate odds can make playing games of chance even more fun (and profitable!).
Step
Part 1 of 3: Calculating Basic Odds
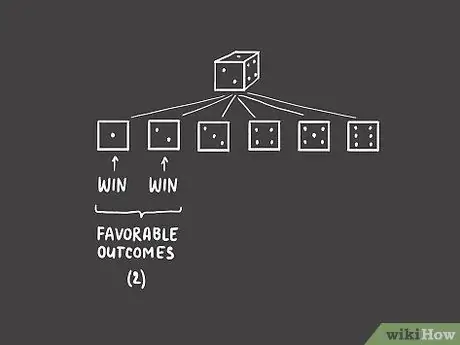
Step 1. Determine the number of desired outcomes in a situation
For example, we are planning to gamble but can only play one six-sided dice. In this case, we place a bet on what number the dice will appear after being thrown. Say, we bet on the number one or two. This means that there are two possibilities for us to win: if the dice shows a two, we win, and if the dice shows a 1. Thus, there are “two” desired outcomes.
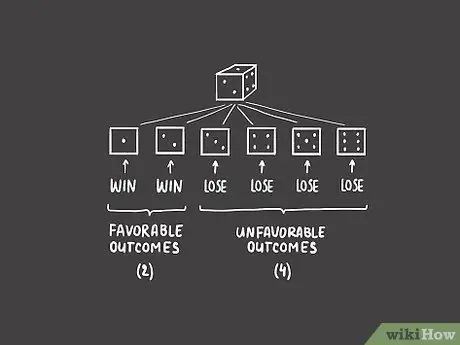
Step 2. Specify the desired number
In a game of chance, there is always a chance that you won't win. If we will get a number one or two, it means we will lose if what appears is a number three, four, five, or six. Since there are four possibilities for us to lose, it means that there are “four” undesirable outcomes.
- Another way to think of this is the “Total result number” minus the “desired number of results”. When rolling the dice, there are six possible totals-each representing a face and a number on the dice. So, in this example we can subtract two (desired numbers) from six probabilities: “6 - 2 = 4 unwanted outcomes”.
- As above, you can also subtract the number of unwanted results from the total number of results that appear, to find the number you want.
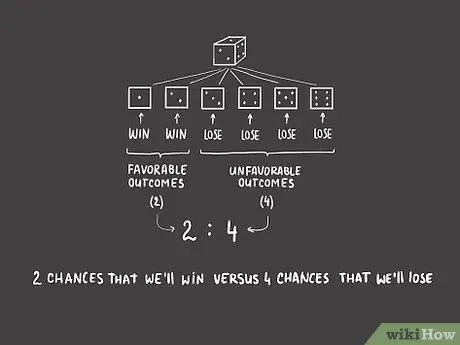
Step 3. Express the probability numerically
Usually, odds are expressed as the “ratio of desired to undesirable outcome”, and often a colon is used. In our example, the odds of success are: “2:4“, or two odds of winning against four odds of losing. As with fraction calculations, this can be simplified to: “1:2“by dividing both probabilities by the same multiplication factor, which is the number 2. This ratio is written (in a sentence) as "one-to-two odds".
You may present this ratio as a fractional calculation. If so, it means that our probability is "2/4", which is then simplified to "1/2". Please note that this “1/2” chance does not mean we have exactly half (50%) chance of winning. In fact, we have a one-third chance of winning. Keep in mind that when declaring these opportunities, there is likely to be a ratio of desired to undesired outcomes. "Not" is a numerical measurement of how much we have a chance of winning

Step 4. Know how to calculate the “opportunity as opposed to” the current event
The 1:2 odds we just calculated are our “support odds” of winning. What if we wanted to know the odds of losing, which are also known as “opportunities against” our winnings? To find this out, simply reverse the likelihood ratio to the desired number: “1:2” becomes “2:1”.
If you state the odds as opposed to winning in fractions, then you get "2/1". Remember, that as above, this is not an expression of how likely you are to lose, but should be read as a ratio of unwanted to desired results/numbers. If this is an understatement of how likely you are to lose, then you have a “200%” chance of losing, which is clearly impossible. How good? In fact, you have a “66%” chance of losing. That 2 possible loses and 1 possible win means 2 lose/3, then the total is = 0.66 = 66%

Step 5. Know the difference between chance and probability
The concepts of probability and probability are related, but not identical. Probability is a representation of the probability that a certain outcome will occur. It is expressed by dividing the desired number by the total number of possible outcomes. In our example, there is a "probability"' (not a chance) that we will get a one or two number (out of six possible outcomes of rolling the dice) is "2/6 = 1/3 = 0.33 = 33%". So, our 1:2 odds translate to a 33% chance that we will win.
- It's easy to switch between probability and chance. To find the likelihood ratio of a given probability, first express that probability as a division (we use “5/13”) here. Subtract the numerator (5) from the denominator (13) to "13 - 5 = 8". This answer is a number of unwanted results. Thus, the probability can be expressed as “5:8“, i.e. the ratio of the desired outcome to the undesirable.
- To find the probabilities of a given odds ratio, first express your odds as a division (we use “9/21”). Then add the numerator (9) and denominator (21) to "9 + 21 = 30". This answer is the total number of results. The probability can be expressed as “9/30 = 3/10 = 30%”-that is, the number of desired outcomes from the total number of possible outcomes.
- The simple formula for calculating the probability of a probability is “O = P/(1 - P)”. The formula for calculating the probability of an opportunity is "P = O/(O + 1)".
Part 2 of 3: Calculating Complex Odds
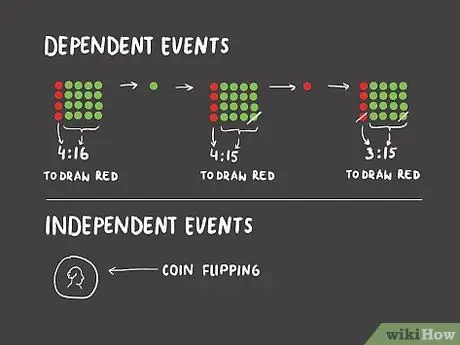
Step 1. Distinguish between dependent and independent events
In certain scenarios, the odds of a particular event will change based on the outcome of the past event. For example, if you have a jar of twenty marbles, four of which are red and the remaining sixteen are green, then you have a 4:16 (1:4) chance of getting a red marble at random. Say you draw a green marble. If you don't put the marble back in the jar, then on the next draw there will be a 4:15 chance of getting a red marble. Then, if you do get a red marble, you'll get a 3:15 (1:5) chance on the next draw. Drawing this red marble is referred to as a “dependent event”-that is, the probability that it “depends” on which marble has been drawn previously.
An “independent event” is an event whose probability is not affected by the previous event. Tossing a coin and getting a head side is called an independent event because you won't get that side based on whether the previous coin toss got heads or tails

Step 2. Determine if all results are evenly matched
If we roll a dice, then we can be sure that we will get the same chance for every number from 1 - 6. the chance. There is only one way to make a number 2, which is to roll two number 1 dice. Likewise, there is only one way to get a 12, which is to roll two dice with a number 6. On the other hand, there are many ways to get a number seven. For example, you can roll the dice with the numbers 1 and 6, 2 with 5, 3 with 4, and so on. In this case, the odds for each sum of the two dice should reflect the fact that some outcomes are easier to come up with than others.
- Let's try one example. To calculate the odds of rolling two dice totaling four (say 1 and 3), start by calculating the total that will come out. Each dice has six outcomes. Take the result number for each dice compared to the power of the dice number: “6(number of sides on each dice)2(number of dice) = 36 possible outcomes. “Next, find out how many ways you can make a four with two dice: You can roll the dice with a combination of 1 and 3, 2 with 2, or 3 with 1-there are three ways. So, the probability of getting a combination of dice with a result of "four" is "3:(36-3) = 3:33 = 1:11“
- Odds change “exponentially” based on the number of events occurring simultaneously. The chances of you getting "Yahtzee" (five dice with the same number) in one throw, are very slim: "6:65 - 6 = 6:7770 = 1:1295”!
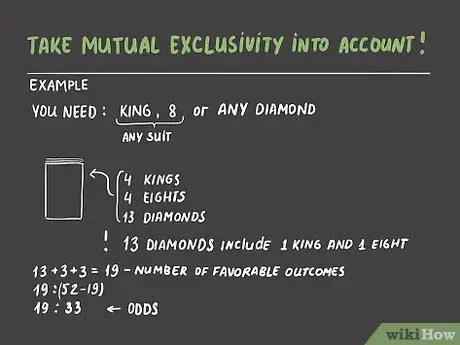
Step 3. Also calculate the exclusivity equation
Sometimes, multiple outcomes can overlap - the odds you take into account should reflect this. For example, if you play poker and get a nine, ten, prince and queen of diamonds, you'll want the next card to be a king or eight of either set (to get a straight), or, alternatively, any diamonds (to get a straight). got a flush). Let's say the dealer deals your next card from a standard deck of fifty-two cards. There are thirteen diamonds in the deck, containing four kings and four eights. However, the total number of desired outcomes is "not" 13 + 4 + 4 = 21. The thirteen diamonds already contain king cards and eight diamonds-we don't want to count twice. The actual sum of the desired results is "13 + 3 + 3 = 19". So, the odds of getting a card that will give you a straight or flush are "19:(52 - 19) or 19:33". Not bad!
In reality, of course, if you already have cards in your hand, there is very little chance of getting a card from a full deck of fifty-two cards, because the number of cards in the deck keeps decreasing as the cards are dealt. Also, if you are playing with other people, you have to guess, what cards they have when considering your own winning odds. This is the fun of playing poker
Part 3 of 3: Understanding the Odds in Gambling

Step 1. Know the general format for stating odds in gambling
If you are into the world of gambling, it is important to know that the number odds in betting do not reflect the real mathematical "odds" of a particular event. Instead, odds in the world of gambling, particularly in horse racing and sports betting, “reflect the amount the bookmaker will pay for the success of a bet”. For example, if you bet $100 on a horse with a 20:1 odds ratio against the horse, this does not mean that there are 20 outcomes where the horse loses and 1 result he wins. Instead, it means that you will have to pay “20 times” the value of your bet-in this case, $2,000! Even more confusing, the format of this opportunity statement sometimes varies, depending on the region. Here are some non-standard ways of expressing odds in gambling:
- “Decimal Probability (or "European Format"). “This is quite easy to understand. Decimal odds are expressed as a decimal number, such as 2.50”. This number is the payout ratio to the holder of the bet. For example, with a probability of 2.50, if you bet $100 and win, you will receive $250, or 2.5 times the original bet value. In this case, you make a profit of $150.
- “Fraction Chance (or “English Format”)”. Expressed as a fraction, such as “1/4”. It represents the ratio of the profit (not the total payout) of the successful bet to the holder of the bet. For example, if you bet $100 on something with a 1/4 Fraction Chance and it turns out to be a win, you will make a profit of 1/4 times the value of the original bet-in this case, your payout will be $125, for a profit of $25.
-
“Moneyline Opportunity (or USA Format). “This is a bit difficult to understand. Moneyline odds are expressed as a number preceded by a minus or plus sign, such as “-200” or “+50”. The minus sign means the number that represents how much you have to bet to get $100. A positive sign accompanies a number that represents how much you would win if you bet $100. Keep this subtle difference in mind! For example, if we bet $50 with Moneyline Odds of -200, then when we win we will get paid $75, for a total profit of $25. If we bet $50 with +200 Moneyline Odds, we will get paid $150 for a total profit of $100.
In Moneyline Odds, the number "100" (without a plus or minus sign) represents the value of a balanced bet - no matter how much money is wagered, you will still get that amount as profit if you win

Step 2. Understand how gambling odds are set
The odds set by bookies and casinos are usually not calculated based on the mathematical probability that a certain event will occur. They carefully determine that in the long run the bookie or casino will make money, no matter what the short term results are! Take this into account when placing your bets - and remember, that in the end, the bookie and casino “always” win.
Let's look at an example. A standard roulette wheel has 38 numbers-1 through 36, plus 0 and 00.. If you bet one number field in it (say “11”), you have a 1:37 chance of winning. However, the casino sets the payout odds at 35:1, meaning, if the ball lands on 11, you will win 35 times your bet. Note that the payout odds are slightly lower than your odds of losing. If the casino is not interested in making money, you should actually be paid at 37:1 odds ratio. However, by setting the payout odds slightly below your winning odds, the casino will earn money over time, even if it sometimes has to pay big payouts when the ball lands on 11

Step 3. Don't be fooled by gambling falsehoods
Gambling can be fun-even addictive. However, there are certain gambling strategies that are widely used and at first glance seem “natural”, but are actually, mathematically wrong. Here are a few things you should keep in mind when gambling: don't lose more money than you should!
- There is never a saying, "it's time to win" in gambling. If you play “Texas Hold 'Em” poker for an hour and still don't get a good hand, you're usually compelled to keep playing in the hope that a straight or flush is just a "wait of time". Unfortunately, your odds will never change no matter how long you spend gambling. Cards are always shuffled randomly before being dealt, so if you get ten bad cards in a row, you're more likely to keep getting cards like that, even a hundred times in a row. This also applies to all other games of chance such as roulette, slots, etc.
- Sticking with just one specific bet will not increase your odds. Maybe you know someone who has a "lucky" lottery number. While it's nice to be able to bet on numbers that have a special meaning personally, in a random game of chance, you can never win by betting on just one number at a time. But betting with different numbers is also the same. Lottery numbers, slots, and the roulette wheel are all deliberately random. In a game of roulette, for example, the odds are equal between you rolling the dice and getting a "9" three times in a row, with any three specific numbers in succession.
- If you feel "unbearable, one more point" from the number you want to win, believe that the number is never close. If you pick 41 while playing the lottery, while the winning number is 42, you may feel very sad, but be happy! In fact, that number will never be won. Two numbers that seem so close together, like 41 and 42, are mathematically completely unrelated in a random game of chance.
Tips
- Check the rules of the game for each specific game you play to get the information you need to calculate odds.
- Calculating lottery odds is much harder than one might think.
- Tables of odds that have been calculated for you, are available on the Internet.
- Look for websites with free odds counting services that will guide you through how the oddsmakers calculate the odds for a particular sporting event.






