A regular polygon is a convex 2-dimensional shape (having side angles less than 180 degrees) with congruent sides and equal angles. Many polygons, such as rectangles or triangles, have simple area formulas. However, if you're working with polygons that have more than 4 sides, the best way to solve this is to use a formula that uses the apothem and perimeter of the shape. With a little effort, you can find the area of a regular polygon in just a few minutes.
Step
Part 1 of 2: Calculating Area
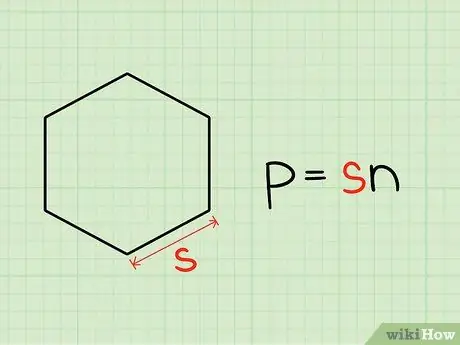
Step 1. Calculate the circumference
The perimeter is the combined length of the outlines of any two-dimensional shape. For regular polygons, the perimeter can be calculated by multiplying the length of one side by the number of sides (n).
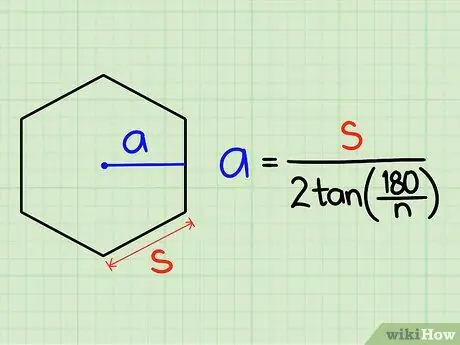
Step 2. Determine the apothem
The apothem of a regular polygon is the shortest distance from the center point to one of its sides by forming a right angle. Finding the apothem is a bit more complicated than calculating the perimeter.
The formula for calculating the length of the apothem is: the length of the side (s) divided by (2 times the tangent (tan) (180 degrees divided by the number of sides (n)))
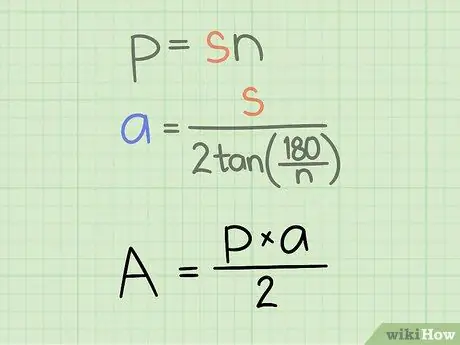
Step 3. Know the correct formula
The area of any regular polygon can be found using the formula: Area = (a x k)/2, with a is the length of the apothem and k is the perimeter of the polygon.
Step 4. Enter the values of a and k in the formula and find the area.
For example, let's use a hexagon (6 sides) with a side length (s) of 10.
- The perimeter is 6 x 10 (n x s) equals 60. So, k = 60.
- The apothem is calculated by a separate formula by entering 6 and 10 for the values of n and s. The result of 2 tons (180/6) is 1.1547. Then, 10 divided by 1.1547 equals 8.66.
- The area of the polygon is Area = a x k / 2 or 8.66 times 60 divided by 2. The area is 259.8 squared units.
- Also note that there are no parentheses in the area equation so if you calculate 8.66 divided by 2 times 60, the result will be the same as 60 divided by 2 times 8.66.
Part 2 of 2: Understanding Concepts in a Different Way
Step 1. Understand that a regular polygon can be thought of as a collection of triangles
Each side represents one base of the triangle and the number of triangles in the polygon is equal to the number of sides. Each triangle has the same base length, height and area.
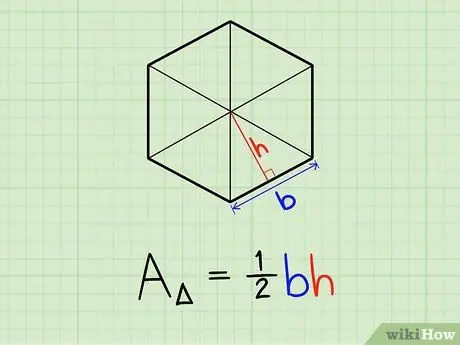
Step 2. Remember the formula for the area of a triangle
The area of any triangle is 1/2 times the length of the base (the length of the inner side of the polygon) times the height (the apothem of a regular polygon).
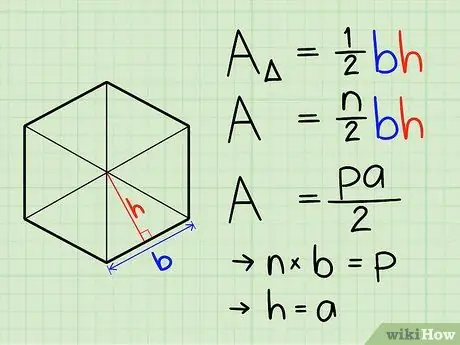
Step 3. Look at the similarities
Again, the formula for a regular polygon is 1/2 times the apothem times the circumference. The perimeter is simply the length of one side times the number of sides (n). For regular polygons, n also represents the number of triangles that make up the figure. Thus, the formula is simply the area of the triangle times the number of triangles in the polygon.
Tips
- For more information on how to do square roots, read the articles on How to Multiply Square Roots and How to Divide Square Roots.
- If your octagon (or other polygon) is already divided into its constituent triangles and you know the area of one of the triangles in the problem, you don't need to know the apothem. Just use the area of one triangle and multiply by the number of sides of the original polygon.
