- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
To add or subtract fractions with different denominators (the number at the bottom), you must first find the smallest common denominator of all the fractions. This value is the smallest multiple of all the denominators, or the smallest integer that can be divided by each denominator. You may also come across the term least common multiple. Although the term generally refers to integers, the way to find them is basically the same. Determining the least common denominator allows you to convert all the denominators in the fraction to the same number so that they can be added or subtracted by each other.
Step
Method 1 of 4: Compiling a List of Multiples
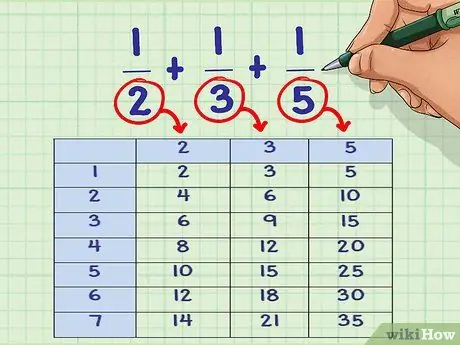
Step 1. List the multiples of each denominator
List the multiples of each denominator in the problem. Each list must consist of multiplying the denominator by the numbers 1, 2, 3, 4, and so on.
- Example: 1/2 + 1/3 + 1/5
- Multiples of the number 2: 2 * 1 = 2; 2 * 2 = 4; 2 * 3 = 6; 2 * 4 = 8; 2 * 5 = 10; 2 * 6 = 12; 2 * 7 = 14; etc.
- Multiple of 3: 3 * 1 = 3; 3 * 2 = 6; 3 *3 = 9; 3 * 4 = 12; 3 * 5 = 15; 3 * 6 = 18; 3 * 7 = 21; etc.
- Multiples of the number 5: 5 * 1 = 5; 5 * 2 = 10; 5 * 3 = 15; 5 * 4 = 20; 5 * 5 = 25; 5 * 6 = 30; 5 * 7 = 35; etc.
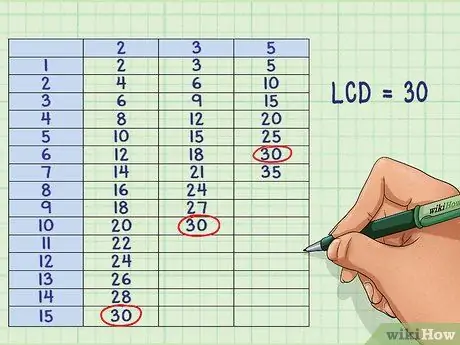
Step 2. Find the least multiple of the same number
Look at each list of multiples of denominators and mark all the numbers that belong to all three. After finding common denominators, determine the smallest common denominator.
- Note that if there are no common multiples in the list, you'll need to keep writing multiples of the denominator until you get the same number.
- This method is easier to use if the number in the denominator is small.
-
In the example above, all three denominators have the same multiple, which is 30: 2 * 15 =
Step 30.; 3 * 10
Step 30.; 5 * 6
Step 30.
- So, the least common denominator = 30
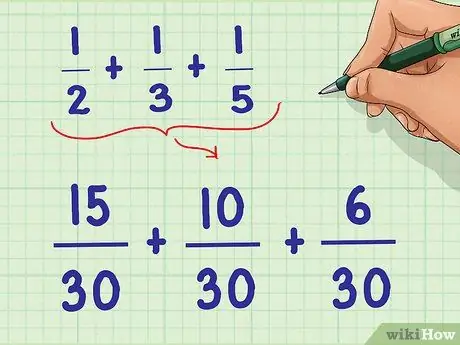
Step 3. Write down the question again
To convert all fractions into new fractions with equivalent values, you must multiply each numerator (the number at the top of the fraction) and denominator by the same factor to get the same smallest denominator.
- Example: (15/15) * (1/2); (10/10) * (1/3); (6/6) * (1/5)
- The new equation: 15/30 + 10/30 + 6/30
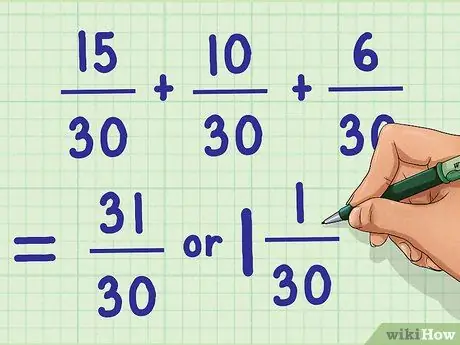
Step 4. Complete the rewritten problem
Once you've found the least common denominator and changed the fractions accordingly, you should be able to solve the problem easily. Remember to simplify your final calculation again.
Example: 15/30 + 10/30 + 6/30 = 31/30 = 1 1/30
Method 2 of 4: Using the Greatest Common Factor
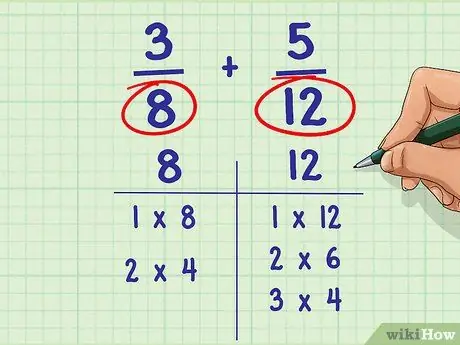
Step 1. List all the factors of each denominator
A factor is a number that is evenly divisible by an integer. The number 6 has four factors, namely: 6, 3, 2, and 1. All numbers have 1 as a factor because all numbers can be multiplied by 1.
- For example: 3/8 + 5/12.
- Factors of the numbers 8: 1, 2, 4, and 8
- Factors of the numbers 12: 1, 2, 3, 4, 6, 12
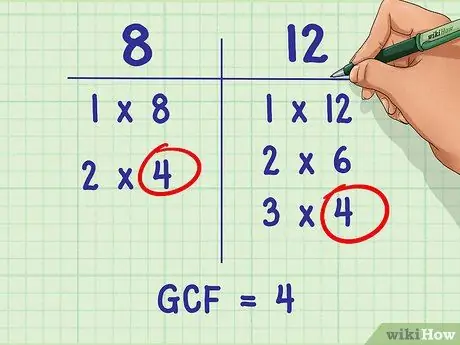
Step 2. Determine the greatest common factor between the two denominators
After listing the factors of each denominator, circle all the values that are the same in both. The greatest factor value is the greatest common factor (GCF) that will be used to solve the problem.
- In the example here, 8 and 12 have the same three factors: 1, 2, and 4.
- The greatest common factor is 4.
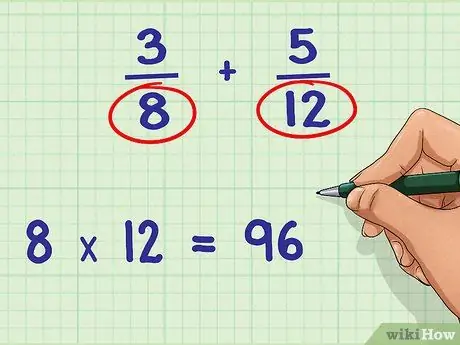
Step 3. Multiply all the denominators
Before using the greatest common factor to solve the problem, you must first multiply the two denominators.
Continuing the problem: 8 * 12 = 96
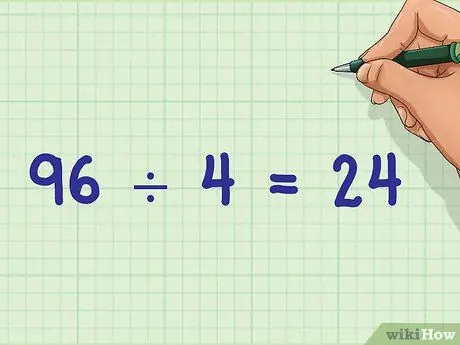
Step 4. Divide the product of the denominator by the GCF
Once you've found the product of the denominators, divide that number by the GCF you know beforehand. The result of the division is the smallest common denominator.
Example: 96 / 4 = 24
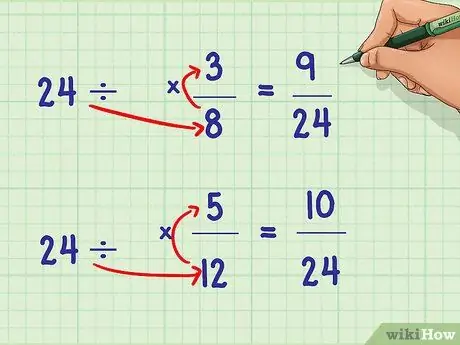
Step 5. Divide the smallest denominator that is the same as the original denominator in the problem
To find a multiplier that equals fractions, divide the smallest denominator that is the same as the original denominator. Multiply the numerator and denominator of both fractions by that number. Both denominators should now be equal to the value of the smallest common denominator.
- Example: 24 / 8 = 3; 24 / 12 = 2
- (3/3) * (3/8) = 9/24; (2/2) * (5/12) = 10/24
- 9/24 + 10/24
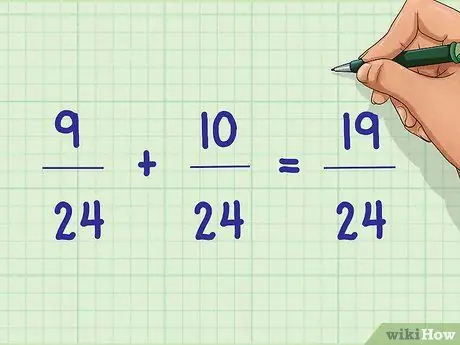
Step 6. Complete the rewritten problem
Once you've found the least common denominator, you should be able to add and subtract fractions in problems with ease. Remember to simplify the final calculation if possible.
Example: 9/24 + 10/24 = 19/24
Method 3 of 4: Factoring All Denominators to Primes

Step 1. Factor the denominator into a prime number
Factor all the denominators into prime numbers which, when multiplied, give that value. A prime number is a number that cannot be divided by any other number.
- Example: 1/4 + 1/5 + 1/12
- Prime factorization of the number 4: 2 * 2
- Prime factorization of the number 5:5
- Prime factorization of the number 12: 2 * 2 * 3
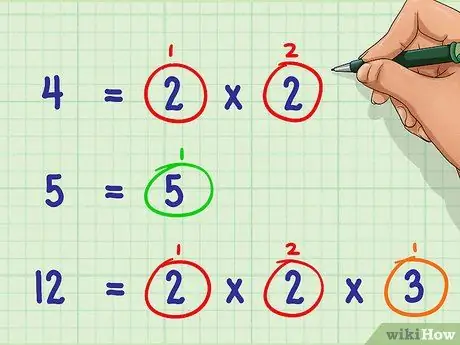
Step 2. Count the number of occurrences of each prime number in the factorization
Add up the occurrences of each prime number in the factorization of each denominator.
-
Example: there are two numbers
Step 2. in the factorization of the number 4; no numbers
Step 2. in the factorization of the number 5; and two numbers
Step 2. in the factorization of the number 12
-
No numbers
Step 3. in the factorization of numbers 4 and 5; and one number
Step 3. in the factorization of the number 12
-
No numbers
Step 5. in the factorization of numbers 4 and 12; one number
Step 5. in the factorization of the number 5
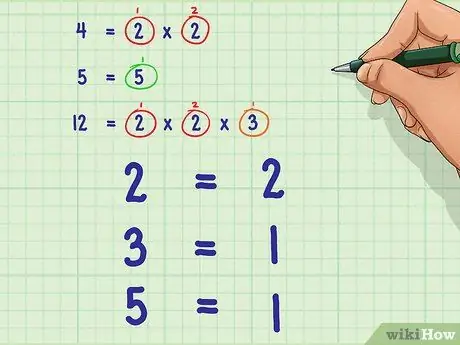
Step 3. Use the prime number that occurs the most
Find the prime number that occurs the most in the factorization of each denominator, and record the number of occurrences.
-
For example: Most occurrences of numbers
Step 2. is two, the most occurrences of numbers
Step 3. is one, and the most occurrences of numbers
Step 5. is one.
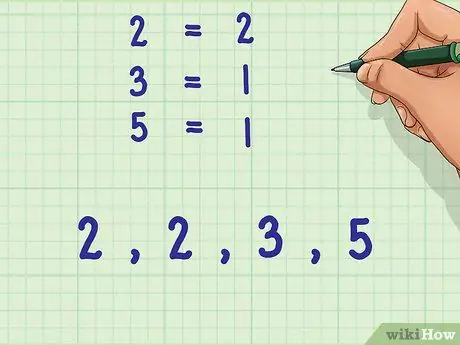
Step 4. Write down as many prime numbers as they occur
Do not list the number of occurrences of prime numbers in the factorization of the denominator. Simply write down the prime number that occurs the most, as determined in the previous step.
Example: 2, 2, 3, 5

Step 5. Multiply all prime numbers written in this way
Multiply the prime numbers as listed in the previous step. The product of this product is the same as the smallest common denominator in the original problem.
- Example: 2*2*3*5 = 60
- The least common denominator = 60

Step 6. Divide the smallest denominator that is the same as the original denominator
To determine the number of multipliers needed to balance fractions, divide the smallest denominator that is the same as the original denominator. Multiply the numerator and denominator of each fraction by the result of the division. The denominator should now be the same as the smallest common denominator.
- Example: 60/4 = 15; 60/5 = 12; 60/12 = 5
- 15 * (1/4) = 15/60; 12 * (1/5) = 12/60; 5 * (1/12) = 5/60
- 15/60 + 12/60 + 5/60
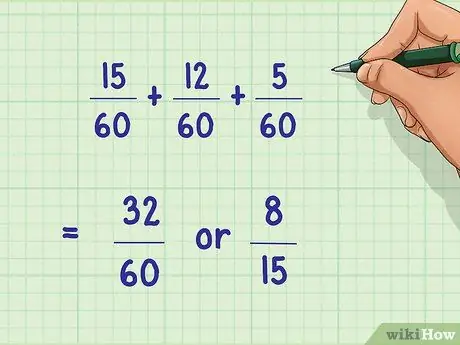
Step 7. Complete the rewritten problem
Once you've found the least common denominator, you should be able to add and subtract fractions as you normally would. Remember to simplify the fraction at the end of the calculation if possible.
Example: 15/60 + 12/60 + 5/60 = 32/60 = 8/15
Method 4 of 4: Doing Integer and Mixed Number Problems

Step 1. Convert all integers and mixed numbers into improper fractions
Convert mixed numbers to improper fractions by multiplying the number by the denominator and adding the numerator to the result. Convert an integer to an improper fraction by putting 1 as the denominator.
- Example: 8 + 2 1/4 + 2/3
- 8 = 8/1
- 2 1/4; 2 * 4 + 1 = 8 + 1 = 9; 9/4
- Rewrite the question: 8/1 + 9/4 + 2/3
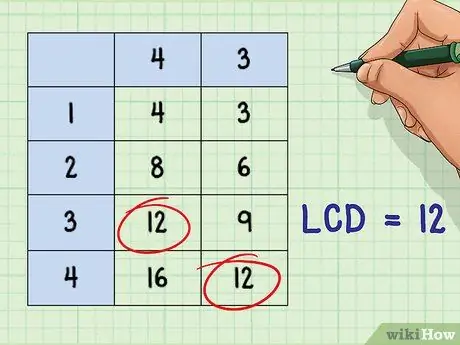
Step 2. Find the smallest common denominator
Use one of the ways to find the least common denominator in common fractions as described above. Notice in the example here we will use the "list of multiples" method, which is to create a list of multiples of each denominator and find the smallest common denominator from the list.
-
You don't need to list multiples of numbers
Step 1. because all numbers are multiplied
Step 1. equal to the number itself; in other words, all numbers are multiples of number
Step 1..
-
Example: 4 * 1 = 4; 4 * 2 = 8; 4 * 3 =
Step 12.; 4 * 4 = 16; etc.
-
3 * 1 = 3; 3 * 2 = 6; 3 * 3 = 9; 3 * 4 =
Step 12.; etc.
-
The least common denominator =
Step 12.
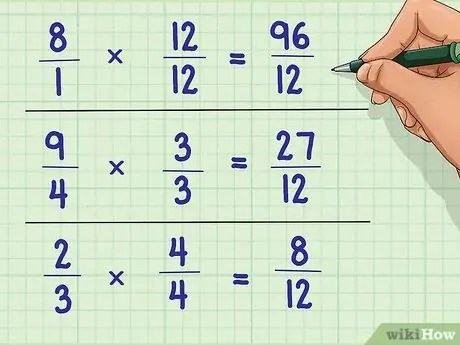
Step 3. Rewrite the original problem
Instead of just multiplying the denominators, you have to multiply the entire fraction by the number needed to turn the denominators into the same smallest denominator.
- Example: (12/12) * (8/1) = 96/12; (3/3) * (9/4) = 27/12; (4/4) * (2/3) = 8/12
- 96/12 + 27/12 + 8/12
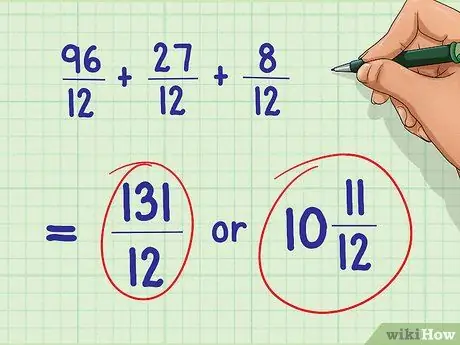
Step 4. Solve the problem
Once you've found the least common denominator and balanced the fractions according to that value, you should be able to add and subtract fractions easily. Remember to simplify the final calculation result if possible.






