- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Place value, or the concept that the value of a number (0-9) is determined by its position in a particular number, is a fundamental concept in mathematics. Since this concept is so easy for people who already understand it, teaching it can be quite complicated. However, once students grasp this concept, they will be ready and excited to use their new skills and learn more complex mathematical concepts.
Step
Part 1 of 3: Introducing the Basic Concepts

Step 1. Take the time to teach place value
If you teach within a predefined curriculum scope, you should already have an idea of how to adapt place value to a wider range of learning. If you tutor or teach at home, the learning structure will be more flexible. Plan to teach place value sometime after students have finished learning to count and performing simple addition and subtraction operations - usually around grade 1 or grade 2. An understanding of place value will provide a basis for these children to understand more complex mathematical concepts.

Step 2. Introduce the concept of counting groups of numbers
Most of the children's students only learn to count numbers one by one: one… two… three… four. This is sufficient for basic addition and subtraction, but still too simple to provide a solid basis for understanding more complex functions. Before you teach them how to break down large numbers into their respective place values, it's a good idea to teach them to break a group of small numbers into large numbers.
- Teach your students how to count two two, three three, five five, and ten ten. This is a fundamental concept for students to understand before they learn about place value.
- In particular, try to build a strong "thrill of tens". Modern mathematics uses the number ten as a base, making it easier for children to learn more complex systems if they get used to thinking this way. Teach your students to instinctively group numbers into sets of ten.

Step 3. Review the concept of place value
Refresh your understanding. Make sure you fully understand this concept yourself before trying to teach it to a group of young students. Simply put, place value is the idea that the value of a number (0-9) depends on its "place" or position in a number.

Step 4. Explain the difference between numbers and numbers
Numbers are symbols of the ten basic numbers that make up all numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. These numbers are combined to form all other numbers. A number can be a number (eg the number 7), but only if it is not grouped with other numbers. When two or more numbers are grouped together, the sequence of the numbers forms the larger number.
Show that by itself "1" is the number one and "7" is the number seven. When grouped as "17", the two numbers form the number seventeen. Similarly, "3" and "5" together form the number thirty-five. Show some other examples so students can go home understanding
Part 2 of 3: Teaching by Visual Examples
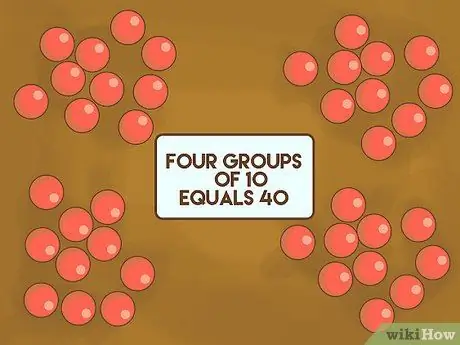
Step 1. Show the children that counting ten to ten is easier
Use 30 - 40 objects that are small, countable, and fairly homogeneous. For example: pebbles, marbles, or an eraser. Spread it out on the table in front of the students. Explain that in modern mathematics, we use the number 10 as a basis. Arrange the objects into several groups, then count them in front of the class. Show them that four groups of 10 pebbles equal 40.

Step 2. Translate the example with pebbles into written numbers
Write the concept sketch on the blackboard. First, create a regular T-chart. Write the number 1 in the upper right corner of the T chart. Then, write the number 10 in the upper left. Write a 0 in the column on the right labeled "1", and write a 4 in the column on the left labeled "10". Now you can explain to the class that each number made with pebbles has its own "place".
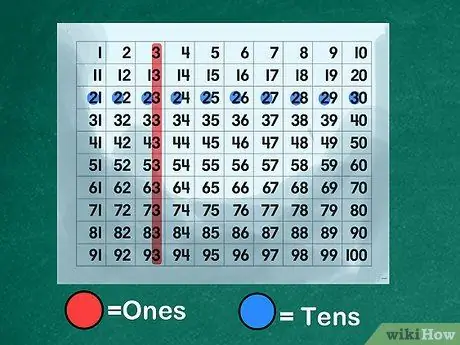
Step 3. Use a number pad to illustrate the place value basis
Create or print a "number pad" that displays all the numbers in order from 1 to 100. Show students how the numbers 0 to 9 interact with the numbers 10 to 100. Explain that each number from 10 to 99 is made up of two digits, one a number in the "ones" place and another number in the "tens" place. Show that the number "4" represents "four" when in the "ones" place, but serves as a prefix for the number "40" when it is in the "tens" place.
- Illustrate the place of "units". Direct the class to name all the numbers that have the digit "3" in the "ones" place: 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Explain about the "tens" place. Instruct students to designate all numbers that have a "2" in place of "tens": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Explain that the "3" in "23" is stacked on top of " 20" marked with the number "2." Teach your kids to read the place "tens" as a trigger for learning.

Step 4. Experiment with other visual teaching tools
You can arrange physical objects or draw them on the board. You can explain place value by using increments of monetary value, which students may have already studied, to relate them to scaled numerical values. For a fun and interactive activity, try using the students themselves as "group" grades.
Human memory is dominated by visual things, so the concept of place value is still abstract until you can make it visual. Meanwhile, numeric symbols themselves can still be abstract for children! Look for ways to frame group counting and place value activities so that they are simple, tangible, and intuitive
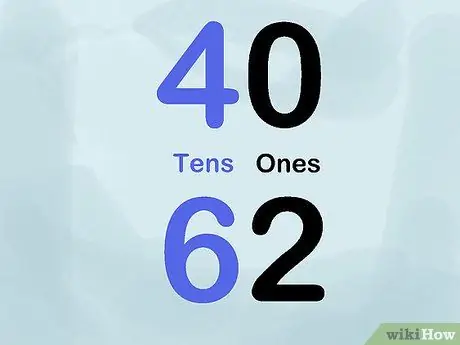
Step 5. Use color
Try using different colored chalk or markers to demonstrate place value. For example, write various numbers with a black marker for the "ones" place and a blue marker for the "tens" place. Thus, you would write 40 with the number "4" in blue and the number "0" in black. Repeat this trick for a large number of numbers to show the application of place value on the board.
Part 3 of 3: Use Interactive Examples
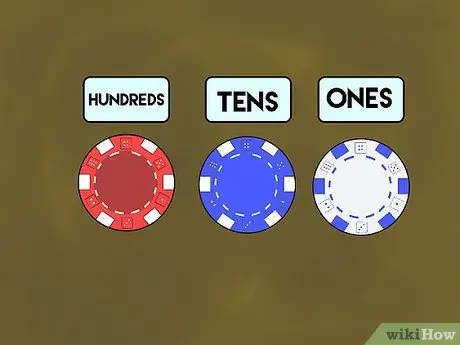
Step 1. Teach with poker chips
First, distribute the poker chips to each student. Tell them that the white chips represent the "ones" place, the blue chips for "tens", and the red chips represent the "hundreds". Next, show your students how to make numbers using place values in the form of colorful chips. Name a number (say 7) and place the white chip to the right of your desk.
- Name another number - for example, 30. Put three blue chips that represent 3 (in the "tens" place) and zero white chips to represent 0 (in the "ones" place).
- You don't have to use poker chips. You can use any object to represent the three basic "place" values as long as each group (chip color, etc.) is standard, homogeneous, and easily recognizable.

Step 2. Instruct students to exchange pieces with each other
This method can illustrate the low place values that make up the higher place values. Once students have demonstrated a good understanding of place value, teach your class how to swap white "ones" chips for blue "tens" chips, then trade "tens" chips for "hundreds." Ask students, "How many blue chips do I get by exchanging 16 white chips? If I exchange three blue chips, how many white chips do I get?"

Step 3. Show how to do addition and subtraction with poker chips
This concept can only be taught after students have mastered the exchange of poker chips. It is helpful to start by writing an example.
- For the basic addition problem, direct students to lay down three blue chips (tens) and six white chips (ones). Ask students about the numbers formed with the chips. (The answer is 36!)
- Keep working on the same number. Have your students add five white chips to the number 36. Ask them about the current number. (The answer is 41!) Next, take a blue chip and ask them the current number. (The answer is 31!)






