- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
The formula for calculating the circumference (“K”) of a circle, “K = D” or “K = 2πr” is easy to use if you know the diameter (“D”) or the radius (“r”). But what if you only knew the breadth? As with any math problem, there are several answers to this problem. The formula “K = 2√πL” is designed to find the circumference of a circle based on its area (“L”). Alternatively, you can solve the equation “L = r2” in reverse to find the length of the radius of the circle, then enter the length of the radius into the formula for the circumference of a circle. Both formulas or equations give the same result.
Step
Method 1 of 2: Using the Perimeter Equation

Step 1. Use the formula “K = 2√πL” to solve the problem
This formula works to measure the circumference of a circle if you only know its area. "K" stands for circumference, and "L" stands for area of a circle. Write and use this formula to start solving the problem.
- The symbol “π” (represents pi) is a repeating decimal number that has thousands of decimal places. For simplicity, use the constant 3, 14 to represent pi.
- Since you need to convert pi to its numeric form, plug 3, 14 into the formula from the start. Therefore, you can write this formula as “K = 2 3, 14 x L”.
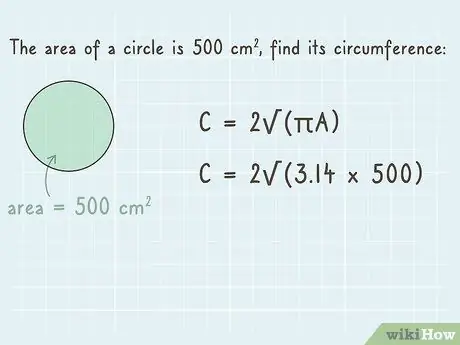
Step 2. Enter the area of the circle to the “L” position in the formula
Since you already know the area of the circle, enter the value in the “L” position. After that, solve the problem using the order of operations.
Let's say the area of the existing circle is 500 cm2. You can write the equation as “2 3, 14 x 500”.

Step 3. Multiply pi by the area of the circle
In a sequence of mathematical operations, the operations inside the root symbol need to be calculated first. Multiply pi by the area of the circle you entered. After that, add the result into the equation.
If you have the problem “2 3, 14 x 500”, multiply 3, 14 by 500 to get 1,570. Now, the equation will look like this: “2 1.570”
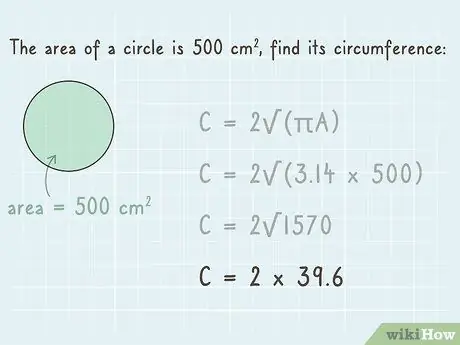
Step 4. Find the square root of the product
There are several ways to calculate the square root of a number. If you are using a calculator, press the “√” key and type in a number. You can also calculate the square root manually using prime factorization.
The square root of 1570 is 39, 6
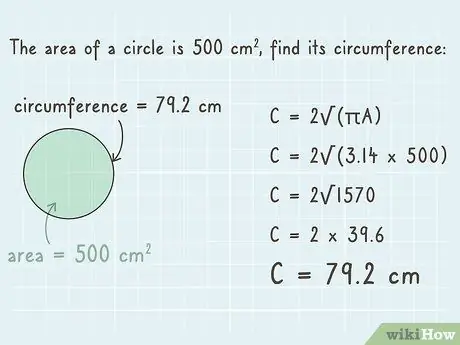
Step 5. Multiply the square root of the product by 2 to find the circumference of the circle
Finally, multiply the square root result by 2 to complete the formula. You will get the final result which is the circumference of the circle.
Multiply 39.6 by 2 to get 79.2. This means that the circumference of the circle is 79.2 cm and the equation has been successfully solved
Method 2 of 2: Solving Problems Reverse

Step 1. Use the formula “L = r2”.
This formula is used to find the area of a circle. “L” represents the area of the circle, while “r” represents the radius. Usually, you will use this formula if you already know the radius of the circle. However, you can also enter the area of a circle to reverse the equation and find the length of the circle's radius.
Again, use the constant 3, 14 to represent pi
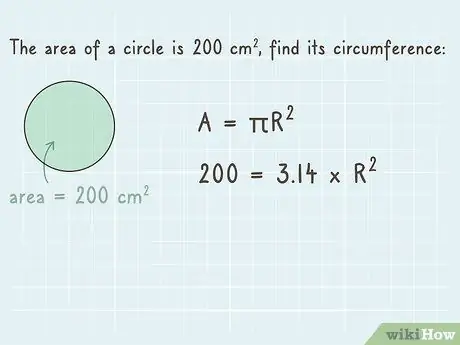
Step 2. Enter the area to the “L” position in the formula
Use any number to represent the area of a circle. Enter the number on the left side of the equation in the "L" position.
Let's say the area of the existing circle is 200 cm2. The formula you use is “200 = 3.14 x r2”.
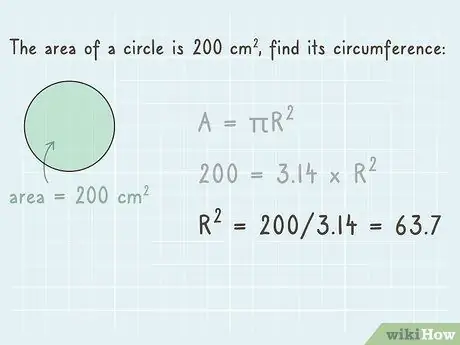
Step 3. Divide the number on both sides by 3, 14
To solve an equation like this, gradually eliminate the step on the right side by performing the inverse operation. Since you already know the value of pi, divide each side by that value. This way, you can omit pi on the right side of the equation, and you'll get a new number on the left.
If you divide 200 by 3, 14, you get 63, 7. Now you have a new equation, which is “63, 7 = r2”.
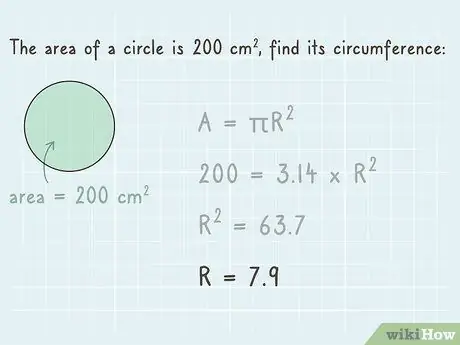
Step 4. Find the square root of the division to find the length of the circle's radius
In the next step, remove the exponent on the right side of the equation. The opposite of the square root is the square root. Find the square root of the number on each side of the equation. Thus, the exponent on the right side of the equation can be removed and you can get the length of the radius of the circle on the left side of the equation.
The square root of 63, 7 is 7, 9. Therefore, the equation will be “7, 9 = r” which indicates that the length of the radius of the circle is 7, 9. This mathematical operation already provides all the information you need to know circumference

Step 5. Find the circumference of the circle using its radius
There are two formulas that can be used to calculate the circumference ( K). The first formula is “K = D”, where “D” is the diameter of the circle. Multiply the radius by two to find the diameter of the circle. The second formula is “K = 2πr”. Multiply 3, 14 by 2, then multiply the result by the length of the radius. Both formulas will give the same result.
- In the first formula, 7, 9 x 2 = 15, 8 (diameter of the circle). Multiply the diameter by 3.14 to get 49.6 (the circumference of the circle).
- In the second formula, write the equation as 2 x 3, 14 x 7, 9. First, 2 x 3, 14 = 6, 28. Multiply the product by 7, 9 to get 49, 6. Now, notice that both formulas give same answer.






