- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Converting numbers between percents, fractions (fractions), and decimals is an important math skill. After learning it you will know that the concept is very simple. You will not only know how to convert small numbers that will help you with your exams, but will also be useful for doing financial/financial calculations.
Step
Method 1 of 3: Changing Percent

Step 1. To convert a percent to a decimal, move the decimal sign two places to the left
Unless otherwise noted, in percent, the decimal point is at the end of the last number. For example, imagine that 75% actually appears as 75.0%. Moving the decimal sign two places to the left converts the percent to a decimal. This method is the same as dividing a number by 100. Example:
- 75% changed to 0.75
- 3.1% changed to 0.031
- 0.5% changed to 0.005

Step 2. Display the percent as a fraction of 100
Writing a number as a fraction of 100 is another simple way to write a percent. The number of percent is the numerator of the fraction, while 100 is the denominator. Simplify the fraction to its smallest form.
- Example: 36% turns into 36/100.
- For simplicity's sake, find the highest number that goes into 36 and 100. In this case, that number is 4.
- Determine how many times 4 goes into 36 and 100. When you simplify, the answer is 9/25.
- To check that you made the conversion correctly, divide 9 by 35 (0, 36) and multiply by 100 (36%). This number must be the same as the original percentage.

Step 3. Remove the percent sign
As soon as a percent is converted to a decimal or fraction, the use of the % sign is no longer appropriate. Keep in mind that percent means “hundredths”, so if you forget to remove the percent sign after converting it (to a decimal or fraction), your answer will no longer correspond to a hundred.
Method 2 of 3: Converting to Decimal

Step 1. Multiply the decimal by 100 to convert it to a percent
In other words, move the decimal point two places to the right. Percent means “hundredths”, so the decimal will become “hundredths” once multiplied. Don't forget to add the percent sign/symbol (%) after multiplication. For example: 0.32 becomes 32%, 0.07 becomes 7%, 1.25 becomes 125%, 0.083 becomes 8.3%.

Step 2. Convert the ending decimal to a fraction
An ending decimal is a non-repeating decimal number. Move the decimal point to the right as many decimal places as there are. The number is now the numerator of the fraction. While the denominator is 1 with as many zeros as the decimals in the original number. As a final step, simplify the fraction.
- For example: 0, 32 has two decimal places. Move the decimal point two places to the right and divide by 100, the result is: 32/100. With 4 as a common factor (number and denominator), the fraction can be simplified to 8/25.
- Another example: 0, 8 has only one decimal place. Move the decimal point one place to the right and divide by 10, the result: 8/10. With 2 as a common factor, the fraction can be simplified to 4/5.
- To check, you can simply divide the resulting fraction, and make sure that the number is the same as the original decimal: 8/25 = 0.32.

Step 3. Convert repeating decimals to fractions
A repeating decimal is a decimal number that has a series of numbers that repeats continuously. For example, if the repeating decimal number is 0, 131313… in that number there are 2 repeating decimals (13 is repeating). Determine how many repeating decimals there are then multiply the decimal by 10 , where n is the number of repeating decimals.
- For example, 0, 131313… multiplied by 100 (10 to the power of 2) and we get 13, 131313…
- To determine the numerator (the number at the top), subtract the repeating part from the decimal. For example, 13, 131313… - 0, 131313… = 13, so the numerator is 13.
- To determine the denominator (the number below), subtract 1 from the number you used to multiply. For example, 0, 131313… is multiplied by 100, so the denominator is 100 - 1 = 99.
- The final fraction for 0, 131313… is 13/99
-
Some additional examples:
- 0, 333… becomes 3/9
- 0, 123123123… becomes 123/999
- 0, 142857142857… becomes 142857/999999
- If necessary, convert the fraction to its smallest form. For example, 142857/999999 becomes 1/7.
Method 3 of 3: Converting Fractions
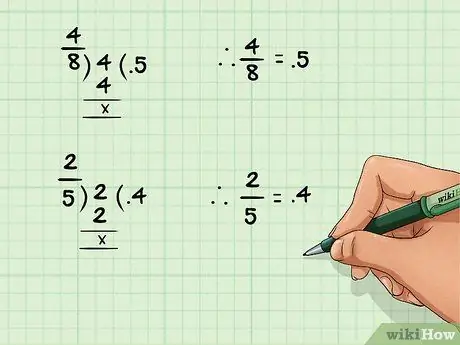
Step 1. Divide the numerator by the denominator to convert the fraction to a decimal
Define the dividing line between the numerator and denominator as "divided by". In other words, any fraction x/y can be interpreted as x divided by y.
For example: The fraction 4/8 returns the decimal number 0.5

Step 2. Determine the number of decimal points
Many numbers do not divide equally with each other. If you divide it, you must determine how many decimal places you need to give your answer. Often, the default is two decimal places. Remember the rounding rule when shortening a fraction: if the next number is 5, round up the previous number. For example, 0.145 is rounded to 0.15.
- For example: The fraction 5/17 returns the decimal number 0, 2941176470588…
- The last decimal number can be written as 0.29.
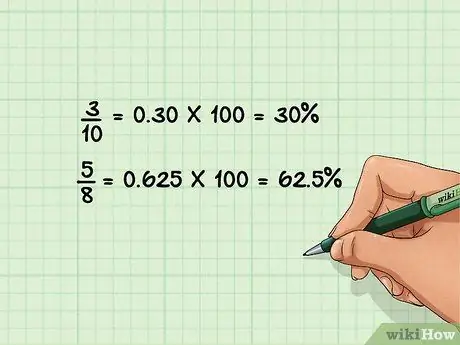
Step 3. Divide the fraction and then multiply by 100 to convert it to a percent
Just as you would convert a fraction to a decimal, divide the numerator by the denominator. Multiply the resulting decimal number by 100 and add the percent symbol (%) to end the conversion process.
- If you have 4/8, dividing 4 by 8 will give you 0.50, then multiplying that number by 100 will give you 50. Adding a percent sign (%) makes your final answer 50%.
-
Some additional examples:
- 3/10 = 0, 30 * 100 = 30%
- 5/8= 0, 625 * 100 = 62, 5%
Tips
- Knowing the time table will help you a lot.
- Beware that teachers generally know if someone has used a calculator. If (by the rules) you're not supposed to use a calculator, it's probably best not to.
- Many calculators have a fraction key. It may be possible to use a calculator to reduce fractions to their smallest form. For more details, read the calculator's manual.
Warning
- Make sure that the decimal point is in the right place.
- When converting from a fraction to a decimal, be sure to divide the numerator by the denominator.






