- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
If you already understand, converting ordinary fractions to decimals is not difficult. To convert common fractions to decimals, you can use long division, multiplication, or even a calculator if you don't want to calculate by hand. Once you've mastered the method, you'll be able to easily convert fractions to decimals.
Step
Method 1 of 4: With Long Division
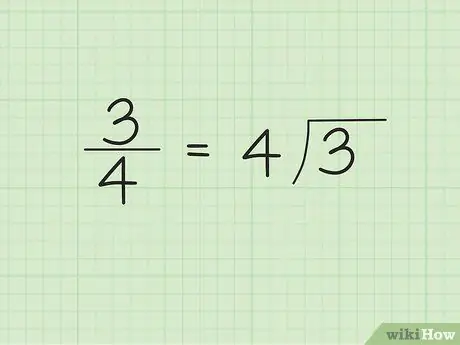
Step 1. Write the denominator outside/left side of the divisor symbol and the numerator inside/right side of the divisor symbol
For example, let's say we want to convert 3/4 to a decimal. Write “4” on the outside/left side of the divisor symbol and “3” inside/right side of the divisor symbol. “4” is the number that divides and “3” is the number that is divided.

Step 2. Write “0”, then a decimal point (a comma), above the divisor symbol
Since it's a fraction that counts, the result must be less than one, so this step is very important. After that, write the decimal sign, then “0”, after the number “3” in/right side of the divisor symbol. Even though “3” equals “3, 0”, the zero allows “3, 0” to be divided by “4”.

Step 3. Calculate the answer using long division
With long division, for now, the decimal sign can be ignored so you only need to calculate 30 divided by 4. Here's how:
- First, divide 3, 0, which counts as 30, by 4. The nearest 4 to 30 is 4 x 7 = 28, leaving 2. So write "7" after "0, " above the divisor and "28" under “3, 0” in/right side of the divisor symbol. Under 28, write "2", the remainder of 30 minus 28.
- Next, write “0” after “3, 0” so that it becomes “3, 00”, which can be considered as “300”, inside/right side of the divisor symbol. Thus, 0 can be lowered to the right of "2" so that "20" is divisible by "4".
- “20” divided by “4” equals “5”. So, write "5" after "0.7" above the divisor symbol so that it becomes "0.75".

Step 4. Write the final answer
So, “3” divided by “4” equals “0.75”. Write down the answer. Finished.
Method 2 of 4: Fractions Generating Repeating Decimals
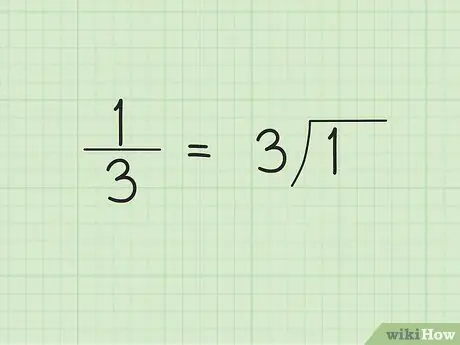
Step 1. Make long division division
When you start long-digit division, you may not be able to predict that the result will be a repeating decimal number. For example, let's say we want to convert the common fraction 1/3 to decimal form. Write 3, or the denominator, on the outside/left side of the divisor symbol and 1 inside/right side of the divisor symbol.

Step 2. Write a 0, then a decimal point, above the divisor symbol
Since the result must be less than 1, this step prepares the answer to be written in decimal form. The decimal sign must also be written to the right of the number “1” which is located in/right side of the divisor symbol.
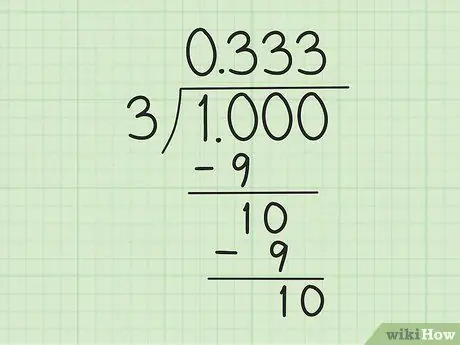
Step 3. Start calculating long division division
Start by making “1” into “1, 0”, which counts as “10”, so that it is divisible by “3”. Next, perform the following steps:
- Divide 10 by 3. Use 3 x 3 = 9 to make a remainder of 1. So write 3 to the right of the “0,” above the divisor and subtract 10 by 9 to get a remainder of 1.
- Write a "0" to the right of the number "1" (the remainder of 10 minus 9 in the previous step) below to get another "10". When again dividing “10” by “3”, the same process is repeated: write “3” to the right of the first “3” above the divisor symbol and subtract the new “10” by “9”.
- Continue until a pattern is formed. You know something's weird? This division can go on forever. 10 is always divisible by 3: there will always be a “1” at the bottom and a new “3” after the decimal above the divisor symbol.
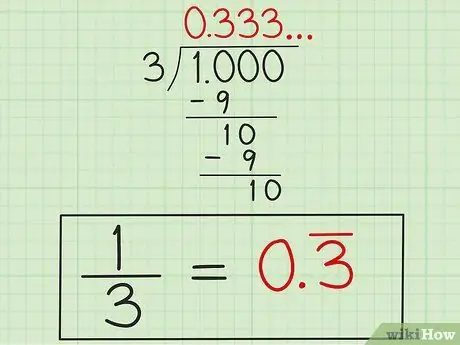
Step 4. Write the answer
After knowing that the "3" will repeat itself, write the answer as "0, 3" with a line above the number "3" (or "0, 33" with a line above the two "3") as an indication that the number "3" it keeps repeating. This answer is in the decimal form 1/3 because 1 divided by 3 will not end by itself.
There are many fractions that produce repeating decimals, such as 2/9 (“0, 2” with “2” repeating), 5/6 (“0, 83” with “3” repeating), or 7/9 (“0, 7” with “7” keeps repeating). This pattern always occurs when the denominator is a multiple of 3 and the numerator cannot be divisible by the denominator
Method 3 of 4: By Multiplication

Step 1. Find the number that can be multiplied by the fraction's denominator to produce 10, 100, 1,000, or any number that is base 10
This can be an easy way to convert fractions to decimals without using long division or a calculator. First, just find a number that can be multiplied by the fraction's denominator to get 10, 100, 1,000, and so on. To do this, first divide 10, then 100, then 1,000, and so on by the denominator until you get an integer. Example:
- 3/5. 10/5 = 2.2 is an integer. 2 can be multiplied by 5 to make 10. So 2 can be used.
- 3/4. 10/4 = 2, 5. 2, 5 is not an integer. 100/4 = 25. 25 is an integer. 25 can be multiplied by 4 to make 100. So 25 can be used.
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1,000/16 = 62, 5, 10,000/16 = 625. 625 is the first integer obtained. 625 can be multiplied by 16 to get 10,000. So, 625 can be used.
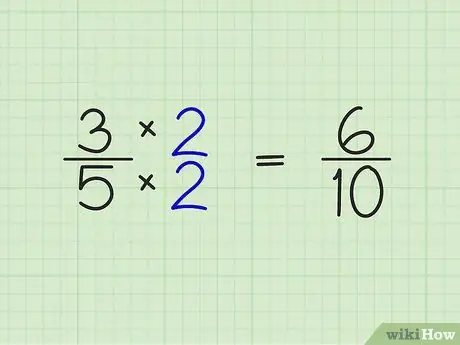
Step 2. Multiply the numerator and denominator of the fraction by the whole number obtained from the previous step
This step is quite easy. Just multiply the numbers above and below the fraction by the whole number you got in the previous step. Example:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3.125/10000

Step 3. Write the final answer
The answer is that the numerator is marked with a decimal according to the number of 0's in the denominator. Just count how many 0's are in the denominator. If there is only 1 0 in the denominator, move the decimal point to the left by 1 digit, and so on. Example:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Method 4 of 4: With Calculator

Step 1. Divide the numerator by the denominator
This method is very easy. Just use a calculator to divide the numerator, the number at the top of the fraction, by the denominator, the number at the bottom of the fraction. For example, say you want to convert 3/4 to a decimal. Just hit “3”, then the division symbol ("÷'"), then "4", and finally the equals symbol ("=").

Step 2. Write down the answers you get
The answer is 0.75. So, the decimal form of the common fraction 3/4 is 0.75.
Tips
- To check if your answer is correct, multiply the answer by the denominator of the fraction. If your answer is correct, the product of the multiplication is the numerator of the fraction.
- Some fractions can be converted to decimals by creating comparable fractions whose denominators are base 10 (10, 100, 1,000, and so on). Next, use place values to write down the correct decimal form.






