- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
Dividing fractions by fractions may seem confusing at first, but it's actually really easy. All you have to do is flip, multiply and simplify! This article will walk you through the process and show you how easy it is to divide a fraction by a fraction.
Step
Part 1 of 2: Understanding How to Divide Fractions by Fractions
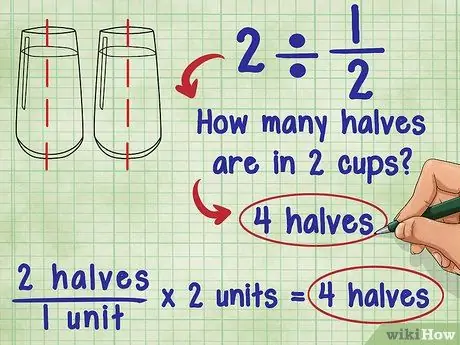
Step 1. Think about what dividing by a fraction means
About 2 ÷ 1/2 asked Ada: "How many half are in 2?" The answer is 4 because each unit (1) consists of two “half”, and there are 2 total units: 2 “half”/1 unit * 2 units = 4 “half”.
- Try imagining the same equation using a glass of water: How many and a half glasses of water are in 2 glasses of water? You can pour 2 and a half glasses of water into each glass of water. That means, basically, you add up the “half” glasses of water, and you have two glasses: 2 “half”/1 cup * 2 cups = 4 “half”.
- This means that if the fraction you are dividing is between 0 and 1, the answer is always greater than the original number! This is true when you divide a whole number or fraction by a fraction.

Step 2. Understand that dividing is the opposite of multiplying
Thus, dividing by a fraction can be solved by multiplying by the reciprocal of the fraction. The reciprocal of a fraction (also called the “multiplication inverse”) is the fraction that is inverted, so that the numerator and denominator swap places. In a moment, we'll be dividing fractions by fractions, by finding the reciprocal of the second fraction and multiplying both fractions. But let's look at some of the opposites first:
- The reciprocal of 3/4 is 4/3.
- The opposite of 7/5 is 5/7.
- The reciprocal of 1/2 is 2/1 or 2.
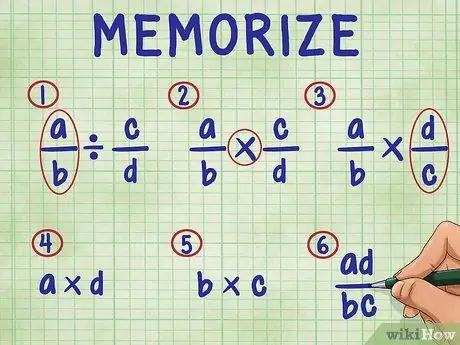
Step 3. Remember the following steps to divide a fraction by a fraction
In order, the steps include:
- Just leave the first fraction in the equation.
- Change the division sign to the multiplication sign.
- Invert the second fraction (find its reciprocal).
- Multiply the numerator (top number) of both fractions. The multiplication result is the numerator (top) of your answer.
- Multiply the denominator (bottom number) of both fractions. The product of the product is the denominator of your answer.
- Simplify your fractions by simplifying them to their simplest terms.

Step 4. Perform these steps for the 1/3 2/5 example
We'll start by leaving out the first fraction, and converting the division sign to the multiplication sign:
- 1/3 ÷ 2/5 = Becomes:
- 1/3 * _ =
- Now, we reverse the second fraction (2/5) to find its reciprocal, which is 5/2:
- 1/3 * 5/2 =
- Now, multiply the numerator (top number) of both fractions, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Now, multiply the denominator (bottom number) of both fractions, 3*2 = 6.
- Now, we have: 1/3 * 5/2 = 5/6
- This fraction cannot be simplified any further, so we have our answer.

Step 5. Try to remember the following rhymes to help you remember:
"Dividing fractions is easy, reverse the second fraction, then multiply. Don't forget to simplify before it's time to eat."
Another helpful reminder help tells you what to do with each part of the equation: “Let Me (first fraction), Change Me (division sign), Invert Me (second fraction).”
Part 2 of 2: Dividing Fractions by Fractions in Problems
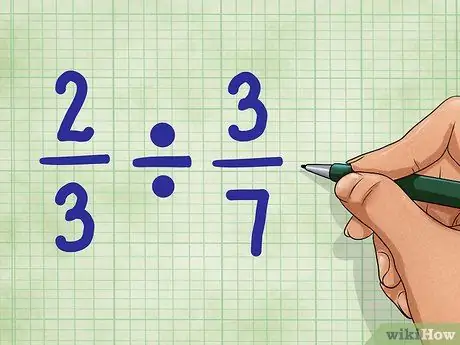
Step 1. Start with sample questions
Let's use 2/3 ÷ 3/7. This question asks for the number of parts equal to 3/7, which can be found in the value 2/3. Do not worry. It's not as difficult as it sounds!
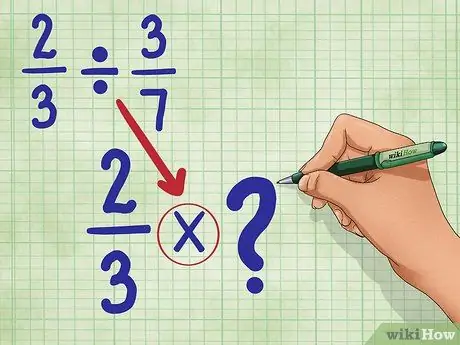
Step 2. Convert the division sign to the multiplication sign
Your new equation will be: 2/3 * _ (We'll be filling this blank in a moment.)
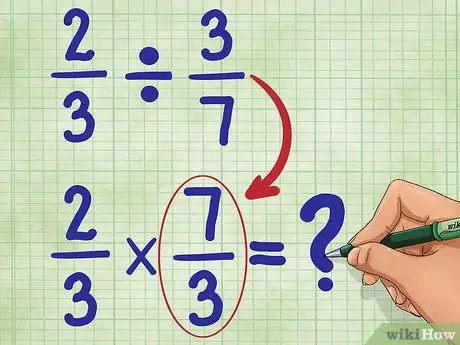
Step 3. Now, find the reciprocal of the second fraction
This means flipping 3/7 so that the numerator (3) is now at the bottom, and the denominator (7) is now at the top. The reciprocal of 3/7 is 7/3. Now, write your new equation:
2/3 * 7/3 = _

Step 4. Multiply your fractions
First, multiply the numerators of both fractions: 2 * 7 = 14. 14 is the numerator (top number) of your answer. Then, multiply the denominators of both fractions: 3 * 3 = 9. 9 is the denominator (bottom number) of your answer. Now, you know that 2/3 * 7/3 = 14/9.
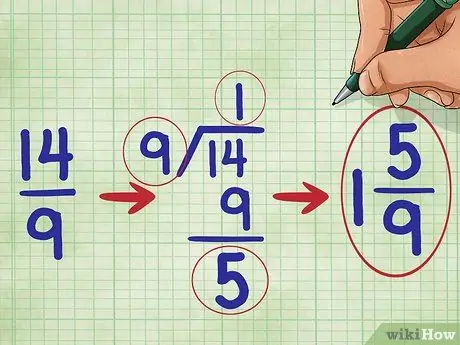
Step 5. Simplify your fraction
In this problem, because the numerator of the fraction is greater than the denominator, we know that our fraction is greater than 1. We must convert it to a mixed number. (A mixed number is a whole number and a fraction combined, for example 1 2/3.))
-
First, divide the numerator
Step 14. with 9.
The number 14 divided by 9 equals one with a remainder of 5, so you should write down your simplified fraction as: 1 5/9 (“one five-nineth”).
- Stop, you've found the answer! You can specify that you cannot simplify the fraction anymore because the denominator is not divisible by the numerator (9 is not divisible by 5) and the numerator is a prime number, or an integer that is only divisible by one and the number itself.
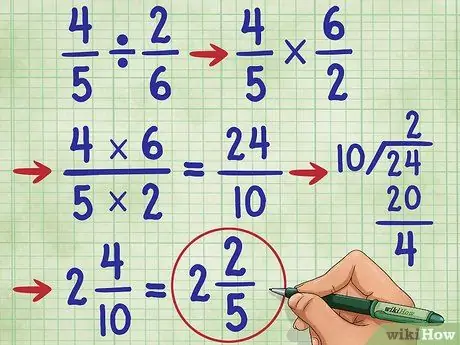
Step 6. Try another example
Let's try the question 4/5 ÷ 2/6 =. First, change the division sign to the multiplication sign (4/5 * _ =), then find the reciprocal of 2/6, which is 6/2. Now, you have the equation: 4/5 * 6/2 =_. Now, multiply the numerator, 4 * 6 = 24, and the denominator 5* 2 = 10. Now, you have 4/5 * 6/2 = 24/10.
Now, simplify the fraction. Since the numerator is greater than the denominator, we must convert this fraction to a mixed number.
- First, divide the numerator by the denominator, (24/10 = 2 remaining 4).
- Write the answer as 2 4/10. We can still simplify this fraction again!
- Note that 4 and 10 are even numbers. So, the first step to simplifying it is to divide each number by 2. We get 2/5.
- Since the denominator (5) is not divisible by the numerator (2) and 5 is a prime number, we know that this fraction cannot be simplified any further. So, our answer is: 2 2/5.

Step 7. Get additional help simplifying fractions
You probably spent a lot of time learning how to simplify fractions before trying to divide them by each other. However, if you need a refresher or some other help, there are some great online articles that can be of great help to you.
Related wikiHow Articles
- Converting Common Fractions to Decimals
- Calculating the Area of a Circle
- Dividing Polynomials Using Synthetic Division
- Dividing Mixed Fractions






