- Author Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:11.
- Last modified 2025-01-23 12:04.
Everyone can learn Math whether they are already at a higher stage in school or who just want to hone the basics again. After discussing how to be a good learner in Maths, this article will teach you the basic math progressions and will give you the basic elements you'll need to learn in each practice. Then, this article will discuss the basics of learning arithmetic, which will help both elementary school children and everyone who wants to learn the basics of this field of science.
Step
Part 1 of 6: Keys to Becoming a Good Math Student

Step 1. Appear in class
When you miss class, you should learn concepts from classmates or from your textbook. You'll never get a text summary from a friend as much as you get from your teacher.
- Come to class on time. In fact, arrive a little early and open your notebook in the right place, open your textbook and take out your calculator so you're ready to start when your teacher is ready to teach.
- Only truant if you are sick. If you really miss class, ask your classmates to find out what the teacher was talking about and what homework was given.

Step 2. Work with your teacher
If your teacher is working on a problem in front of the class, work with the teacher by working on the problem in your notebook.
- Make sure your notes are clear and easy to read. Don't just write questions. Also write down anything the teacher says that can improve your understanding of the concepts being explained.
- Complete the sample questions given by your teacher. As the teacher walks around the class as you work, answer the questions that are asked.
- Participate when the teacher solves a problem. Don't wait for the teacher to call you. Offer to answer when you know the answer, and raise your hand to ask a question if you are unsure of the material being taught.

Step 3. Do your homework on the same day your homework is given
If you do your homework on the same day, the concept is still fresh in your mind. Sometimes, finishing your homework on the same day is not possible. Make sure your homework is done before you go to class.

Step 4. Work outside of class if you need help
Visit your teacher during breaks or during office hours.
- If you have a Math Center at your school, find out its opening hours and ask for help.
- Join a study group. A good study group generally consists of 4 or 5 people with different levels of ability. If you are a "C" student in Maths, join a group of 2 or 3 students with "A" or "B" grades so you can improve your skills. Avoid joining a group of students whose grades are lower than yours.
Part 2 of 6: Learning Maths in School

Step 1. Start with arithmetic
In most schools, students learn arithmetic in elementary school. Arithmetic covers the basics of addition, subtraction, multiplication and division.
- Do practice questions. Doing arithmetic problems over and over is the best way to memorize the basics correctly. Look for software that can give you a wide variety of different Math problems to work with. Also, look for problems with timeframes to improve your speed.
- You can also find arithmetic problems online, and you can download arithmetic apps to your mobile device.

Step 2. Continue with the pre-algebra
This exercise will provide you with the basic elements you will need to solve algebra problems later on.
- Learn about fractions and decimals. You'll learn to add, subtract, multiply, and divide fractions and decimals. Regarding fractions, you will learn how to subtract fractions and translate combined numbers. Regarding decimals, you will understand place values, and you will be able to use decimals in story problems.
- Learn about ratios, proportions and percentages. These concepts will help you learn to make comparisons.
- Introduce yourself to basic geometry. You will learn 3D shapes and concepts. You'll also learn concepts like area, perimeter, volume and surface area, as well as information about parallel and perpendicular lines and angles.
- Understand some basic statistics. In pre-algebra, your introduction to statistics generally includes visuals such as graphs, scatter charts, stamp plot charts and histograms.
- Learn the basics of algebra. This includes concepts such as solving simple equations containing variables, learning about properties such as the distributive property, drawing simple equations, and solving inequalities.
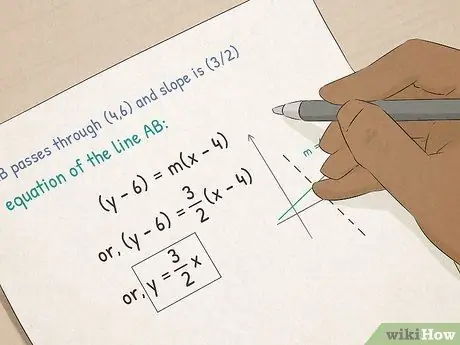
Step 3. Advance to Algebra I
In your first year of algebra, you will learn about the basic symbols included in algebra. You will also learn to:
- Solve equations and inequalities containing variables. You will learn how to solve these problems on paper and how to solve them with pictures.
- Solve story problems. You will be surprised how many everyday problems you will face in the future that require the ability to solve algebraic story problems. For example, you would use algebra to find out the interest rate you earn on your bank account or investment. You can also use algebra to figure out how long you should travel based on the speed of your car.
- Work with exponents. When you start solving polynomial equations (expressions that contain numbers and variables), you'll understand how to use exponents. This will probably include exercises with scientific notation. Once you master exponents, you can learn to add, subtract, multiply and divide polynomial expressions.
- Solve square and square root problems. As you master this topic, you will be able to memorize the squares of many numbers. You will also be able to work with equations that have square roots.
- Understand functions and graphs. In algebra, you will learn about graphic equations. You'll learn how to calculate the slope of a line, how to put an equation in point-slope form, and how to calculate the x-and-y slice of a line using the slope-intercept form.
- Find out the system of equations. Sometimes, you are given 2 different equations with the variables x and y, and you have to solve for x or y for both equations. Luckily, you'll learn a lot of tricks for solving these equations including graphing, substitution and addition.

Step 4. Study geometry
In geometry, you will learn about the properties of lines, segments, angles and shapes.
- You will memorize a number of theorems and corollaries that will help you understand the rules of geometry.
- You will learn how to calculate the area of a circle, how to use the Pythagorean theorem and how to find the relationship between the angles and sides of a special triangle.
- You will see many geometry questions in future standardized tests such as the SAT, ACT and GRE.
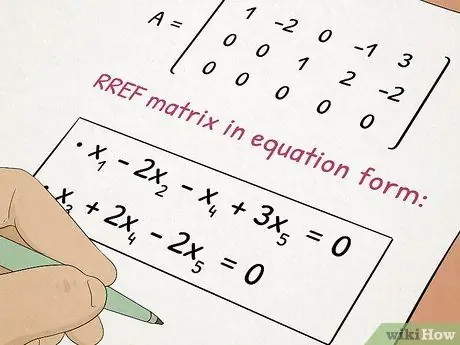
Step 5. Take Algebra II class
Algebra II builds on the concepts you've learned in Algebra I while adding to complex topics such as quadratic equations and matrices.
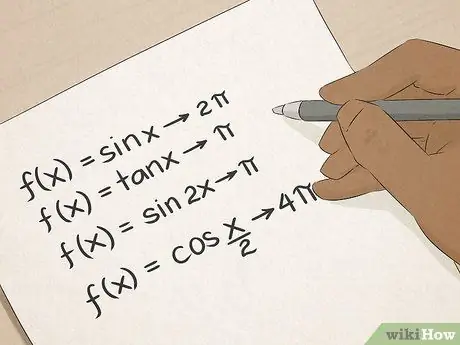
Step 6. Master trigonometry
You know trigonometric terms: sine, cosine, tangent, and so on. Trigonometry will teach you many practical ways to calculate angles and line lengths, and these skills will be invaluable to people working in construction, architecture, engineering or surveying.
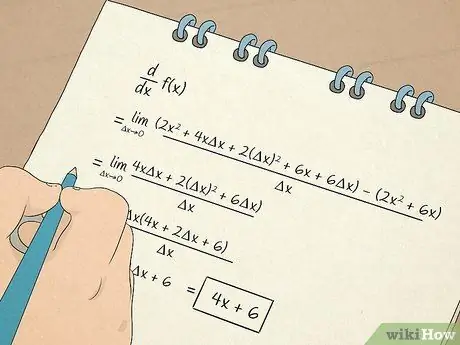
Step 7. Perform calculus calculations
Calculus may sound intimidating, but it is a wonderful tool for understanding either the behavior of numbers or the world around you.
- Calculus will teach you functions and limits. You will see the number behavior of useful functions including e^x and logarithmic functions.
- You will also learn how to calculate and work with derivatives. The first derivative gives you information based on the slope of the tangent line to an equation. For example, a derivative tells you the rate at which something changes in a non-linear situation. The second derivative will tell you whether the function increases or decreases over a certain interval so you can determine the concavity of a function.
- Integrals will teach you how to calculate the area under a curve as well as its volume.
- Calculus in high school generally ends in sequences and sequences. Although students will not see many applications for circuits, circuits are important for those studying differential equations.
Part 3 of 6: Math Fundamentals--Master Addition

Step 1. Start with "+1" facts
Adding 1 to a number takes you to the highest number on the number line. For example, 2 + 1 = 3.
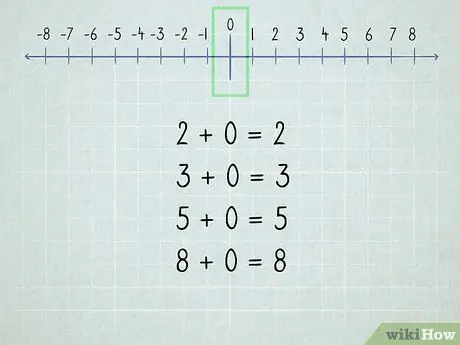
Step 2. Understand the zero
All numbers added to zero are the same number because "zero" means "none."

Step 3. Learn double numbers
Multiple numbers is a problem that involves adding two equal numbers. For example, 3 + 3 = 6 is an example of an equation involving multiple numbers.

Step 4. Use mapping to learn about other addition solutions
In the example below, you learn by mapping what happens when you add 3 to 5, 2 and 1. Try the "add by 2" problem yourself.

Step 5. Continue until the number is more than 10
Learn to add 3 numbers together to get a number greater than 10.
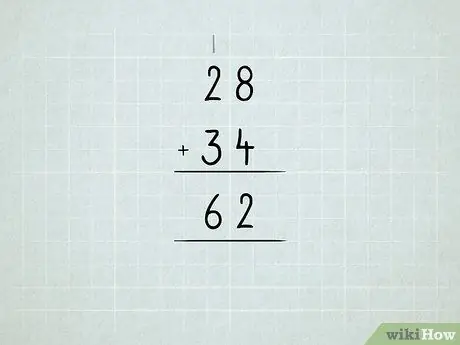
Step 6. Add up the larger numbers
Learn about regrouping units into tens, tens into hundreds, and so on.
- Add up the numbers in the column to the right first. 8 + 4 = 12, which means you have 1 number 10 and 2 number 1. Write the number 2 under the units column.
-
Write the number 1 in the tens column.
-
Add up the tens column in its entirety.
Part 4 of 6: Mathematical Fundamentals--Reduction Strategies

Step 1. Start with "backward 1 digit
Subtracting 1 from a number takes you back 1 number. For example, 4 - 1 = 3.

Step 2. Learn to subtract double numbers
For example, you add the numbers 5 + 5 to get 10. Just write the equation backwards to get 10 - 5 = 5.
- If 5 + 5 = 10, then 10 - 5 = 5.
-
If 2 + 2 = 4, then 4 - 2 = 2.

Step 3. Memorize the fact family
As an example:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Step 4. Find the missing numbers
For example, _ + 1 = 6 (the answer is 5).

Step 5. Memorize the fact of subtraction to 20

Step 6. Practice subtracting 1-digit numbers from 2-digit numbers without borrowing
Subtract the numbers in the ones column and decrease the numbers in the tens column.
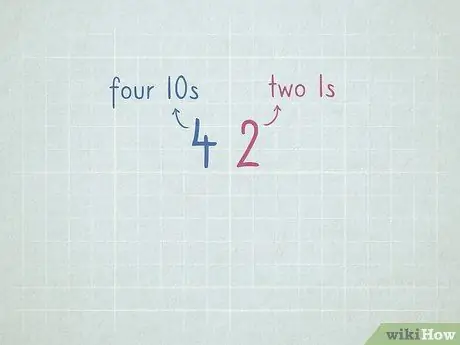
Step 7. Practice place value to prepare for subtracting by borrowing
- 32 = 3 numbers 10 and 2 numbers 1.
- 64 = 6 digits 10 and 4 digits 1.
- 96 = _ number 10 and _ number 1.
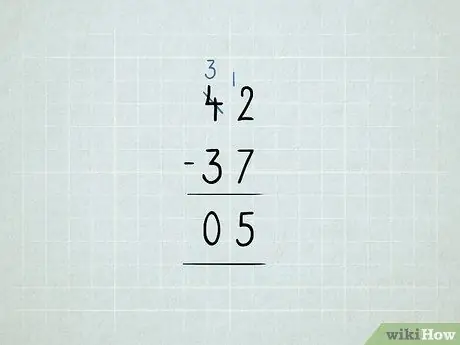
Step 8. Subtract by borrowing
- You want to subtract 42 - 37. You start by trying to subtract 2 - 7 in the units column. Turns out, it didn't work!
-
Borrow the number 10 from the tens column and place it in the ones column. Now you have 3 10's instead of 4 10's. Now you have 12 1's instead of 2 1's.
-
Subtract your units column first: 12 - 7 = 5. Then, check the tens column. Since 3 - 3 = 0, you don't need to write down the number 0. Your answer is 5.
Part 5 of 6: Math Basics--Master Multiplication

Step 1. Start with the number 1 and the number 0
All numbers that are multiplied by 1 are the same as the number itself. Any number multiplied by 0 is equal to zero.

Step 2. Memorize the multiplication table

Step 3. Practice with single digit multiplication problems

Step 4. Multiply the 2-digit number by the 1-digit number
- Multiply the bottom right number by the top right number.
-
Multiply the bottom right number by the top left number.
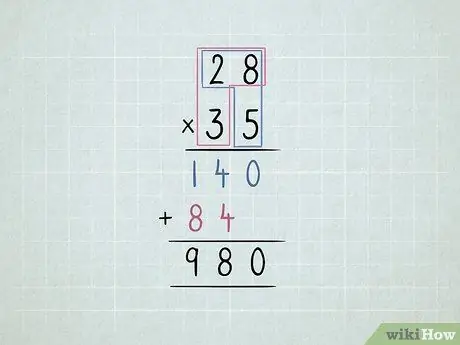
Step 5. Multiply 2 2-digit numbers
- Multiply the bottom right number by the top right number and then by the top left number.
-
Move the second row one digit to the left.
- Multiply the bottom left number by the top right number and then the top left number.
-
Add up all the columns.
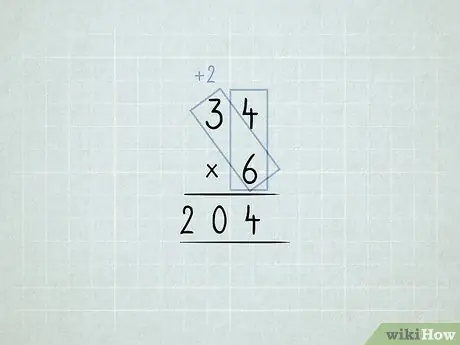
Step 6. Multiply and regroup the columns
- You want to multiply 34 x 6. You start by multiplying the units columns (4 x 6), but you can't have 24 1s in the ones column.
-
Store 4 1s in the units column. Move 2 10s to the tens column.
-
Multiply 6 x 3, which equals 18. Add the 2 you moved, which equals 20.
Part 6 of 6: Mathematical Fundamentals--Reveal Division Problems

Step 1. Think about division as opposed to multiplication
#* If 4 x 4 = 16, then 16 / 4 = 4.
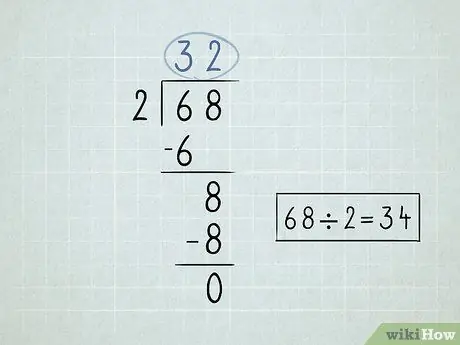
Step 2. Write down your division problem
- Divide the number to the left of the division symbol, or divisor, by the first number below the divisor symbol. Since 6 / 2 = 3, you would write the number 3 above the division symbol.
-
Multiply the number above the division symbol by the divisor. Bring the result down to the bottom of the first number under the division symbol. Since 3 x 2 = 6, then you will lower the number 6 down.
- Subtract the 2 numbers you have written down. 6 - 6 = 0. You can leave 0 blank, because you generally don't start numbers with 0.
-
Bring down the second number that is below the division symbol.
- Divide the number you bring down by the divisor. In this case, 8 / 2 = 4. Write the number 4 above the division symbol.
-
Multiply the top right number by the divisor and bring the number down. 4 x 2 = 8.
-
Subtract those numbers. The final subtraction returns zero, which means you've solved the problem. 68 x 2 = 34.

Step 3. Also calculate the remainder
Some of the divisors are not fully divided into other numbers. If you have completed the last subtraction, and you have no more numbers to derive, then the last number is the remainder.






