- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-01-23 12:04.
The billiard balls hit each other with perfect elasticity. That is, the kinetic energy of motion is almost completely preserved, and very little of it is converted to heat or other energy. This makes billiards an interesting sport to be analyzed mathematically. If you have complete control over how you poke the white ball and where it goes, you'll always be able to predict what's going to happen.
Step
Part 1 of 3: Predicting the Ball's Bounce Angle on Rail
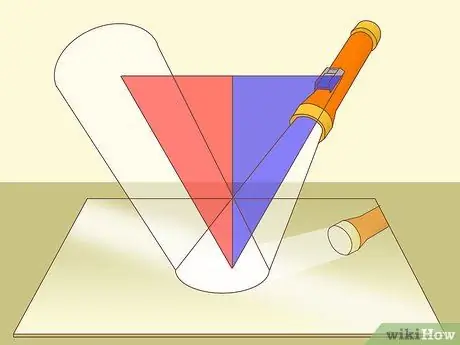
Step 1. Understand the law of reflection
Many pool players already know this simple math because it is needed every time they want to bounce the ball on the rails (cushioned edges on the pool table). This law states that the angle of incidence of the reflection is equal to the angle of departure. This means that if the ball hits the rail at an angle of 30º, the bounce angle will also be 30º.
The law of reflection originally referred to the nature of light. Usually, this law reads "The angle of incidence is equal to the angle of reflection."

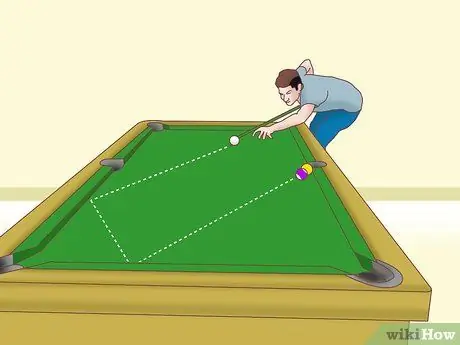
Step 2. Set the white ball and object ball the same distance to the rail
In this scenario, your goal is to bounce the white ball on the rail and hit the object ball. Now, try to apply the following basic geometry techniques:
- Draw a shadow line from the white ball that is perpendicular to the rail. This is the first line.
- Then, imagine the path of the white ball's reflection towards the rail. This line is the hypotenuse (hypotenuse) of a right triangle formed from the first line and rail.
- Now, imagine the white ball bouncing off the rail and hitting the object ball. Suppose there is a second right triangle on the object sphere that is symmetrical to the first triangle.

Step 3. Prove that these two triangles are congruent
In this case, we can use the "Side Angle" rule. If both triangles have two equal angles, and one side is the same (in the same configuration), then the two triangles are congruent. (In other words, the shape and size are the same). We can prove whether these two triangles on the pool table satisfy these conditions:
- The law of reflection states that the two angles between the hypotenuse and the rail have the same measure.
- Both are right angles so each has an angle of 90º.
- Since the two balls are the same distance from the rail, the two sides between the ball and the rail are the same length.
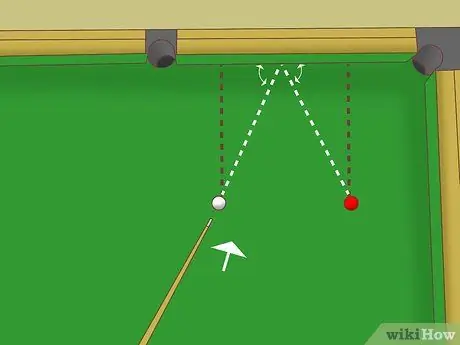
Step 4. Aim for the midpoint of the rail
Since these two triangles are congruent, the lengths of the sides on the rails are also equal to each other. That is, the distance from the bounce point to the two balls is the same. Aim for the midpoint if the white ball and the object ball are the same distance from the rail.
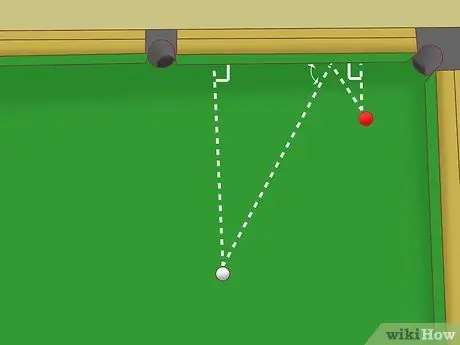
Step 5. Use a similar triangle if the white ball and object ball are not the same distance from the rail
Say the distance of the white ball to the rail is twice the distance of the object ball to the rail. You can still imagine the two right triangles formed by the ideal path of the white ball, and use your geometric intuition to aim:
- The two triangles still have the same angles, but different side lengths. That is, the two triangles are still similar: the shape is the same, but the size is different.
- Since the white ball is twice as far from the rail, the first triangle is twice as large as the second triangle.
- That is, the rail side of the first triangle is twice as long as the rail side of the second triangle.
- In this case, aim for a point on the rail at the distance from the object ball because is twice.
Part 2 of 3: Calculating the Angle of Impact of Ball Objects

Step 1. Learn the basics
Most kicks in billiards are corner shots or "cuts", which means the white ball doesn't hit the object directly. The more "thinner" the ball hits, the greater the angle of the object's ball path, depending on the white ball's trajectory.
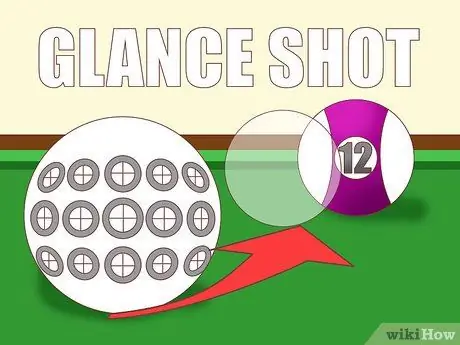
Step 2. Estimate the fullness of the impact
A good way to estimate this effect is to monitor the impact against the ball's planned trajectory. When the balls collide, how much does the white ball "overlap" on the object ball from your perspective? The answer will show how "full" the ball hit:
- Dead ons completely overlap. You could say the level of "fullness" is 1.
- If the white ball covers of the object's balls, it means that the collision of the balls is full.
Step 3. Estimate the angle based on the degree of fullness
The graphs of these two quantities are not quite linear, but close enough that you can estimate them by adding 15º each time you subtract fullness. Otherwise, you can use the following measurements which are more accurate:
- Direct impact (1st degree of fullness) results in a 0º cut angle. The object ball completely continues the path of the white ball.
- A full impact sends the object ball at an angle of 14.5º.
- A full impact sends the object ball at an angle of 30º.
- A full collision sends the object ball at an angle of 48, 6º.
Step 4. Be careful when shooting thin
If you want to hit the ball at a fullness less than, it is difficult to estimate the number of balls covered. What's more, the impact of the cut angle is so drastic that a small error will greatly change the resulting angle. This tangent shot takes a lot of practice and works well once you know the point you're aiming for. If you can, find another shot to take.
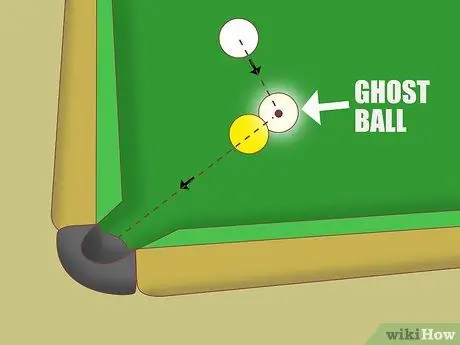
Step 5. Try applying the ghost ball method for aiming
If the impact fullness description doesn't help you, try the “ghost ball” approach:
- Imagine there is a straight line from the table pocket to the center of the object ball.
- Extend this line slightly past the object ball. Imagine that there is a “ghost ball” at this point, being on the line and touching the object ball.
- To knock the object ball into the pocket, you need to aim at the center of the "ghost ball".
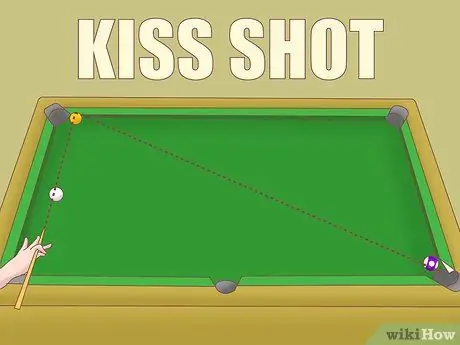
Step 6. Apply the rule of three kiss shots
A peck shot is done by hitting a white ball against ball A so that it aims and hits ball B. If you're playing a game where kisses are allowed, keep this rule in mind: if ball A hits the rail, the cut angle you aim for is the angle made by the three balls.
For example, if the angle with sphere A as the vertex is 45º, the cut angle is about 15º. The fullness rule above states that this angle can be produced with a full collision
Part 3 of 3: Using English (Side Twist)
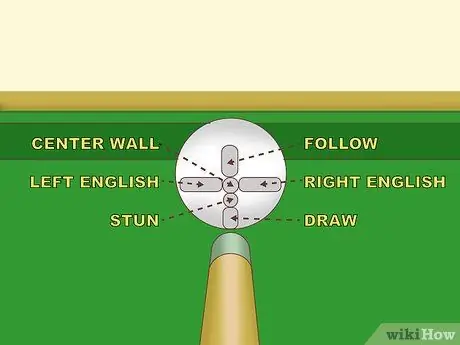
Step 1. Perfect your poke first
A poke with a consistent attitude and aim should be a top priority if you want to play pool seriously. English is a very useful technique, but its effects are complex and you need to practice it consistently.
You'll have a hard time narrowing the impact of English if you don't take control of the overspin and slipping forces. This impact is determined by the height of the ball's thrust point. Slipping can be completely eliminated by hitting at a point the length between the center and the top of the ball, but it is common for players to hit at a point this distance for optimal control and speed
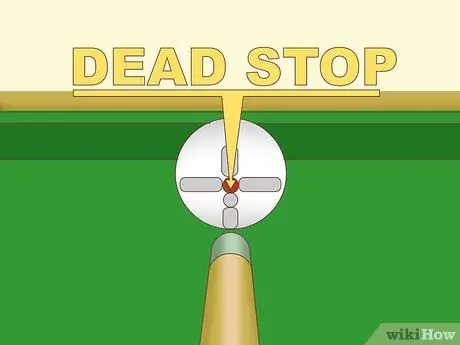
Step 2. Stay away from English when the white ball is in danger of entering the bag
Provided there is no English, the white ball will stop completely after a perfect direct impact. Practice direct impact by hitting exactly the center of the white ball's vertical and horizontal axes. Once you can get the white ball to stop completely each time, you should be skilled enough to include English in the game.
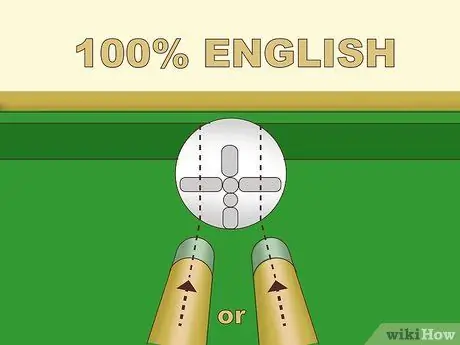
Step 3. Practice various English strengths
There are several types of English, but this article discusses only the basic forms. If the stick poked to the left of the ball's center, the ball would rotate along this axis; here's "English left". When this spinning ball hits the surface, the spin will make the ball turn more to the left than without English. Conversely, poking to the right of the center of the white ball will bring up "English right" and bounce the ball further to the right. The further you poke from the center of the ball, the bigger the impact:
- English 100% or maximum is done by poking the midpoint between the center and the edge of the ball. This is the maximum poke distance to get a poke with minimal error.
- English 50% is done by poke the midpoint between the maximum point and the center of the ball (¼ the distance between the center to the edge of the ball).
- You can use English percentages by poking at various points between the center and the maximum point of the white ball.
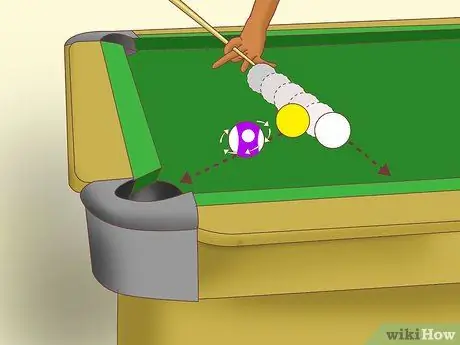
Step 4. Understand gearing
When two balls collide, the object ball begins to rotate on a certain axis, according to the angle of the stroke and the amount of English gained. If you can achieve " gearing ", this rotation occurs along the axis of motion. In other words, the motion of the object ball is not affected by rotation. The ball will slide along the “center line” or the line drawn between the centers of the two balls on impact.
The term comes from the analogy of two gears working smoothly with each other and transmitting motion perfectly
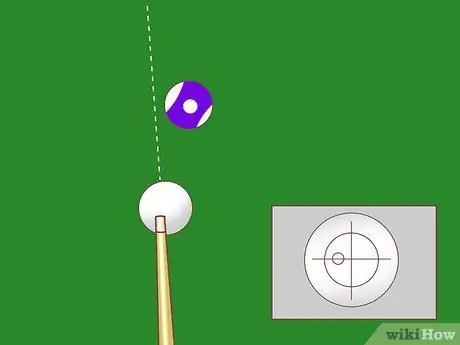
Step 5. Adjust the English to achieve gearing in all pieces
Once you've shot a corner using the "full" or "ghost ball" approach, it's a good idea to make sure the object ball doesn't spin weirdly and ruin your shot. Here's a chart that can help you find the right angle and English. All numbers below are " English outside " which means you move the stick next to the white ball further than the object ball.
- If the cut angle is 15º, use English slightly greater than 20%. (Remember, the cut angle is the angle between the white ball's initial path and the object's ball path.)
- If the cut angle is 30º, use English at 40%.
- If the cut angle is 45º, use 55% English.
- If the cut angle is 60º, use English at 70%.
- When the cut angle approaches 90º, increase the English to 80%.
Step 6. Know the effect of impact without gearing
If you use English less of the many "gearing" in the last step, the white ball will shift forward during the impact, and the side twist shifts to the object ball. Then, the object ball will move slightly to the right from the estimated cut angle. If your English is more than gearing, the object ball will move slightly to the left of the estimated cut angle.
- This effect is called a cut induced throw: the angle of the cut displaces the twist which causes the ball to roll slightly off course.
- You can use this technique to make shots that seem almost impossible. If your only shot is a little too far to the right, increase your English to get the ball into the pocket.
Tips
- If the object ball is stuck to the rail and you need to roll it along the rail towards the bag, always hit the rail first before touching the object ball. Thus, the white ball gives momentum to the rail, rather than towards it. (If the angle of impact exceeds 45º, you will need to use English.)
- The greater the angle of impact between the two balls, the less the transmitted momentum. This means you'll need to poke a little harder for thin cuts (cracks at extreme angles).
- After impact, the angle between the path of the white ball and the path of the object's ball must always equal 90º. Use this knowledge to prevent white balls from entering the bag. Note that extreme twisting can break this rule, and balls of different mass (eg on a common pool table in a cafe).






