- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
Subtraction is simply subtracting one number from another. It's easy to subtract one whole number from another, but subtraction can be tricky if you're subtracting fractions or decimals. Once you understand subtraction, you'll be able to use more complex math concepts, and be able to add, multiply, and divide numbers more easily.
Step
Method 1 of 6: Subtracting Large Whole Numbers by Borrowing

Step 1. Write down a large number
For example, you want to solve 32 - 17. Write down 32 first.

Step 2. Write the smaller number right below it
Make sure that you place the tens and ones values in the correct columns, so that 3 of 32 is directly above 1 of 17 and 2 of 32 is directly above 7 of 17.
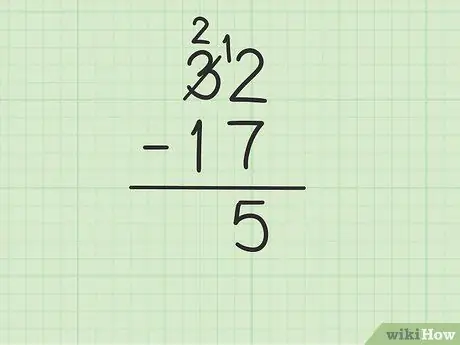
Step 3. Subtract the top number in the units column from the bottom number
However, this can get complicated if the bottom number is greater than the top number. In this case, 7 is greater than 2. Here's what you have to do:
- You have to borrow from 3 of 32 (also known as grouping), to turn 2 into 12.
- Cross the number 3 out of 32 and replace it with the number 2, while the number 2 becomes 12.
- Now you can subtract 12 - 7, which equals 5. Write 5 under the two numbers you are subtracting so that they are in the units column of the new row.
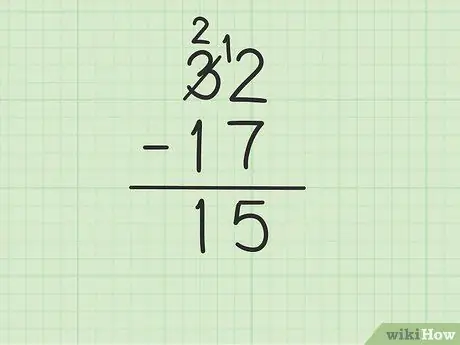
Step 4. Subtract the top number in the tens column from the bottom number
Remember that 3 has become 2. Now subtract the number 2 above by 1 from 17 to get (2-1) 1. Write 1 below, in the tens column, to the left of the number 5 in the units column. You write 15. That is, 32 - 17 = 15.
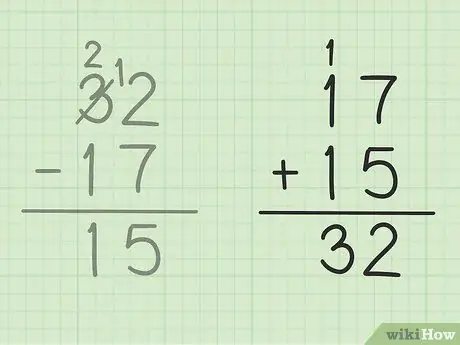
Step 5. Check your work
If you want to make sure you've subtracted two numbers correctly, then all you have to do is add up your answer with the smaller number to make a large number. In this problem, you have to add your answer, 15 to the smaller number of subtraction, 17. 15 + 17 = 32, so that your answer is correct. Safe!
Method 2 of 6: Subtract Small Whole Numbers
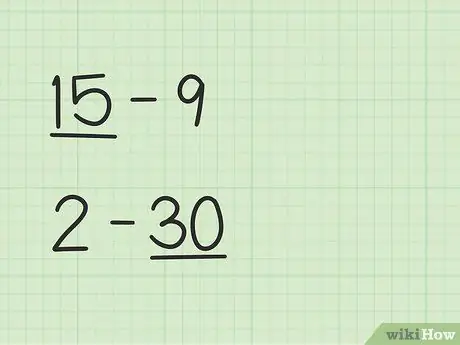
Step 1. Find the larger number
Problems like 15 -9 will have a different way than 2 - 30.
- In questions 15 - 9, the first number, 15, is greater than the second number, 9.
- In questions 2 - 30, the second number, 30, is greater than the first number, 2.

Step 2. Decide if your answer will be positive or negative
If the first number is greater, the answer is positive. If the second number is greater, the answer is negative.
- In the first question, 15 - 9, your answer is positive because the first number is greater than the second number.
- In the second question, 2 - 30, your answer is negative because the second number is greater than the first number.
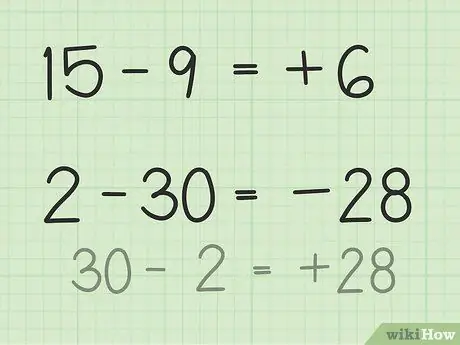
Step 3. Find the difference between two numbers
To subtract two numbers, you have to imagine the difference between the two numbers and calculate the numbers between them.
- For questions 15 - 9, imagine a stack of 15 poker chips. Throw away 9 chips and only 6. So, 15 - 9 = 6. You can also imagine a number line. Think of numbers from 1 to 15, then discard or return 9 units so you get 6.
- For questions 2 - 30, the easiest way to solve this is to invert the number and make the result negative after subtracting. So, 30 - 2 = 28 so 28 and 30 have a difference of 2. Now, make the result negative because you have already determined that the answer is negative because the second number is greater than the first number. So, 2 - 30 = -28.
Method 3 of 6: Subtracting Decimals
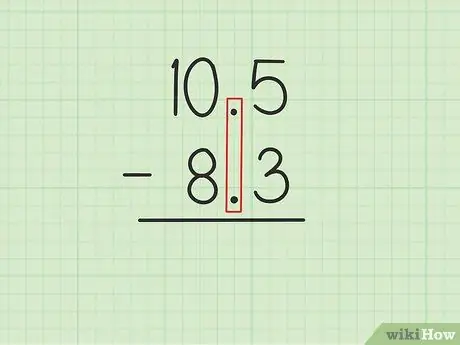
Step 1. Write the larger number over the smaller number with the decimal points aligned
Suppose you want to solve the following problems: 10, 5 - 8, 3. Write 10, 5 over 8, 3 so that the decimal points of the two numbers are parallel., 5 of 10, 5 must be directly above, 3 of 8, 3 and 0 of 10, 5 must be above 8 of 8, 3.
If you have a problem because the two numbers do not have the same number after the decimal point, write 0 in the blank until the sum of the numbers is the same. For example, the problem is 5, 32 - 4, 2, you can write it as 5, 32 - 4, 2 0. This won't change the value of the second number, but will make subtracting the two numbers easier.

Step 2. Subtract the top number in the tens column from the number below
In this case, you have to subtract 3 from 5. 5 - 3 = 2, so you have to write 2 under 3 of 8, 3.
Make sure you put a decimal point in the answer, so that it is written, 2

Step 3. Subtract the number above the units column from the number below it
You have to subtract 8 from 0. Borrow 1 from the tens part to change 0 to 10 and subtract 10 - 8 to get 2. You can also count 10 - 8 without borrowing because there are no numbers in the second tens column. Write the answer under 8, to the left of the decimal point.

Step 4. Write down your final result
Your final result is 2, 2.

Step 5. Check your work
If you want to make sure your decimal subtraction is correct, all you have to do is add up your answer with the smaller number to make the larger number. 2, 2 + 8, 3 = 10, 5, so you've finished.
Method 4 of 6: Subtract Fractions

Step 1. Align the denominator and numerator of the fraction
Suppose you want to solve problems 13/10 - 3/5. Write the problem so that the two numerators, 13 and 3 and the two denominators, 10 and 5 are opposite each other. These two numbers are separated by a subtraction sign. This will help you visualize the problem and solve it more easily.

Step 2. Find the least common denominator
The least common denominator is the smallest number that can be divided by two numbers. In this example, you have to find the smallest common denominator that is divisible by 10 and 5. You'll find that 10 is the smallest common denominator for both numbers because 10 is divisible by 10 and 5.
Note that the least common denominator of two numbers is not always one of them. For example, the smallest common denominator for 3 and 2 is 6 because 6 is the smallest number that can be divided by two numbers

Step 3. Write down the fractions using the same denominator
The fraction 13/10 can be written the same way because the denominator is 10, the smallest common denominator, which is 10, multiplied by 1. 2. So the fraction 3/5 must be multiplied by 2/2 to make the denominator 10, so 3/5 x 2/2 = 6/10. You have found the equivalent fraction. 3/5 is equivalent to 6/10 although 6/10 allows you to subtract the first number, 13/10.
Write a new question like this: 13/10 - 6/10
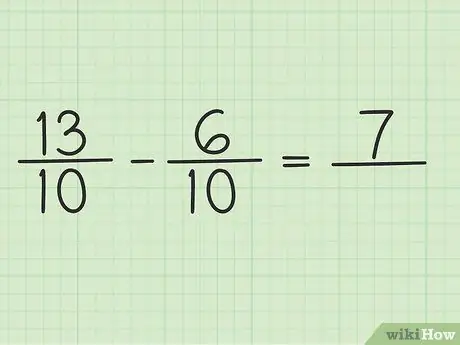
Step 4. Subtract the numerator to two numbers
Just subtract 13 - 6 so the result is 7. You can't change the denominator of the fraction.
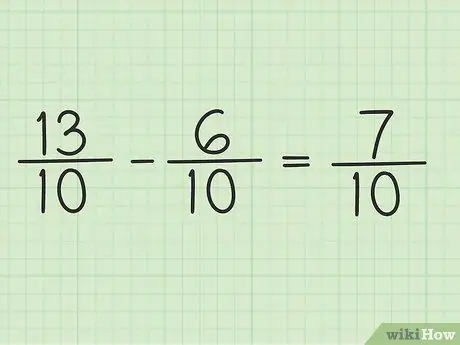
Step 5. Write the new numerator over the same denominator to get the final result
The new numerator is 7. Both fractions have a denominator of 10. Your final result is 7/10.
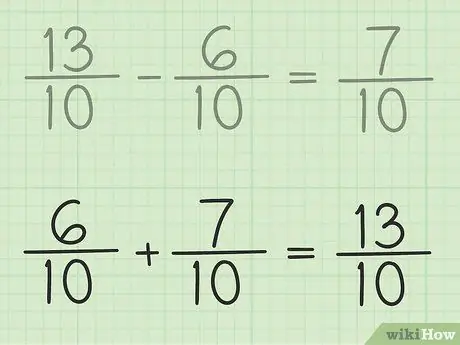
Step 6. Check your work
If you want to make sure you've subtracted the fraction correctly, just add up your answer and the smaller fraction so that the result is the larger fraction. 7/10 + 6/10 = 13/10. It's finished.
Method 5 of 6: Subtracting Fractions from Whole Numbers

Step 1. Write down the problem
For example, suppose you want to solve the following problem: 5 -. Write it down.
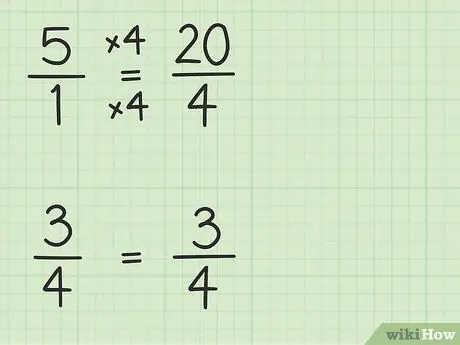
Step 2. Convert whole numbers into fractions that have the same denominator as other fractions
You'll be converting 5 to a fraction with a denominator of 4 to be able to subtract two numbers. So you need to think of 5 as a fraction of 5/1. Then, you can multiply the new fraction's numerator and denominator by 4 to make the two numbers' denominators the same. So 5/1 x 4/4 = 20/4. This fraction is equal to 5, but allows you to subtract two numbers.
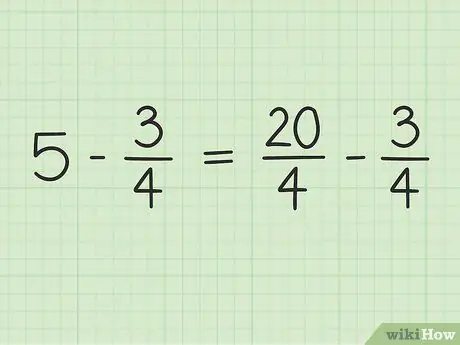
Step 3. Rewrite the problem
The new problem can be written like this: 20/4 - 3/4.

Step 4. Subtract the numerator of the fraction, while the denominator remains the same
Now, just subtract 20 by 3 to get the final result. 20 - 3 = 17, so 17 is the new numerator. You can leave the denominator the same.
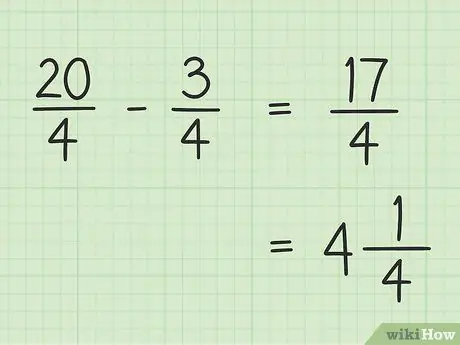
Step 5. Write down your final result
Your final result is 17/4. If you want to write it as a mixed number, divide 17 by 4 so that the result is 4 and the remainder is 1, so that your final 17/4 equals 4.
Method 6 of 6: Subtracting Variables

Step 1. Write down the problem you want to solve
For example the following question: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Write the first set of variables over the second.
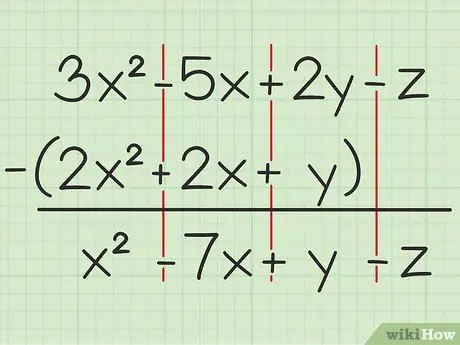
Step 2. Subtract the same variables
If you encounter a variable, you can only add or subtract the same variable and which is written with the same degree of squared. That means you can subtract 4x2 from 7x2, but cannot subtract 4x from 4y. So, you can break the problem down like this:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
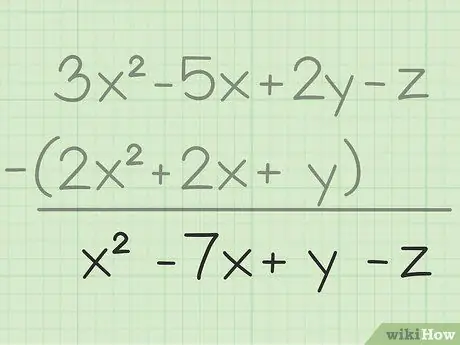
Step 3. Write down your final result
You've subtracted all the same variables, all you have to do is write your final result which will contain all the variables you've subtracted. Here is the end result:






