- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-01-23 12:04.
Students who are still very young often have difficulty understanding the concept of subtraction. If you are a teacher and want to teach the concept of subtraction to students, try to represent the concept in ways that are interesting and easier for students to understand. After explaining the basic concepts of subtraction, try moving on to the concept of two-digit subtraction. Once students have mastered it well, try explaining various concepts they can use to solve subtraction problems, such as Common Core.
Step
Method 1 of 4: Teaching Subtraction through Objects or Images

Step 1. Write or orally present a story problem containing a subtraction problem to students:
There are 8 oranges on the table, 3 oranges are eaten by Jordan. How many oranges are left?
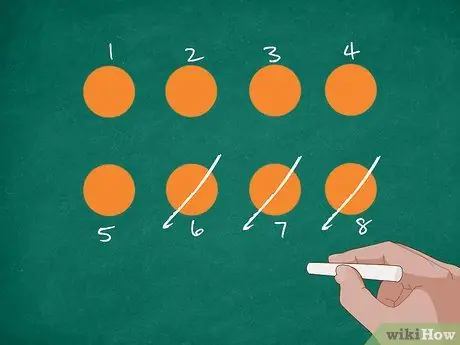
Step 2. Represent the problem with pictures
First, draw 8 orange circles on the board or a piece of paper. After that, have students count the number and label each circle with a number. Cross out 3 circles while explaining that Jordan ate 3 oranges. Ask students how many oranges are now left.
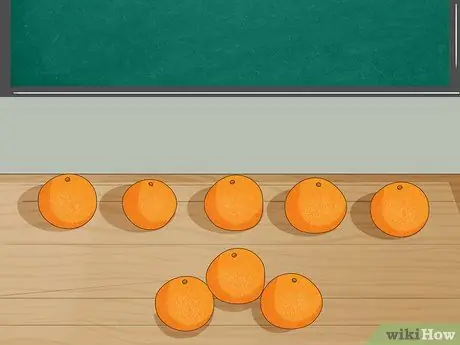
Step 3. Represent the problem with objects
Place 8 oranges on the table and ask students to count the number. After that, take 3 oranges from the table while explaining that Jordan ate 3 oranges. Have students count the number of oranges remaining.

Step 4. Write down the equation
Explain that story problems can also be represented through an equation. Make sure you always guide them in the process of turning story problems into math equations.
- Ask how many oranges are on the table. Write the number “8” on the board.
- Ask how many oranges Jordan ate. Write the number “3” on the board.
- Ask students if this is an addition or subtraction problem. Write a “-” sign between the numbers “8” and “3”.
- Have students look for answers to the equation “8-3.” Write down the “=” sign followed by the number “5.”
Method 2 of 4: Teaching Subtraction with the Countdown Method on the Number Line

Step 1. Write or orally present a story problem containing a subtraction problem to students:
There are 10 dogs in the pet shop, 6 of which have been adopted by their new owners. How many dogs are left in the pet shop?
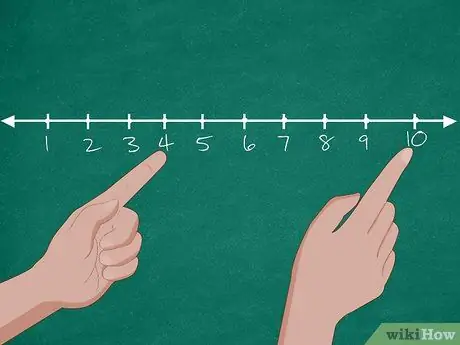
Step 2. Use the help of a number line to solve the problem
First, draw a number line containing the numbers 0-10 on the board. After that, ask students to name the number of dogs in the pet shop. After students answer, circle the number “10” on the board. Then, ask again how many dogs have been adopted. If students answer “6”, ask them to count down 6 numbers from 10 (9, 8, 7, 6, 5, 4) until they reach the number “4”. After that, ask again how many dogs are left at the pet store.

Step 3. Write down the equation
Explain that story problems can also be represented through an equation. Make sure you always guide them in the process of turning story problems into math equations.
- Ask how many dogs are there in the pet store. Write the number “10” on the board.
- Ask how many dogs were adopted. Write the number “6” on the board.
- Ask students if this is an addition or subtraction problem. Write a “-” sign between the numbers “10” and “6”.
- Have students look for answers to the equation “10-6.” Write an “=” sign followed by the number “4.”
Method 3 of 4: Teaching Subtraction through Fact Family Concepts

Step 1. Introduce the concept of fact family to students
In fact, a fact family is a group of mathematical problems consisting of the same numbers. For example, the numbers 10, 3, and 7 form a fact family. The three numbers can be added or subtracted in different ways; You can generate two equations using just these 3 numbers:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Step 2. Write or orally present a story problem containing a subtraction problem to students:
I have 7 candies. If I eat 3 candies, how many candies are left?

Step 3. Use the fact family concept to solve the problem
Guide students through the process step by step:
- Ask students what problem they would like to solve. Write "7-3=?" on the blackboard.
- Ask them to identify the third member of the fact family group. Write the following equations on the board: “3+_=7”; “_+3=7”; "; “7-_=3”; and 7-3=_” After that, ask students to read the results and fill in the problem with the answers they gave.
Method 4 of 4: Introducing Common Core Concepts

Step 1. Teach the concept of subtraction in Common Core
In fact, Common Core is a new learning standard that is applied by most states in America. In Common Core, the basic concept of subtraction is explained by the distance between two numbers. To explain the concept to students, try drawing a number line containing the numbers 1-10 on the board.
- After that, give a basic subtraction problem to students: 9-4=?.
- Find the location of the number 4 on the number line. Explain to students that the location is their starting point.
- Find the location of the number 9 on the number line. Explain to students that the location is the final destination.
- After that, ask students to measure or calculate the distance between the two numbers: “5, 6, 7, 8, 9.”
- The distance between the two numbers is 5. Thus, 9-4=5.
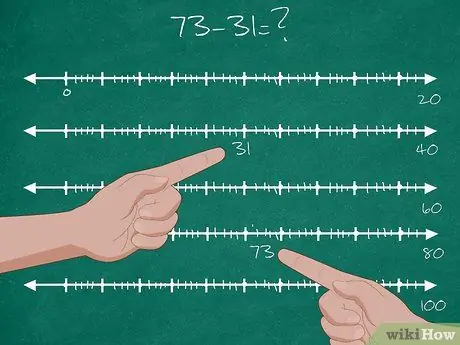
Step 2. Have students solve the two-digit subtraction problem
Explain to students that there will be two points that they must stop before arriving at their destination.
- Give students a two-digit subtraction problem: 73-31=?.
- Find the location of the number 31 on the number line. This is the starting point.
- Find the location of the number 73 on the number line. This is the end goal.
- “Stop” at the first tenth after 31. Thus, your first stop is 40. After that, measure the distance between 31 and 40, and write down the answer: 9.
- “Stop” at the tenths that are closer to 73. Thus, your second stop is 70. Then, measure the distance between 40 (first stop) and 70 (second stop), and write down the answer: 30.
- "Move" from 70 (second stop) to your final destination (73). Measure the distance between them and write down the answer: 3.
- Add these three results together: 9+30+3=42. Thus, 73-31=42.

Step 3. Have students solve the three-digit subtraction problem
When solving double-digit subtraction problems, explain to students that what will increase is not only the stopovers, but also the distance between each stopover.
- Give students a three-digit subtraction problem: 815-398=?.
- Find the location of the number 398 on the number line. This is the starting point.
- Find the location of the number 815 on the number line. This is the end goal.
- "Stop" at the first tenth after 398. Thus, your first stop is 400. Measure the distance between 398 and 400 and write down the answer: 2.
- "Stop" at the tenths that are closer to 815. So your second stop is 800. Measure the distance between 400 and 800, and write down the answer: 400.
- "Stop" at the tenths that are closer to 815. Thus, your third stop is 810. Measure the distance between 800 and 810, and write down the answer: 10.
- "Move" from the third stop to your final destination, which is the number 815. Measure the distance and write down the answer: 5.
- Add all the numbers you get: 2+400+10+5=417. Thus, 815-398-417.






