- Author Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- Last modified 2025-01-23 12:04.
All you need to calculate the average speed is the total displacement. or change of position, and total time. Remember that velocity also calculates the direction and speed of an object, so include a direction in your answer, such as "north," "front," or "left." If your speed calculation problem also involves constant acceleration, you can learn a quick way to find the answer even easier.
Step
Method 1 of 2: Calculating the Average Velocity of Displacement and Time

Step 1. Remember that velocity includes both the speed and direction of an object
Velocity describes the rate at which an object's position changes. This has to do not only with how fast the object is moving, but also with its direction. "100 meters per second southward" is a different speed value than "100 meters per second eastward."
- Quantities that have direction are called vector quantities'. This quantity can be distinguished from a directionless quantity called a scalar quantity by writing an arrow above the variable. For example, the notation v represents the rate, while the notation v → represents speed or speed + direction. The v notation used in this article represents speed.
- In scientific problems, you should use meters or other metric units to express distance, while for everyday purposes you can use any unit you like.

Step 2. Find the total displacement value
Displacement is the change in an object's position, or the distance and direction between its starting and ending points. The direction the object moves before reaching its final position can be neglected, because only the distance between the start and end points is taken into account. For the first example, we will use an object moving at a constant speed in one direction:
- Say a rocket is moving north for 5 minutes at a constant speed of 120 meters per minute. To calculate the final position, use the formula s = vt, or use practical thinking to calculate the distance traveled by the rocket after that (5 minutes)(120 meters/minute) = 600 meters north from the starting point.
- For problems involving constant acceleration, you can solve them with s = vt + at2, or use the short method described in another section to find the answer.
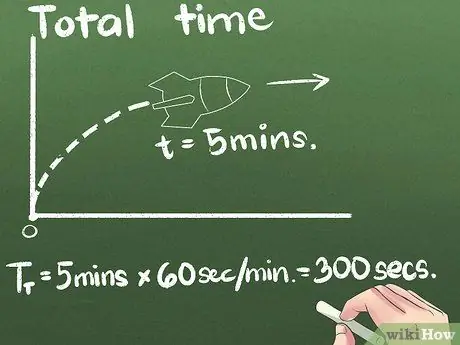
Step 3. Find the total time spent
In our example, the rocket is moving forward for 5 minutes. You can express the average speed in any unit of time, but the second is the international scientific standard unit. We will change the units of seconds in this example: (5 minutes) x (60 seconds/minute) = 300 seconds.
Even in scientific questions, if the question uses an hour or a larger unit of time, it will be easier to calculate the speed first, and then convert the final answer into meters/second

Step 4. Calculate the average velocity as displacement over time
If you know how far an object is moving, and how long it will take to get there, you will know how fast it is moving. So for the example we are using, the average speed of the rocket is (600 meters north) / (300 seconds) = 2 meters/second north.
- Remember to include a direction (such as "front" or "north").
- In the formula vav = s/Δt. The delta symbol means "change," so s/Δt means "change in position over a period of time."
- The average speed can be written as vav, or as a v with a horizontal line above it.

Step 5. Solve more complicated problems
If an object changes its direction or speed, don't get confused. Average speed is still "only" calculated from total displacement and total time. What happens between the start and end points you can ignore. The following are some examples of an object traveling with the same displacement and total time, and thus, the same average velocity:
-
Anna walks west at 1 meter/s for 2 seconds, then suddenly accelerates to 3 meters/second and continues walking west for 2 seconds. The total displacement is (1 m/s westward)(2 sec) + (3 m/s westward)(2 sec) = 8 meters westward. The total time is 2 seconds + 2 seconds = 4 seconds. So the average speed is 8 meters west/ 4 seconds = 2 meters/second west.
- Bart walks west at 5 meters/sec for 3 seconds, then turns around and walks east at 7 meters/sec for 1 second. We can think of the eastward movement as "negative westward motion" so the total displacement is = (5 meters/sec westward)(3 sec) + (-7 m/s westward)(1 sec) = 8 meters. Total time = 4 seconds. Average speed = 8 meters west / 4 seconds = 2 meters/second west.
-
Charlotte walked north 1 meter and then walked west 8 meters, then south 1 meter. The time it takes to complete the entire journey is 4 seconds. Draw the diagram on a piece of paper, and you will see the end point is 8 meters west of the starting point, so this value is the displacement. The total time it takes is 4 seconds, so the average speed is 8 meters west / 4 seconds = 2 meters/second west.
Method 2 of 2: Calculating the Average Velocity of Fixed Acceleration

Step 1. Consider the initial velocity and constant acceleration
Let's say our problem is "A bicycle is moving to the right with a speed of 5 m/s, with a constant acceleration of 2 m/s2. If this bicycle moves for 5 seconds, what is its average speed?"
If the unit "meter/second2" to confuse you, write it as "meters/second/second" or "meters per second per second." An acceleration of 2 meters/second/second means the speed is increasing by 2 meters per second every second.

Step 2. Use acceleration to find the final velocity
Acceleration, denoted by the notation a, is the rate of change of velocity (or rate). Speed increases at a constant rate of increase. You can draw a table using acceleration to find the speed at different times throughout the bicycle journey. We need to create this table to find the end point of the problem (at t = 5 seconds), but we will create a longer table to make it easier for you to grasp this concept:
- At the starting point (time t = 0 seconds), the bicycle is moving at a speed of 5 meters/s.
- After 1 second (t = 1), the bicycle is moving at a speed of 5 meters/second + at = 5 meters/second + (2 meters/second2)(1 second) = 7 meters/second.
- At t = 2, the bicycle is moving to the right at a speed of 5+(2)(2) = 9 meters/sec.
- At t = 3, the bicycle is moving to the right at a speed of 5+(2)(3) = 11 meters/sec.
- At t = 4, the bicycle is moving to the right at a speed of 5+(2)(4) = 13 meters/sec.
- At t = 5, the bicycle is moving to the right with a speed of 5+(2)(5) = 15 meters/second.

Step 3. Use this formula to find the average speed
If and "only" if the acceleration is constant, the average velocity will be equal to the average value of the sum of the final and initial velocities. (vf +vi)/2. For our example problem above, the initial speed of the bicycle is vi 5 meters/second. After we calculate, the final velocity is vf 15 meters/second. Adding these two values together, we get (15 meters/second + 5 meters/second) / 2 = (20 meters/second) / 2 = 10 meters/second right direction.
- Remember to include the direction, in this case "right."
- This term can be written as v0 (velocity at time 0, or initial velocity) and v (final velocity).

Step 4. Understand the average velocity formula intuitively
To find the average velocity, we can use the velocity at any point and find the average for all of them. (This is the definition of an average.) Since this requires calculus or infinite time, understand this formula more intuitively. Instead of taking each time, calculate the average velocity of the two time points and see the results. One point in time is near the start of the journey, where the bike is going slowly, and another point is near the end point when the bike is going fast.

Step 5. Test intuitive theory
Use the table above to determine the speed at different points in time. Some pairs that meet our criteria are (t=0, t=5), (t=1, t=4), or (t=2, t=3). You can test this this formula with t values other than integers too, if you want.
Whichever pair of points you choose, the average velocity at that time will always be the same. For example, ((5+15)/2), ((7+13)/2), or ((9+11)/2) all equal 10 meters/sec to the right

Step 6. Complete the intuitive explanation
If we use this method with a list of each time taken, we will continue to calculate the average of the first half of the trip and the second half of the trip. The time it takes to cover each half is the same, so no speed is lost when we finish counting.
- Since either pair will give the same result, the average of these speeds will also be the same in value. In our example, the speed of the whole is "10 meters/sec rightward" will still be 10 meters/sec rightward.
- We can find this value by calculating the average of any pair, for example the initial and final velocities. In our example, these speeds are reached at t=0 and t=5, and can be calculated using the formula above: (5+15)/2 = 10 meters/sec to the right.

Step 7. Understand this formula mathematically
If you're more comfortable with proofs written as formulas, you can start with a formula to calculate the distance traveled assuming constant acceleration, and derive the formula from there:
- s = vit + at2. (Technically s and t, or change in position and change in time, but you'd be understood as well if you wrote s and t.)
- Average speed vav defined as s/t, so enter the formula in the form s/t.
- vav = s/t = vi + at
- Acceleration x time is equal to the change in total velocity, or vf - vi. So we can replace "at" in the formula, and get:
- vav = vi + (vf - vi).
- Simplify: vav = vi + vf - vi = vi + vf = (vf +vi)/2.
Tips
- Velocity is different from speed because velocity is a vector quantity whereas speed is a scalar quantity. Vector quantities involve both direction and magnitude, while scalar quantities involve only magnitude.
- If the object is moving in one dimension, such as left-right, you can use a positive number to represent one direction (such as right) and a negative number to represent another direction (left). Write this notation at the top of your page so that it is clear to people reading your work.






