The weighted average, also known as the weighted mean, is slightly more complicated than the ordinary arithmetic mean. As the name implies, a weighted average is when the numbers being worked out have values, or weights that are related to each other. For example, we recommend that you use a weighted average if you want to calculate a total grade in a course that has a weighted percentage for each assignment. The procedure used will be slightly different, depending on whether the total weight is 1 (or 100%) or not.
Step
Method 1 of 2: Calculating the Weighted Average If the Total Weight Is 1
Step 1. Collect the numbers you want to average
You need to start by listing the numbers you want to work with. For example, if you want to calculate the weighted average of grades in a class, first write them down in a list.
For example, say in a course your total score is 82 for quizzes, 90 for exams, and 76 for paper assignments
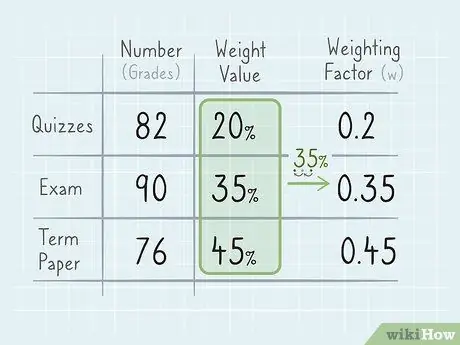
Step 2. Determine the weighted value of each number
When you have all the numbers ready, you will need to know the weight of each as part of the final average. For example, in related courses, quizzes weigh 20% of the total score, while exams weigh 35% and papers weigh 45%. In this case, the total number of weights is 1 (or 100%).
To be able to use percentages in calculations, you need to convert them to decimal numbers. The result is called the "weighting factor"
Tip:
Percentages can be converted to decimal numbers easily! Just slide the decimal point two digits to the left of the number. For example, 75% turns into 0.75.
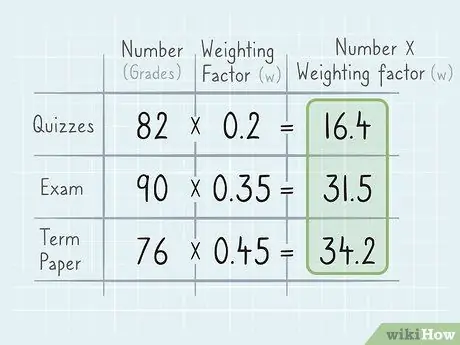
Step 3. Multiply each number by its weighting factor (w)
Once you have all the numbers, match each number (x) with its weighting factor (w). You'll multiply each set of numbers and weights, then add up all the results to find the average.
For example, if your total quiz score is 82 and the quiz weight is 20%, multiply 82 x 0.2. In this case, x=82 and w=0, 2
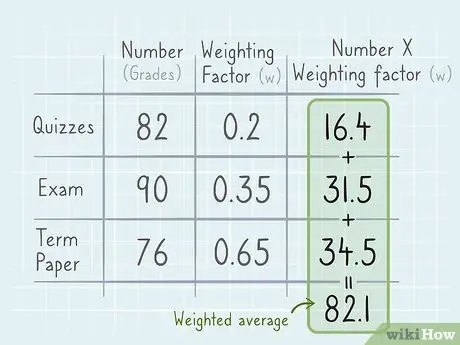
Step 4. Add up all the products to find the weighted average
The basic formula for a weighted average whose total weight is 1 is x1(w1) + x2(w2) + x3(w3), and so on, where x is each number in the set and w is the corresponding weighting factor. To find the weighted average, simply multiply each value by its weighting factor and add up all the results. As an example:
The weighted average scores for quizzes, exams, and papers are as follows: 82(0, 2) + 90(0, 35) + 76(0, 45) = 16, 4 + 31, 5 + 34, 2 = 82, 1. That is, you have a score of 82.1% in the related subject
Method 2 of 2: Calculating Weighted Average If Total Weight Is Not Equal 1
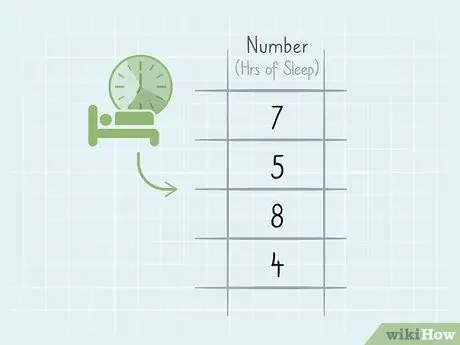
Step 1. Write down the numbers you want to average
When you calculate a weighted average, the total weight doesn't always equal 1 (or 100%). Either way, start collecting data to be able to calculate the average.
For example, maybe you want to calculate the average sleep time each night over a 15-week span. Every day your sleep time can vary, for example 5, 8, 4, or 7 hours per night
Step 2. Find the weighting factor for each number
Once all the numbers have been collected, find the total weight associated with each number. For example, say over a 15-week span, you sleep more on some nights, and less on others. In this case, the week can be used as a “weight” because it represents the average number of nights you sleep during the week. Thus, the weighing factor is the number of weeks associated with each length of sleep. For example, here are the weighing factors and their associated numbers in order of most weeks:
- 9 weeks when you average 7 hours of sleep per night.
- 3 weeks when you sleep 5 per night.
- 2 weeks when you sleep 8 hours per night.
- 1 week when you sleep 4 hours per night.
- The number of weeks that each number corresponds to is your weighing factor. In this case, you get at most 7 hours of sleep per night for most weeks, and other weeks you sleep more or less.
Step 3. Calculate the total weighing factor
To be able to determine a weighted average, you need to add up all the weighing factors to get the total. In this example, we've seen that the total weighting factor is 15 because you're observing sleep patterns over a 15-week span.
The total number of weeks is as follows: 3 weeks + 2 weeks + 1 week + 9 weeks = 15 weeks
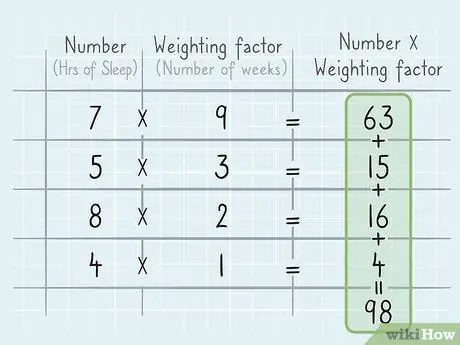
Step 4. Multiply each number by its weighting factor and add up the results
Next, you need to multiply each number in the data by its respective weighting factor, just like when calculating data where the total weight is 1 or 100%. If so, add up the results. For example, if you're calculating hours of sleep over a 15-week span, multiply the average hours of sleep by the corresponding number of weeks. You will get:
5 hours per night (3 weeks) + 8 hours per night (2 weeks) + 4 hours per night (1 week) + 7 hours per night (9 weeks) = 5(3) + 8(2) + 4(1) + 7(9) = 15 + 16 + 4 + 63 = 98
Step 5. Divide the result of the above calculation by the sum of the weights to find the average
After multiplying the number by the corresponding weighting factor, then adding up the results, divide by the number of weights to obtain a weighted average. As an example:
