The geometric mean is another way of finding the average value of a set of numbers, which is done by multiplying the values before taking the roots, instead of adding up the values and dividing them as in an arithmetic mean. Geometric averages can be used to calculate the average rate of return in financial analysis or indicate the growth rate of something over a period of time. To find the geometric mean, multiply all the values before rooting by, which is the total number of numbers in the set. You can also use the logarithm function in your calculator to find the geometric mean, if you prefer.
Step
Method 1 of 2: Finding the Geometric Average of a Set of Values
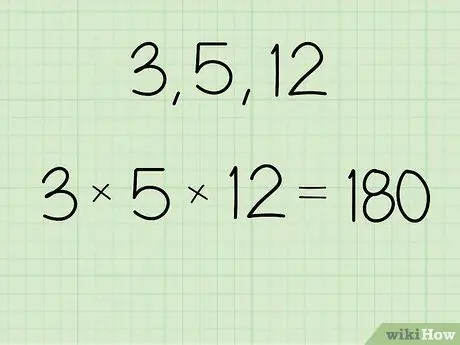
Step 1. Multiply the value for which you want to find the geometric mean
You can use a calculator or calculate manually to get the result. Write down the results so you don't forget.
- For example, if the set of numbers is 3, 5, and 12, calculate: (3 x 5 x 12) = 180.
- For another example, if you want to find the geometric mean of the set of numbers 2 and 18, write: (2 x 18) = 36.
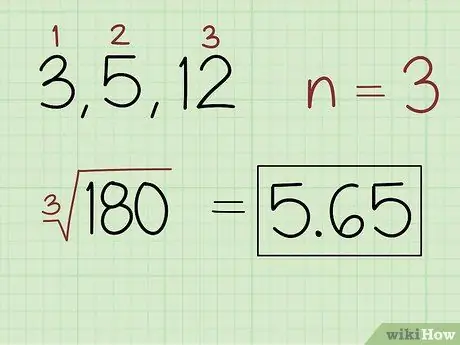
Step 2. Find the nth root of the product, where n is the number of values in the set
Count the number of numbers in the set to get the value. Use the values to specify the root that needs to be used in the product. For example, use the square root if the set contains 2 numbers, the cubic root if the set contains 3 numbers, and so on. Use a calculator to solve the equation and write down the answer.
- For example, for a set of numbers 3, 5, and 12, write: (180) 5, 65.
- In the second example with the set containing 2 and 18, write: (36) = 6.
Variation:
You can also write the root as the exponent of 1/, if it's easier to write on a calculator. For example, for the set of numbers 3, 5, and 12, write (180)1/3 instead of (180).
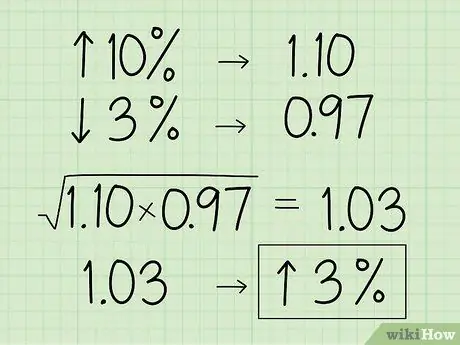
Step 3. Convert the percentage to its decimal multiplier equivalent
If the set of numbers is written as an increase or decrease in percentage, try not to use the percentage value in the geometric mean because the results will not be accurate. If the percentage increases, move the decimal point two digits to the left and add 1. If the percentage decreases, move the decimal point 2 digits to the left and subtract from 1.
- For example, say you want to find the geometric mean of object values that increases by 10%, then decreases by 3%.
- Convert 10% to a decimal number and add 1 to get 1, 10.
- Then, convert 3% to a decimal number and subtract 1 to get 0.97.
- Use both decimal places to find the geometric mean: (1, 10 x 0.97) 1.03.
- Convert the number back to a percentage by shifting the decimal point by 2 digits to the right and subtracting 1 to get a 3% increase in value.
Method 2 of 2: Calculating the Geometric Average Using Logarithms
Step 1. Add up the logarithmic values for each number in the set
The LOG function in the calculator takes the base 10 of a number and determines how much you need to multiply by 10 so that it equals the number. Look for the LOG function on the calculator, which is usually on the left side of the button. Click the LOG button and enter the first number in the set. Type “+” before entering LOG for the second number. Continue to separate the LOG function for each number with a plus symbol before obtaining the sum.
- For example, for sets 7, 9, and 12, type log(7) + log(9) + log(12), then press “=” on the calculator. If the function has been calculated, the number will be around 2.878521796.
- You can also calculate each logarithm separately before adding them all together.
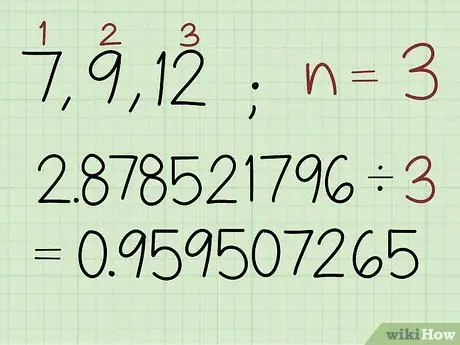
Step 2. Divide the sum of the logarithmic values by the number of numbers in the set
Count the number of values in the set and divide the previously obtained number by that number. The result is the logarithm of the geometric mean.
In this example, there are 3 numbers in the set so type: 2, 878521796 / 3 0, 959507265
Step 3. Find the antilog of the quotient to determine the geometric mean
The antilog function is the inverse of the LOG function on the calculator and converts the value back to base 10. Look for the symbol “10x” on the calculator, which is usually a secondary function of the LOG button. Press the “2nd” button on the top left corner of the calculator followed by the LOG button to activate antilog. Type in the quotient found in the last step before solving the equation.
For this example, the calculator will display: 10(0, 959507265) ≈ 9, 11.
Tips
- You cannot find the geometric mean of negative numbers.
- All sets that have 0 will have a geometric mean of 0.
