The reciprocal or reciprocal is very useful in all kinds of algebraic equations. For example, when you divide one fraction by another, you multiply the first fraction by the reciprocal of the second. You also need to use the inverse when looking for the equation of a line.
Step
Method 1 of 3: Finding the Inverse of a Fraction or Integer
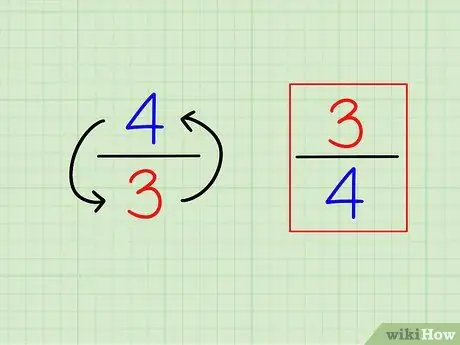
Step 1. Find the reciprocal of the fraction by inverting it
The definition of “reciprocal” or the opposite is very easy. To find the reciprocal of any integer, simply calculate "1 (that number)". For fractions, the reciprocal is a different fraction, that is, the numbers are "inverted" (inverse).
- For example, the opposite of 3/4 is 4/3.
- Any number when multiplied by its reciprocal returns 1.
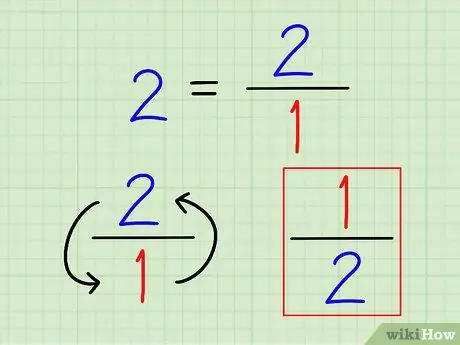
Step 2. Write the reciprocal of the whole number as a fraction
Again, the reciprocal of a number is always 1 (that number). For whole numbers, write them as fractions. There's no point in calculating that number to a decimal.
For example, the reciprocal of 2 is 1 2 = 1/2.
Method 2 of 3: Finding the Inverse of a Mixed Fraction
Step 1. Identify mixed numbers
Mixed fractions consist of whole numbers and fractions, such as 24/5. There are two steps to finding the reciprocal of a mixed number as described below.
Step 2. Convert mixed numbers to improper fractions
Remember that 1 can always be written as (number)/(same number), and fractions with the same denominator (bottom number) can be added together. Here is an example using 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
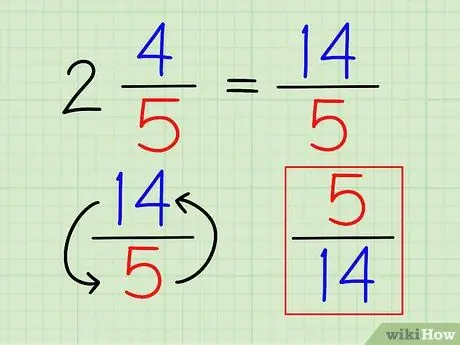
Step 3. Flip the fraction over
Once the number is written completely as a fraction, you can find its reciprocal just as you would any other fraction, by reversing the fraction.
In the example above, the reciprocal of 14/5 is 5/14.
Method 3 of 3: Finding the Opposite of a Decimal
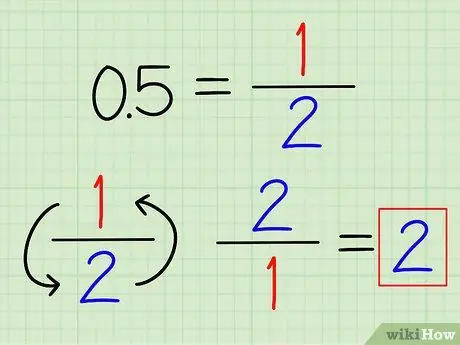
Step 1. Convert decimals to fractions if possible
You may recognize some frequently used decimal numbers, which can be easily converted to fractions. For example, 0.5 = 1/2 and 0.25 = 1/4. Once the decimal has been converted to a fraction, simply flip the fraction over to find its reciprocal.
For example, the reciprocal of 0.5 is 2/1 = 2.
Step 2. Write a division problem
If you can't convert it to a fraction, calculate the reciprocal of the number in the form of a division problem: 1 (decimal). You can use a calculator to solve it or proceed to the next step to solve it manually.
For example, you can find the reciprocal of 0.4 by calculating 1 0.4
Step 3. Change the division problem to use whole numbers
The first step to dividing a decimal is to move the decimal point until all the numbers are whole numbers. As long as you move the decimal point of both numbers by the same number of steps, you'll get the right answer.
For example, you can use 1 0, 4 and rewrite it as 10 4. In this case, you move all the decimal places one step to the right, the same as multiplying each number by ten
Step 4. Solve the problem using long division
Use the long division method to calculate the reciprocal. If you count 10 4, you will get the answer 2, 5 which is the reciprocal of 0, 4.
Tips
- The negative reciprocal of a number is the same as the regular reciprocal, in that it is multiplied by negative one. For example, the negative reciprocal of 3/4 is -4/3.
- The reciprocal or reciprocal is often referred to as the "multiplication inverse".
- The number 1 is the opposite of itself because 1 1 = 1.
- The number 0 has no reciprocal because 0 is undefined.
