- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Whenever you take a measurement while collecting data, you may assume that there is a true value within the range of the measurement you are taking. To calculate the uncertainty of your measurement, you need to find the best approximation of your measurement and take the results into account when you add or subtract measurements with their uncertainties. If you want to know how to calculate uncertainty, just follow these steps.
Step
Method 1 of 3: Learning the Basics

Step 1. Write down the uncertainty in the appropriate form
Let's say you measure a stick that is about 4.2 cm long, with a millimeter more or less. This means that you know the length of the stick is about 4.2 cm, but the actual length can be shorter or longer than that measurement, with an error of one millimeter.
Write down the uncertainty like this: 4.2 cm ± 0.1 cm. You can also write it as 4.2 cm ± 1 mm, because 0.1 cm = 1 mm

Step 2. Always round your experimental measurements to the same decimal place as the uncertainty
Measurements involving the calculation of uncertainty are usually rounded to one or two significant digits. The most important thing is that you should round your experimental measurements to the same decimal place as the uncertainty to make your measurements consistent.
- If your experimental measurement is 60 cm, then your calculation of uncertainty should also be rounded to an integer. For example, the uncertainty for this measurement might be 60 cm ± 2 cm, but not 60 cm ± 2.2 cm.
- If your experimental measurement is 3.4 cm, then your calculation of uncertainty should also be rounded to 0.1 cm. For example, the uncertainty for this measurement might be 3.4 cm ± 0.1 cm, but not 3.4 cm ± 1 cm.

Step 3. Calculate the uncertainty of one measurement
Suppose you measure the diameter of a round ball with a ruler. This measurement is tricky because it can be difficult to tell exactly where the outside of the ball is with a ruler because it is curved, not straight. Suppose a ruler can measure to an accuracy of 0.1 cm - this does not mean that you can measure the diameter to this level of accuracy.
- Study the sides of the ball and the ruler to get an understanding of how accurately you can measure the diameter. In a normal ruler, the 0.5 cm mark appears clearly - but suppose you can zoom out. If you can reduce it to about 0.3 of the accurate measurement, then your uncertainty is 0.3 cm.
- Now, measure the diameter of the ball. Suppose you get a measurement of about 7.6 cm. Just write down the approximate measurement with the uncertainty. The diameter of the ball is 7.6 cm ± 0.3 cm.
Step 4. Calculate the uncertainty of one measurement of various objects
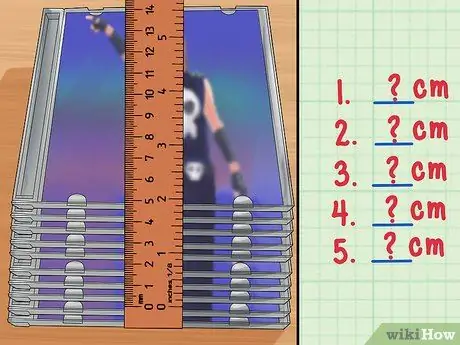
Suppose you measure a stack of 10 CD trays that are the same length. Suppose you want to find the thickness measurement for only one CD holder. This measurement will be so small that your percentage of uncertainty will be quite high. However, when you measure 10 stacked CD bins, you can divide the result and its uncertainty by the number of CD bins to find the thickness of a single CD holder.
- Suppose you can't get a measurement accuracy of less than 0.2 cm by using a ruler. So, your uncertainty is ±0.2 cm.
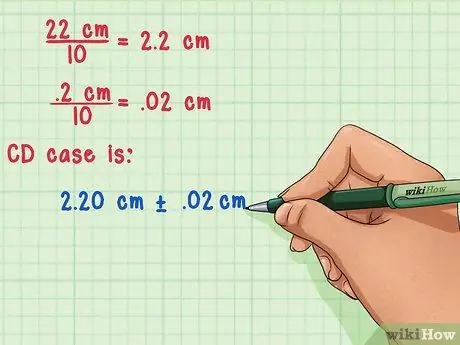
- Suppose you measure that all stacked CD holders are 22 cm thick.
- Now just divide the measurement and its uncertainty by 10, the number of CD holders. 22 cm/10 = 2.2 cm and 0.2/10 = 0.02 cm. This means that the thickness of one place CD is 2.20 cm ± 0.02 cm.
Step 5. Take your measurements many times
To increase the certainty of your measurements, whether you are measuring the length of an object or the time it takes for an object to travel a certain distance, you will increase your chances of getting an accurate measurement if you measure several times. Finding the average of some of your measurements will give you a more accurate picture of the measurements when calculating uncertainty.
Method 2 of 3: Calculating the Uncertainty of Multiple Measurements
Step 1. Take several measurements
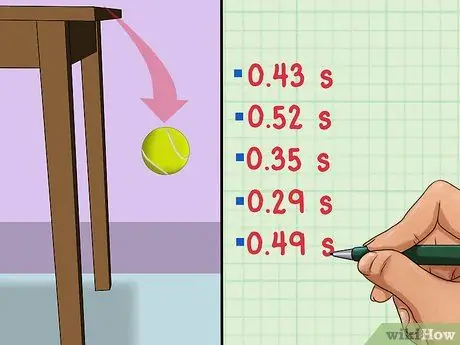
Suppose you want to calculate the time it takes a ball to fall to the floor from the height of a table. For best results, you should measure the ball falling off the table at least a few times - say five times. Then, you have to find the average of the five measurements and then add or subtract the standard deviation from that number to get the best result.
Suppose you measure five times: 0.43 s; 0.52 s; 0.35 s; 0.29 s; and 0.49 s
Step 2. Find the average of the measurements
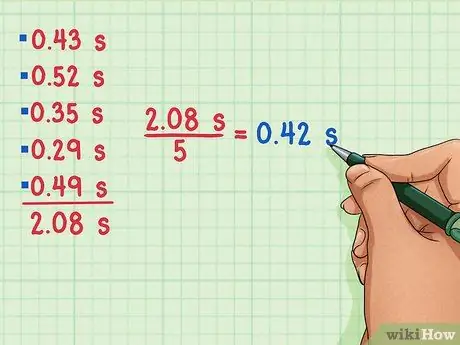
Now, find the average by adding up the five different measurements and dividing the result by 5, the number of measurements. 0.43 s + 0.52 s + 0.35 s + 0.29 s + 0.49 s = 2.08 s. Now, divide 2.08 by 5. 2.08/5 = 0.42 s. The mean time is 0.42 s.

Step 3. Look for variations in this measurement
To do this, first, find the difference between the five measurements and their average. To do so, simply subtract your measurement by 0.42 s. Here are the five differences:
-
0.43 s - 0.42 s = 0.01 s
- 0.52 s - 0.42 s = 0.1 s
- 0.35 s - 0.42 s = -0.07 s
- 0.29 s - 0.42 s = -0, 13 s
- 0.49 s - 0.42 s = 0.07 s
- Now, add up the square of the difference: (0.01 s)2 + (0, 1s)2 + (-0.07 s)2 + (-0, 13s)2 + (0.07 s)2 = 0.037 s.
- Find the average of this sum of squares by dividing the result by 5. 0.037 s/5 = 0.0074 s.
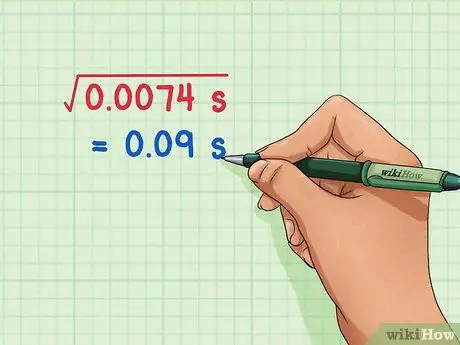
Step 4. Find the standard deviation
To find the standard deviation, just find the square root of the variation. The square root of 0.0074 s = 0.09 s, so the standard deviation is 0.09 s.

Step 5. Write down the final measurement
To do this, simply write down the average of the measurements by adding and subtracting the standard deviation. Since the mean of the measurements is 0.42 s and the standard deviation is 0.09 s, the final measurement is 0.42 s ± 0.09 s.
Method 3 of 3: Performing Arithmetic Operations with Uncertain Measurements

Step 1. Add up the uncertain measurements
To sum uncertain measurements, simply add up the measurements and their uncertainties:
- (5 cm ± 0.2 cm) + (3 cm ± 0.1 cm) =
- (5 cm + 3 cm) ± (0.2 cm + 0.1 cm) =
- 8 cm ± 0.3 cm
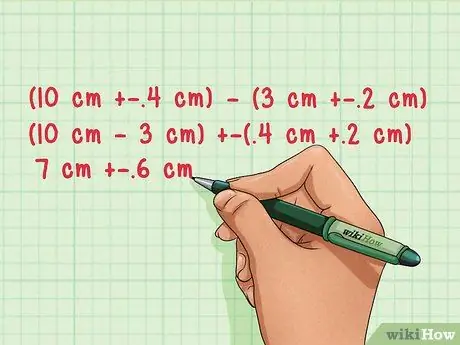
Step 2. Subtract the uncertain measurements
To subtract an uncertain measurement, simply subtract the measurement while still adding the uncertainty:
- (10 cm ± 0.4 cm) - (3 cm ± 0.2 cm) =
- (10 cm - 3 cm) ± (0.4 cm + 0.2 cm) =
- 7 cm ± 0.6 cm

Step 3. Multiply the uncertain measurements
To multiply uncertain measurements, simply multiply the measurements while adding up the RELATIVE uncertainties (in percentage): Calculating the uncertainty by multiplication does not use absolute values (as in addition and subtraction), but uses relative values. You get the relative uncertainty by dividing the absolute uncertainty by the measured value and multiplying by 100 to get a percentage. For example:
-
(6 cm ± 0.2 cm) = (0, 2/6) x 100 and add the % sign. To be 3, 3%.
Therefore:
- (6 cm ± 0.2 cm) x (4 cm ± 0.3 cm) = (6 cm ± 3.3%) x (4 cm ± 7.5%)
- (6 cm x 4 cm) ± (3, 3 + 7, 5) =
- 24 cm ± 10.8% = 24 cm ± 2.6 cm

Step 4. Divide the uncertain measurements
To divide uncertain measurements, simply divide the measurements while adding up the RELATIVE uncertainties: The process is the same as multiplication!
- (10 cm ± 0.6 cm) (5 cm ± 0.2 cm) = (10 cm ± 6%) (5 cm ± 4%)
- (10 cm 5 cm) ± (6% + 4%) =
- 2 cm ± 10% = 2 cm ± 0.2 cm
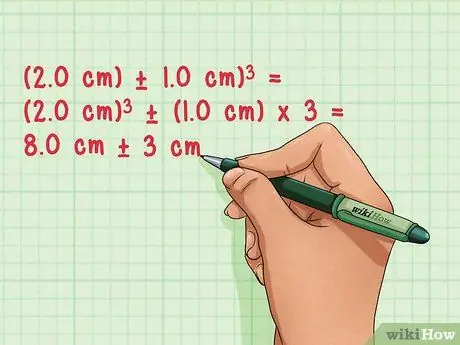
Step 5. The power of the measurement is uncertain
To raise an uncertain measurement, simply raise the measurement to the power, and then multiply the uncertainty by that power:
- (2.0 cm ± 1.0 cm)3 =
- (2.0 cm)3 ± (1.0 cm) x 3 =
- 8.0 cm ± 3 cm
Tips
You can report results and standard uncertainties as a whole, or for individual results in a data set. As a general rule, data drawn from multiple measurements is less accurate than data drawn directly from each measurement
Warning
- Uncertainty, in the manner described here, can only be used for cases of normal distribution (Gauss, bell curve). Other distributions have different meanings in describing uncertainty.
- Good science never talks about facts or truth. While it is likely that an accurate measurement is within your uncertainty range, there is no guarantee that the measurement is within that range. Scientific measurement basically accepts the possibility of error.






