- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
There are various ways to do the division. You can divide decimals, fractions, or even exponents, and use long or short division. If you want to know the different ways of dividing numbers, follow the steps below.
Step
Method 1 of 5: Performing Long Series Division

Step 1. Write down the questions
To do long division, place the denominator (the number that will divide) outside the divisor bar, and the numerator (the number to be divided) inside the divisor bar.
For example: 136÷3

Step 2. Divide the first digit of the numerator by the denominator (if possible)
In this example, 1 is not divisible by 3 so put a 0 above the divisor bar and move on to the next step. Subtract 1 by 0 and put the result under the number 1.

Step 3. Divide the number of the remainder of the first digit of the numerator and the second digit of the numerator by the denominator
Since 1 cannot be divided by 3, the number 1 is still used. You need to subtract 3. Now, divide 13 by 3. Since 3 x 4 = 12, put the number 4 above the divisor bar (to the right of 0), then subtract 13 by 12 and write the result below it.

Step 4. Divide the remaining numbers by the denominator
Lower the number 6 to the right of 1, to get 16. Now, divide 16 by 3. Since 3 x 5 = 15, write the number 5 to the right of the number 4, and subtract 16 by 15 and write the result (16-15= 1) below it.

Step 5. Write the remainder next to the quotient
Your final answer is 45 with 1 remaining, or 45 R1.
Method 2 of 5: Performing Short Divisions

Step 1. Write down the questions
Write the denominator (the number to divide) outside the divisor bar, and the numerator (the number to be divided) inside the divisor bar. Note that in short division, the denominator cannot be more than one digit.
For example, 518 4

Step 2. Divide the first digit of the numerator by the denominator
5 4 = 1 R1. Place the quotient (1) above the long divider bar. Write the remainder above the first digit of the numerator. Place a small 1 over 5 to remind you that you have 1 left when you divide 5 by 4. The 518 should now look like this: 5118

Step 3. Divide the number formed from the remainder and the second digit of the numerator by the denominator
The next number is 11 which is obtained from the residual value (1) and the second digit of the numerator (1). 11 4 = 2 R 3 because 4 x 2 = 8 with a remainder of 3. Write the residual value above the second digit of the numerator. Put 3 over 1. The initial numerator (518) now looks like this: 51138

Step 4. Divide the remaining numbers by the denominator
The remaining number is 38; the number 3 comes from the remainder of the previous stage, and 8 is the last digit of the numerator. Calculate 38 4 = 9 R2. Since 4 x 9 = 36, write "R2" above the division bar because 38 - 36 = 2.

Step 5. Write down the final answer
The final result and the quotient are above the divisor bar. The answer is 518 4 = 129 R2.
Method 3 of 5: Divide Fractions

Step 1. Write down the questions
To divide a fraction, simply write down the first fraction followed by the divide symbol and then the second fraction.
For example: 3/4 5/8

Step 2. Reverse the numerator and denominator of the second fraction
The second fraction is now reciprocal.
Example: 3/4 8/5

Step 3. Change the divide symbol to the times symbol
To divide a fraction, you multiply the first fraction by the reciprocal of the second.
Example: 3/4 x 8/5
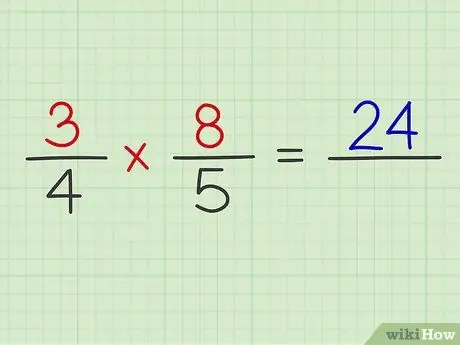
Step 4. Multiply the numerator of both fractions
Just do it like multiplying two regular fractions.
Example: 3 x 8 = 24
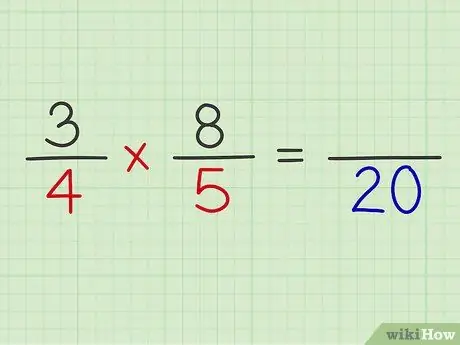
Step 5. Multiply the denominators of both fractions
Complete the calculation by multiplying the two fractions.
Example: 4 x 5 = 20
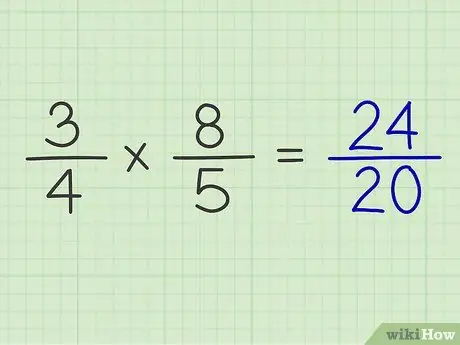
Step 6. Put the product of the numerator above the product of the denominator
After multiplying the numerator and denominator of the two fractions, you can get the result of calculating both fractions.
Example: 3/4 x 8/5 = 24/20

Step 7. Simplify fractions
To find the Greatest Common Factor, or the largest number that divides the numerator and denominator equally. In this case the greatest common factor of 24 and 20 is 4. To prove it, write down all the factors in both the numerator and denominator, and circle the number of the greatest common factor of the two.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- Since 4 is the greatest common factor of 24 and 20, just divide the two numbers by 4 to simplify the fraction.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

Step 8. Rewrite the fraction as a mixed number (optional)
The trick, just divide the numerator by the denominator, and write the result as a whole number. After that write the remainder of the division as a new numerator, and the denominator of the fraction does not change. Since 6 divided by 5 results in 1 with a remainder of 1, write the whole number 1, followed by the new numerator 1, then the denominator 5 to get a mixed number 1 1/5.
Example: 6/5 = 1 1/5
Method 4 of 5: Divide Exponent

Step 1. Make sure the exponents/powers have the same base number
You can only divide exponents if they have the same base number. Otherwise, you can try manipulating them until you get the same base number.
Example: x8 x5

Step 2. Subtract the exponent
You can simply subtract the first exponent by the second. Don't mind the base numbers for now.
Example: 8 - 5 = 3
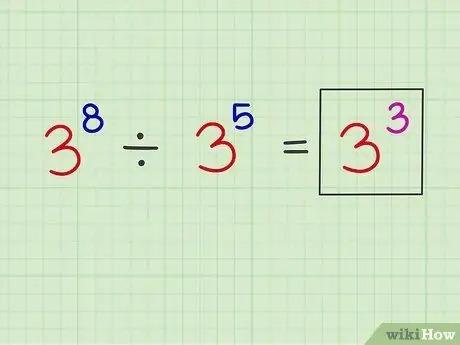
Step 3. Place the new exponent above the original base number
Now, you can write the new exponent over the original base number.
Example: x8 x5 = x3
Method 5 of 5: Dividing Decimal Numbers

Step 1. Write down the questions
Write the denominator (the number to divide) outside the divisor bar, and the numerator (the number to be divided) inside the divisor bar. In decimal division, your goal is to convert a decimal number to a whole number.
Example: 65.5.5

Step 2. Change the denominator to a whole number
Just slide the decimal point by one digit to the right to change 0.5 to 5, aka 5, 0.

Step 3. Change the numerator by shifting the decimal point by the same number of digits as the denominator
Because you move the decimal point of the numerator by one digit to the right so that it becomes a whole number, the decimal point of the denominator is also shifted by one digit to the right so that 65.5 changes to 655.
If you shift the decimal point of the numerator beyond all of its digits, it means that you need to add zeros to the digits each time the decimal point is shifted. For example, if the decimal point 7, 2 is shifted three digits to the right, the number changes to 7,200 because the two-digit blank space is filled with zeros

Step 4. Place the decimal point on the long division bar just above the decimal point in the numerator
Since you're shifting the decimal point by one digit to make 0.5 a whole number, it's a good idea to place the decimal point above the division bar exactly where the decimal point is shifted, i.e. after the last 5 in 655.

Step 5. Solve the problem with simple long division
To divide 655 by 5, the steps are:
- Divide the hundreds digit of the numerator (6) by the denominator (5). The result is 1 with a remainder of 1. Write the number 1 above the divisor bar, and write 5 under the number 6 to be subtracted.
- The remainder of 1 is subtracted from the tens digit of the numerator (5) so that you now get 15. Divide 15 by 5 to get 3. Write 3 above the divisor bar, to the right of 1.
- Drop the last 5 digits. Divide 5 by 5 to get 1. Write the number 1 above the divisor bar, to the right of the number 3. There is no remainder because 5 is divisible by 5.
- The long sequential division answer is 655 5 = 131. This result is the same as the answer to questions 65.5 0.5.






