IQR is the interquartile range or the quartile root range of a data set. IQR is used in statistical analysis to help draw conclusions about a data set. IQR is used more often than range because IQR does not include the outermost data. Continue reading to learn how to find the IQR!
Step
Method 1 of 3: Understanding IQR
Step 1. Understand how to use IQR
Basically, IQR is a way of understanding the spread of a set of numbers. The root quartile range is defined as the difference between the upper quartile (25% top) and the lower quartile (25% lowest) of the data set.
Tip:
The lower quartile is usually written as Q1, and the upper quartile is written as Q3 – which technically makes the midpoint of the data to be Q2 and the highest point to be Q4.
Step 2. Understand the quartiles
To illustrate quartiles, divide the set of numbers into four equal parts. Each of these parts is a “quartile”. Suppose the data sets are: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 and 2 are the first quartile or Q1
- 3 and 4 are the second quartile or Q2
- 5 and 6 are the third quartile or Q3
- 7 and 8 are the fourth quartile or Q4
Step 3. Learn the formula
To find the difference between the upper and lower quartiles, you must subtract the 75th percentile from the 25th percentile.
The formula is written: Q3 – Q1 = IQR
Method 2 of 3: Compiling the Data Set
Step 1. Collect your data
If you study IQR in class and in tests, you may be given a set of data already prepared, for example 1, 4, 5, 7, 10. This is your data set – the numbers you will work with. However, you can build your own numbers from table questions or story problems.
Make sure each number represents the same thing:
for example, the number of eggs in each nest of a defined bird population, or the number of parking spaces located in each house in a specified block.
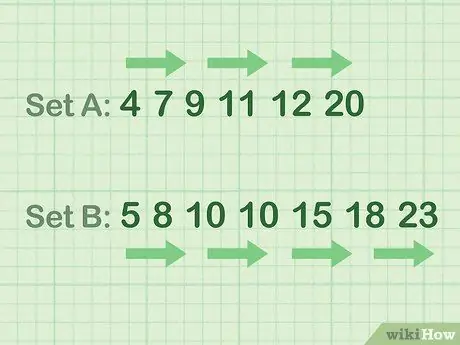
Step 2. Sort your data in ascending order
In other words: arrange the numbers from smallest to largest. Use the hints from the following examples.
- Example of even number data (Set A): 4 7 9 11 12 20
- Example of odd number data (Set B): 5 8 10 10 15 18 23
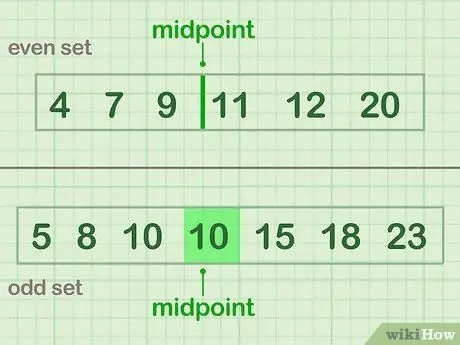
Step 3. Divide the data into two
To split in half, find the midpoint of your data: the number or numbers that are at the very center of the data set. If you have an odd number of data, choose the number that is right in the middle. If you have an even number of data, the midpoint is between the two most middle numbers.
- An even example (Set A) which has a midpoint between 9 and 11: 4 7 9 | 11 12 20
- An odd example (Set B) which has a midpoint of value (10): 5 8 10 (10) 15 18 23
Method 3 of 3: Calculating IQR
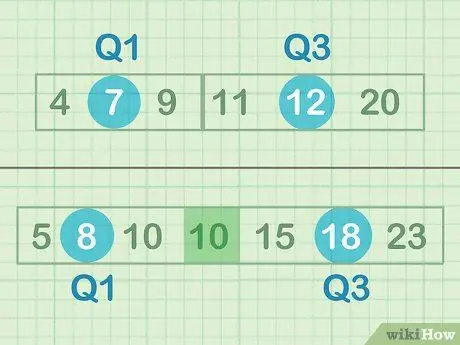
Step 1. Find the median of your lower and upper half of the data
The median is the "middle point" or number that is in the middle of a set of numbers. In this case, you are not looking for the midpoint of all the numbers, but are looking for the relative midpoint of the upper and lower data subsets. If you have an odd number of data, don't include the middle number – for example, in Set B, you don't need to include a single 10.
-
Even example (set A):
- Median of the lower half of the data = 7 (Q1)
- The median of the upper half of the data = 12 (Q3)
-
Odd example (set B):
- Median of the lower half of the data = 8 (Q1)
- The median of the upper half of the data = 18 (Q3)
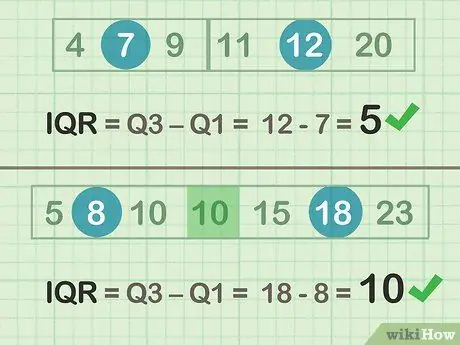
Step 2. Subtract Q3-Q1 to determine the IQR
Now you know how many numbers fall between the 25th and 75th percentiles. You can use this number to understand the spread of a data. For example, if a test has a maximum score of 100, and the IQR of the score is 5, you can assume that most people taking the test will have almost the same understanding because the range of highs and lows is not very large. However, if the IQR of a test score is 30, you may begin to wonder why some people score so high and others score so low.
- Even example (set A): 12 -7 = 5
- Odd example (set B): 18 – 8 = 10
Tips
It's important to learn to do this on your own. However, there are several online IQR calculators that you can use to check your work. Don't rely too much on calculator apps if you learn this in class! If you're asked to look up the IQR in a test, you'll need to know how to find it manually
Related WikiHow
- How to Detect Outliers
- How to Calculate the Range of a Data Set
- How to Make a Box and Tent Diagram
