- Author Jason Gerald [email protected].
- Public 2024-01-19 22:11.
- Last modified 2025-06-01 06:05.
In statistics, an outlier or “outlier” is a datum that deviates very far from any other datum within a sample or set of datums (the set of datums is called data). Oftentimes, an outlier in a datum set can serve as a warning to the statistician of an abnormality or experimental error in the measurements taken, which could lead the statistician to remove the outlier from the datum set. If the statistician removes the outliers from the datum set, the conclusions drawn from the study can be very different. Therefore, knowing how to calculate and analyze outliers is very important to ensure the correct understanding of a statistical datum set.
Step

Step 1. Learn how to identify potentially outlier datums
Before we decide whether to remove outlier datums from the datum set or not, of course we must identify which datums have the potential to become outliers. In general, an outlier is a datum that deviates very far from the other datums in one datum set-in other words, an outlier is “outside” of the other datums. It is usually easy to detect outliers in a data table or (in particular) a graph. If one set of datums is described visually with a graph, the outlier datum will appear to be "very far" from the other datums. If, for example, most of the datums in a datum set form a straight line, the outlier datum will not reasonably be interpreted as forming that line.
Let's look at a set of datums that represent the temperatures of 12 different objects in a room. If 11 objects have a temperature of about 70 Fahrenheit (21 degrees Celsius), but the 12th object, an oven, has a temperature of 300 Fahrenheit (150 degrees Celsius), it can be seen immediately that the oven temperature is very likely to be an outlier

Step 2. Arrange the datums in a set of datums from lowest to highest
The first step to calculating outliers in a datum set is to find the median (middle value) of that datum set. This task becomes very simple if the datums in a set of datums are arranged from the smallest to the largest. So, before continuing, arrange the datums in one such datum set.
Let's continue the example above. This is our set of datums representing the temperatures of several objects in a room: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. If we arrange the datums from lowest to highest, the order of the datums becomes: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}

Step 3. Calculate the median of the datum set
The median of a datum set is a datum where the other half of the datum is above that datum and the remaining half is below it-basically, that datum is the datum that is in the "middle" of the datum set. If the number of datums in a datum set is odd, it's very easy to find them-the median is the datum that has the same number above and below it. However, if the number of datums in the datum set is even, then, because no one datum fits in the middle, the 2 datums in the middle are averaged to find the median. It should be noted that, when calculating outliers, the median is usually assigned the variable Q2-ni because Q2 is between Q1 and Q3, the lower and upper quartile, which we will discuss later.
- Don't confuse it with a datum set where the number of datums is even-the average of 2 middle datums will often return numbers that aren't in the datum set itself-that's okay. However, if the 2 middle datums are the same number, the average, of course, will also be the same number, which is also fine.
- In this example, we have 12 datums. The 2 middle datums are the 6th and 7th datums-70 and 71 respectively. So, the median of our set of datums is the average of these 2 numbers: ((70 + 71) / 2), = 70.5.

Step 4. Calculate the lower quartile
This value, which we give the variable Q1, is the datum that represents 25 percent (or a quarter) of the datums. In other words, it is the datum that bisects the datums that are below the median. If the number of datums below the median is even, you must again average the 2 middle datums to find Q1, just as you would to find the median itself.
In our example, there are 6 datums that lie above the median, and 6 datums that lie below the median. This means that, to find the lower quartile, we will need to average the 2 datums in the middle of the 6 datums below the median. The 3rd and 4th datums of 6 datums below the median are both 70. So, the average is ((70 + 70) / 2), = 70. 70 becomes our Q1.

Step 5. Calculate the upper quartile
This value, which we give the variable Q3, is the datum on which there are 25 percent of the datums in the datum set. Finding Q3 is pretty much the same as finding Q1, except that, in this case, we are looking at the datums above the median, not below the median.
Continuing our example above, the 2 datums in the middle of the 6 datums above the median are 71 and 72. The average of these 2 datums is ((71 + 72) / 2), = 71, 5. 71, 5 being our Q3.
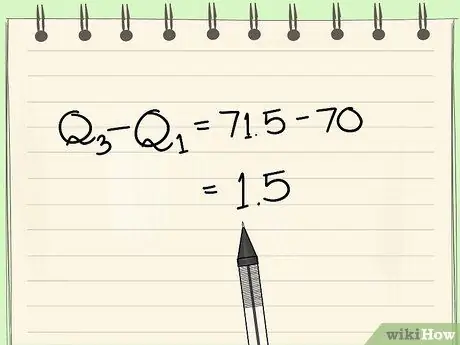
Step 6. Find the interquartile distance
Now that we have found Q1 and Q3, we need to calculate the distance between these two variables. The distance from Q1 to Q3 is found by subtracting Q1 from Q3. The values you get for interquartile distances are very important for defining the boundaries of non-outlier datums in your datum set.
- In our example, our values of Q1 and Q3 are 70 and 71, 5. To find the interquartile distance, we subtract Q3 - Q1 = 71.5 - 70 = 1, 5.
- It should be noted that this is also true even if Q1, Q3, or both are negative numbers. For example, if our Q1 value was -70, our correct interquartile distance would be 71.5 - (-70) = 141, 5.

Step 7. Find the “inner fence” in the datum set
Outliers are found by checking whether the datum falls within the number boundaries called “inner fence” and “outer fence”. A datum that falls outside the inner fence of the datum set is referred to as a “minor outlier”, while a datum that falls outside the outer fence is referred to as a “major outlier”. To find the inner fence in your datum set, first multiply the interquartile distance by 1, 5. Then, add the result by Q3 and also subtract it from Q1. The two values obtained are the inner fence boundaries of your datum set.
-
In our example, the interquartile distance is (71.5 - 70), or 1.5. Multiply 1.5 by 1.5 which results in 2.25. We add this number to Q3 and we subtract Q1 by this number to find the boundaries of the inner fence as follows:
- 71, 5 + 2, 25 = 73, 75
- 70 - 2, 25 = 67, 75
- So, the boundaries of our inner fence are 67, 75 and 73, 75.
-
In our set of datums, only the oven temperature, 300 Fahrenheit - is outside these limits and so this datum is a minor outlier. However, we still haven't calculated whether this temperature is a major outlier, so don't jump to conclusions until we've done our calculations.

Calculate Outliers Step 7Bullet2

Step 8. Find the “outer fence” in the datum set
This is done in the same way as finding the inner fence, except that the interquartile distance is multiplied by 3 instead of 1.5. The result is then added to Q3 and subtracted from Q1 to find the upper and lower bounds of the outer fence.
-
In our example, multiplying the interquartile distance by 3 gives (1, 5 x 3), or 4, 5. We find the boundaries of the outer fence in the same way as before:
- 71, 5 + 4, 5 = 76
- 70 - 4, 5 = 65, 5
- The boundaries of the outer fence are 65.5 and 76.
-
The datums that lie outside the boundary of the outer fence are referred to as major outliers. In this example, the oven temperature, 300 Fahrenheit, is clearly outside the outer fence, so this datum is "definitely" a major outlier.

Calculate Outliers Step 8Bullet2

Step 9. Use qualitative judgment to determine whether or not to “discard” the outlier datum
Using the method described above, it can be determined whether a datum is a minor datum, a major datum, or not an outlier at all. However, make no mistake-finding a datum as an outlier only marks that datum as a “candidate” to be removed from the datum set, not as a datum that “should” be discarded. The "reason" that causes an outlier datum to deviate from other datums in a datum set is very important in determining whether to discard it or not. In general, an outlier caused by an error in measurement, recording, or experimental planning, for example-can be discarded. On the other hand, outliers that are not caused by error and which indicate new information or trends that were not previously predicted are usually “not” discarded.
- Another criterion to consider is whether the outlier has a large effect on the mean of a datum set, i.e. whether the outlier confuses it or makes it appear wrong. This is very important to consider if you intend to draw conclusions from the average of your data set.
-
Let's study our example. In this example, since it seems "highly" improbable that the oven reached 300 Fahrenheit through unpredictable natural forces, we can conclude with almost certainty that the oven was accidentally left on, resulting in a datum abnormality of high temperature. Also, if we don't remove the outliers, our datum set mean is (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12 = 89.67 Fahrenheit (32 degrees Celsius), while the average if we remove the outliers is (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11 = 70.55 Fahrenheit (21 degrees Celsius).
Since these outliers were caused by human error and because it would be incorrect to say that the average room temperature reaches nearly 90 Fahrenheit (32 degrees Celsius), we are better off choosing to “throw away” our outliers

Step 10. Know the importance (sometimes) of maintaining outliers
Although some outliers should be removed from the datum set because they cause errors and/or make the results inaccurate or erroneous, some outliers should be maintained. If, for example, an outlier appears to be naturally acquired (that is, not the result of an error) and/or provides a new perspective on the phenomenon under study, the outlier should not be removed from the datum set. Scientific research is usually a very sensitive situation when it comes to outliers - incorrectly removing outliers can mean discarding information that indicates a new trend or discovery.






