- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
Adding and subtracting fractions is an important skill to have. Fractions appear in everyday life all the time, especially in math classes, from elementary to college. Follow these steps to learn how to add and subtract fractions, from equivalent fractions, unequal fractions, mixed numbers, or common fractions. If you already know one way, it's really easy to solve the other fractions!
Step
Method 1 of 4: Adding and Subtracting Fractions with the Same Denominator

Step 1. Write down your question
If the denominator of the two fractions you want to add or subtract is the same, write down the denominator once as the denominator of your answer.
In other words, 1/5 and 2/5 need not be written as 1/5 + 2/5 = ?, but can be written as (1+2)/5 = ?. The denominators are the same, so they can be written only once. The two numerators are combined
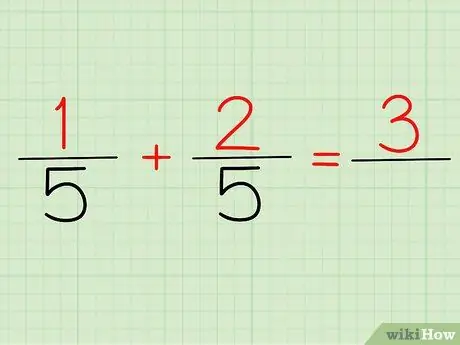
Step 2. Add up the numerators
The numerator is the number that is above any fraction. If we look at the problem above, 1/5 and 2/5, 1 and 2 are our numerators.
Whether you write it 1/5 + 2/5 or (1+2)/5, your answer will be the same: 3! Because, 1 + 2 = 3

Step 3. Leave the denominator
Since the denominators are the same, don't do anything with the denominators! Don't add, subtract, multiply, or divide. Let it be.
So, from the same example, our denominator is 5. Right! 5 is the bottom number of our fraction. We've got half the answer

Step 4. Write down your answer
Now, all you have to do is write down your numerator and denominator! If you use the example above, your answer will be 3/5.
What's your numerator? 3. Your denominator? 5. Therefore, 1/5 + 2/5 or (1+2)/5 is equal to 3/5.
Method 2 of 4: Adding and Subtracting Fractions with Different Denominators

Step 1. Find the least common denominator
That is, the smallest denominator is the same for both fractions. Suppose we have the fractions 2/3 and 3/4. What is the denominator? 3 and 4. To find the least common denominator of both fractions, you can do this in three ways:
- Write down the multiples of. Multiples of 3 are 3, 6, 9, 12, 15, 18…and so on. Multiples of 4? 4, 8, 12, 16, 20, and so on. What is the smallest number that is a multiple of the two? 12! That's the smallest common denominator.
-
Prime factorization. If you know about factors, you can do prime factorization. That is, you are looking for the numbers that make up your denominator. For number 3, the factors are 3 and 1. For number 4, the factors are 2 and 2. Then, all of you. 3 x 2 x 2 = 12. Your least common denominator!
Multiply all the numbers for the smaller number. In some problems, like this one, you can multiply both numbers - 3 x 4 = 12. However, if you have a large denominator, don't do this! You don't want to multiply 56 x 44 and go all out to get 2,464

Step 2. Multiply the denominator by the number needed to get the smallest common denominator
In other words, you want all of your denominators to be equal. In our example, we want the denominator to be 12. To change 3 to 12, you multiply 3 by 4. To change 4 to 12, you multiply 4 by 3. The same denominator will be the denominator of your final answer.
-
So 2/3 becomes 2/3 x 4 and 3/4 becomes 3/4 x 3. That is, we now have 2/12 and 3/12. But, we're not done yet!
- You'll notice that the denominators are multiplied by each other. This can be done in this situation, but not in all situations. Sometimes, instead of multiplying both denominators, you can multiply both denominators by another number to get the smaller number.
- Then in other problems, sometimes you just need to multiply one denominator to make it equal the denominator of the other fraction in the problem.

Step 3. Multiply the numerator by the same number
When you multiply the denominator by a number, you must also multiply the numerator by the same number. What we did in the last step is only part of the multiplication that has to be done.
We have 2/3x4 and 2/4x3 as the first step - then, in the second step, 2 x 4/3 x 4 and 3 x 3/4 x 3. That is, our new numbers are 8/12 and 9/12. Perfect

Step 4. Add (or subtract) the numerators to get the answer
To add 8/12 + 9/12, all you have to do is add up the numerators. Remember: just leave the denominator. The smallest common denominator you find is your final denominator.
In this example, (8+9)/12 = 17/12. To convert it to a mixed number, just subtract the denominator from the numerator and write down the remainder. In this case, 17/12 = 1 5/12
Method 3 of 4: Adding and Subtracting Mixed and Common Fractions

Step 1. Convert your mixed fractions to common fractions
A mixed number is a fraction that has both a whole number and a fraction, as in the example above (1 5/12). Meanwhile, an ordinary fraction is a fraction whose numerator (top number) is greater than the denominator (bottom number). This fraction is also seen in the previous step, which is 17/12.
For the examples in this section, we will use 13/12 and 17/8

Step 2. Find a common denominator
Do you remember the three ways to find the least common denominator? By writing multiples, using prime factorization, or multiplying the denominators.
Let's find multiples of our example, 12 and 8. What is the smallest number that both of them have in common? 24. 8, 16, 24, and 12, 24 - bingo

Step 3. Multiply your numerator and denominator to find the equivalent fraction
Both denominators must be changed to 24. How do you convert 12 to 24? Multiply by 2. 8 to 24? Multiply by three. But don't forget - you have to multiply the numerators too!
So (13 x 2)/(12 x 2) = 26/24. And (17 x 3)/(8 x 3) = 51/24. We're almost done with this

Step 4. Add or subtract your fractions
Now that you have the same denominator, you can easily add the two numerators together. Remember, just leave the denominator!
26/24 + 51/24 = 77/24. That's your sum! However, the numbers at the top were too big…

Step 5. Convert your answer back to mixed numbers
The very large number at the top of the fraction feels a bit odd - you can't tell the size of your fraction. All you have to do is subtract your denominator from the numerator repeatedly until it can't be subtracted any more and write down the remainder.
-
In this example, 77 minus 24 by 3 times. That is, 24 x 3 = 72. The remainder is 5! So what's your end result? 3 5/24.
So true!
Method 4 of 4: Add and Subtract Fractions Without Finding LCM
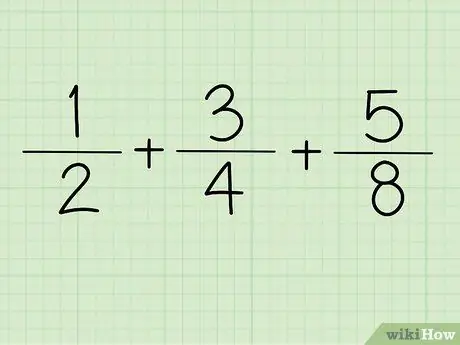
Step 1. Write down the fraction
For example + +

Step 2. Solve the numerator first
- Multiply by the other fraction's numerator.
- Multiply 1 by 4 and 8. [32]
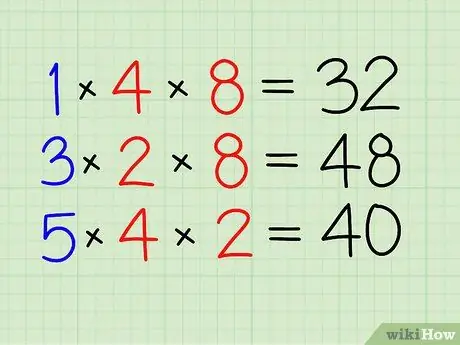
Step 3. Do the same for the other fractions
- Multiply 3 by 2 and 8. [48]
- Finally, multiply 5 by 4 and 2. [40]
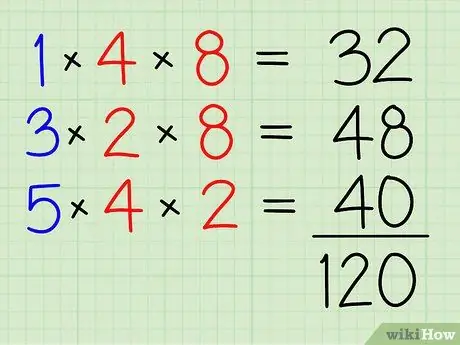
Step 4. Add them all together
32+48+40=120
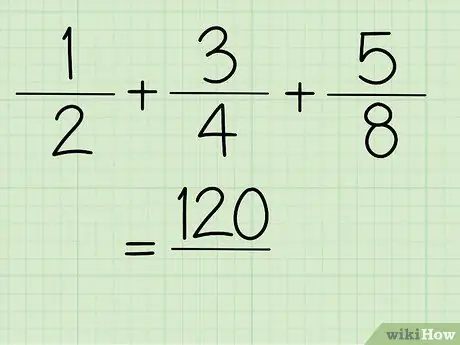
Step 5. Now, you get the numerator value

Step 6. Solve the denominator of the fraction

Step 7. Multiply all the fractions' denominators
2×4×8=64

Step 8. Now, you get the result
120/64 = 1 56/64 = 1 ⅞
Warning
- This method allows you to multiply large numbers.
- You may need a calculator to calculate this way.






