- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
To add and subtract square roots, you need to combine terms in an equation that have the same square root (radical). This means that you can add or subtract 2√3 and 4√3, but not 2√3 and 2√5. There are many problems that allow you to simplify the numbers in the square root so that like terms can be combined and square roots can be added or subtracted.
Step
Part 1 of 2: Understanding the Basics
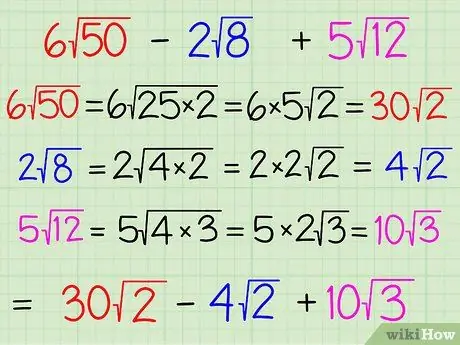
Step 1. Simplify all the terms in the square root whenever possible
To simplify the terms in the square root, try factoring so that at least one term is a perfect square, such as 25 (5 x 5) or 9 (3 x 3). If so, take the perfect square root and place it outside the square root. Thus, the remaining factors are inside the square root. For example, our problem this time is 6√50 - 2√8 + 5√12. The numbers outside the square root are called the “coefficients”, and the numbers inside the square roots are the radicands. Here's how to simplify each term:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Here, you factor "50" into "25 x 2" and then root the perfect square number "25" to "5" and put it outside the square root, leaving the number "2" inside. Then, multiply the numbers outside the square root of "5" by "6", to get "30" as the new coefficient
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Here, you factor "8" into "4 x 2" and root the perfect square number "4" to "2" and put it outside the square root, leaving the number "2" inside. After that, multiply the numbers outside the square root, i.e. “2” by “2” to get “4” as the new coefficient.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Here, you're factoring "12" into "4 x 3" and taking the root of "4" to "2" and putting it outside the square root, leaving the number "3" inside. After that, multiply the numbers outside the square root of "2" by "5", to get "10" as the new coefficient.

Step 2. Circle all the terms with the same radicand
After you simplify the radicand of the given terms, your equation looks like this 30√2 - 4√2 + 10√3. Since you're only adding or subtracting like terms, circle the terms that have the same square root, such as 30√2 and 4√2. You can think of it the same as adding and subtracting fractions, which can only be done if the denominators are the same.

Step 3. Rearrange the paired terms in the equation
If your equation problem is long enough, and there are several pairs of equal radicands, you need to circle the first pair, underline the second pair, put an asterisk in the third pair, and so on. Rearrange the equations to match their pairs so that the questions can be seen and done more easily.
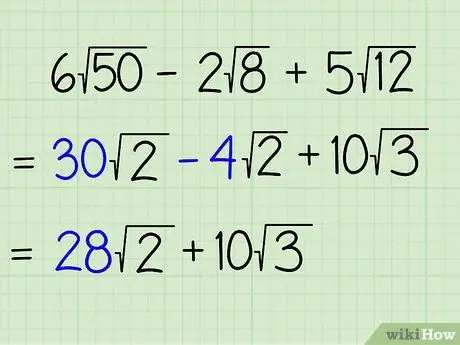
Step 4. Add or subtract the coefficients of terms that have the same radicand
Now, you just need to add or subtract the coefficients of terms that have the same radicand, leaving all the additional terms as part of the equation. Do not combine the radicands in the equation. You simply indicate the total number of types of radicands in the equation. Dissimilar tribes may be left as they are. Here's what you need to do:
- 30√2 - 4√2 + 10√3 =
- (30 - 4)√2 + 10√3 =
- 26√2 + 10√3
Part 2 of 2: Multiply Practice

Step 1. Work on Example 1
In this example, you add up the following equations: (45) + 4√5. Here's how to do it:
- Simplify (45). First, factor it into (9 x 5).
- Then, you can root the perfect square number “9” to “3” and put it outside the square root as a coefficient. Thus, (45) = 3√5.
- Now, just add the coefficients of the two terms with the same radicand to get the answer 3√5 + 4√5 = 7√5

Step 2. Work on Example 2
This sample problem is: 6√(40) - 3√(10) + 5. Here's how to solve it:
- Simplify 6√(40). First, factor "40" to get "4 x 10". Thus, your equation becomes 6√(40) = 6√(4 x 10).
- After that, take the square root of the perfect square number “4” to “2”, then multiply it by the existing coefficient. Now you get 6√(4 x 10) = (6 x 2)√10.
- Multiply the two coefficients to get 12√10.
- Now, your equation becomes 12√10 - 3√(10) + 5. Since both terms have the same radicand, you can subtract the first term from the second, and leave the third term as it is.
- The result is (12-3)√10 + 5, which can be simplified to 9√10 + 5.

Step 3. Work on Example 3
This sample problem is as follows: 9√5 -2√3 - 4√5. Here, no square root has a perfect square number factor. So, the equation cannot be simplified. The first and third terms have the same radicand so they can be combined, and the radicand is left as is. The rest, there is no longer the same radican. Thus, the problem can be simplified to 5√5 - 2√3.

Step 4. Work on Example 4
The problem is: 9 + 4 - 3√2. Here's how to do it:
- Since 9 is equal to (3 x 3), you can simplify 9 to 3.
- Since 4 is equal to (2 x 2), you can simplify 4 to 2.
- Now, you just need to add 3 + 2 to get 5.
- Since 5 and 3√2 are not the same term, nothing more can be done. The final answer is 5 - 3√2.
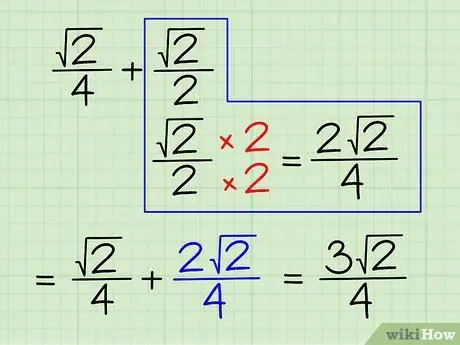
Step 5. Work on Example 5
Try adding and subtracting the square root that is part of the fraction. Like ordinary fractions, you can only add or subtract fractions that have the same denominator. Say the problem is: (√2)/4 + (√2)/2. Here's how to solve it:
- Change these terms so that they have the same denominator. The least common multiple (LCM), which is the smallest number that is divisible by two related numbers, of the denominators "4" and "2," is "4."
- So change the second term, (√2)/2 so that the denominator is 4. You can multiply the numerator and denominator of the fraction by 2/2. (√2)/2 x 2/2 = (2√2)/4.
- Add the two numerators together if the denominators are the same. Work like adding ordinary fractions. (√2)/4 + (2√2)/4 = 3√2)/4.
Tips
All square roots that have a perfect square factor must be simplified before begin to identify and combine common radicans.
Warning
- Never combine unequal square roots.
-
Never combine integers with square roots. That is, 3 + (2x)1/2 can not simplified.
Note: sentence "(2x) to the power of half" = (2x)1/2 just another way of saying "root (2x)".






