- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
You might think integers are just ordinary numbers, like 3, -12, 17, 0, 7000, or -582. Integers are also called whole numbers because they are not divided into parts like fractions and decimals. Read this article to learn everything you need about adding and subtracting integers, or read directly the section you need.
Step
Method 1 of 5: Adding and Subtracting Positive Integers Using a Number Line

Step 1. Understand about the number line
Number lines turn basic math into something tangible and physical that you can see. With just a few signs and common sense, we can use it like a calculator to add and subtract numbers.

Step 2. Draw a base number line
Imagine or draw an even straight line. Make a dot in the middle of your line. Write 0 or zero next to this period.
Your math book might call this the starting point because it is the starting point for all numbers

Step 3. Draw two dots, one each to the right and left of your zero
Write -1 next to the dot to the left and
Step 1. next to the dot on the right. This is the integer closest to zero.
- Don't worry about making the distances between the points exactly the same - as long as you know what each point means, a number line can be used.
- The left side is the beginning of the sentence.

Step 4. Complete your number line by adding more numbers
Make more dots to the left than -1 and to the right than 1. To the left, from -1, mark your dots with -2, -3, and -4. To the right, from 1, mark your dot with
Step 2
Step 3., da
Step 4.. You can continue if you have space on your paper.
The example in the figure shows a number line from -6 to 6

Step 5. Understand about positive and negative integers
Positive integers, also called natural number, is an integer greater than zero. 1, 2, 3, 25, 99, and 2007 are positive integers. Negative integers are integers that are less than zero (such as -2, -4, and -88).
Integers are another way of calling whole numbers. Fractions like 1/2 (half) are only part of the number, so they are not integers. Same as decimal, for example 0.25 (zero point two five); decimal is not an integer

Step 6. Start solving 1+2 by placing your finger on point 1
We will solve simple addition problems 1+2 using the number line you just created. The first number is
Step 1., so start putting your finger on the number.
-
Is this question too easy?
If you've ever added, you probably know the answer to 1+2. Good: if you know the result, it will be easier to understand how the number line works. Then, you can use the number line to solve more difficult addition problems or prepare for more difficult math like algebra.

Step 7. Add up 1+2 by moving your finger 2 dots to the right
Slide your finger to the right, counting the number of dots (another number) that you pass. If you have passed 2 new points, stop. The number your finger is pointing at is the answer,
Step 3

Step 8. Add any positive integers by moving to the right on the number line
Suppose we want to solve 3+2. Start at 3, move to the right or add 2 dots. We stop at 5. The problem is written 3 + 2 = 5.

Step 9. Subtract positive integers by moving left on the number line
For example, we want to solve 6 -4, we start at 6, move to the left 4 points, and stop at 2. This problem is written 6 - 4 = 2.
Method 2 of 5: Adding and Subtracting Negative Numbers Using a Number Line

Step 1. Learn about number lines
If you don't know how to create a number line, return to the Adding and Subtracting Positive Numbers Using Number Lines section to learn how to create one.
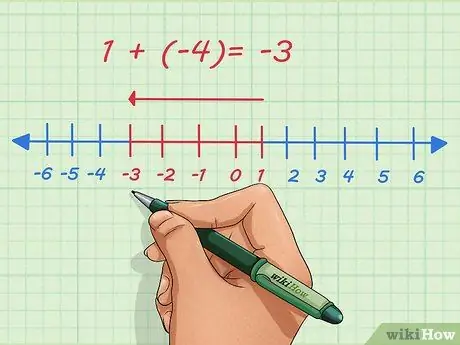
Step 2. Understand about negative numbers
Positive numbers are indicated by the direction to the right on the number line. Negative numbers are indicated to the left on the number line. Adding negative numbers means moving the point to the left on the number line.
-
For example, let's add 1 and -4. Usually, this question is written like this:
1 + (-4)
. On the number line, we start at 1, move 4 points to the left and stop at -3.
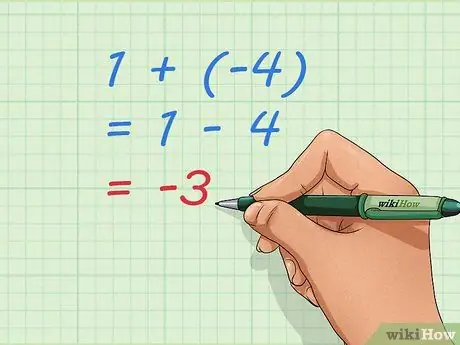
Step 3. Use basic equations to understand the addition of negative numbers
Notice that -3, our answer, is the number we will get if we do 1 - 4. Adding 1 + (-4) and subtracting 4 from 1 is the same problem. We can write it as an equation, a mathematical sentence that shows equality:1 + (-4) = 1 - 4 = -3
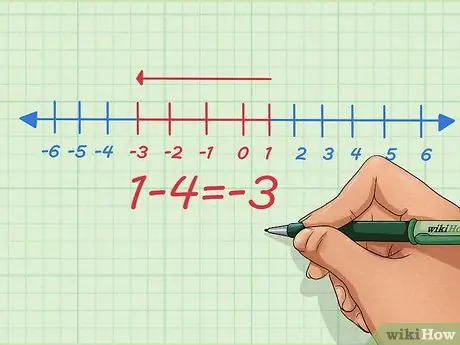
Step 4. Instead of adding negative numbers, turn it into a subtraction problem using positive numbers
As we can see from the simple equation above, we can do both - turn the addition of negative numbers into subtraction of positive numbers and vice versa. You may have been taught to turn negatives into negatives without knowing why - here's why.
-
For example, -4. When we add -4 and 1, we subtract 1 by 4. It can be written in math by writing
1 + (-4) = 1 - 4
. We can write this on the number line, starting at our starting point at 1, then adding 4 dots to the left (in other words, adding -4). Since this is an equation, one thing is equal to another - so the opposite is also true
1 - 4 = 1 + (-4)
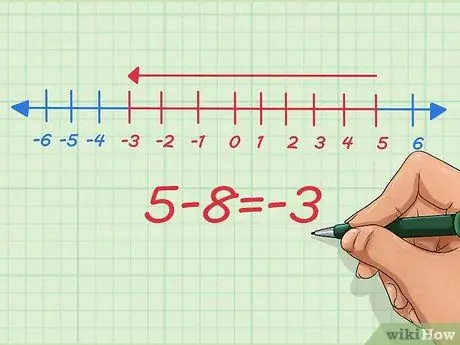
Step 5. Understand how to subtract negative numbers on a number line
On the number line, subtracting negative numbers is the same as reducing length. Let's start with 5 - 8.
On the number line, we start at our starting point at 5, subtract 8, and stop at -3
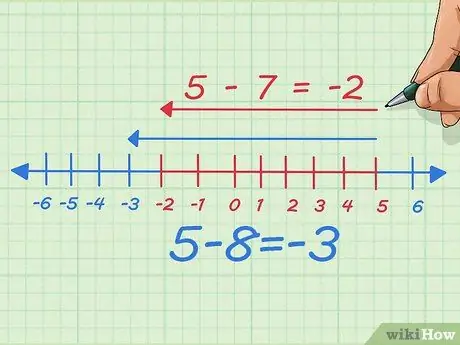
Step 6. Subtract the amount you are subtracting and see what happens
Suppose we subtract one, the number we subtract, or in other words subtract 7 instead of 8. Now we subtract one point to the left on the number line. In writing, we started with 5 - 8 = -3 Now, we just moved 7 to the left, so it becomes 5 - 7 = -2
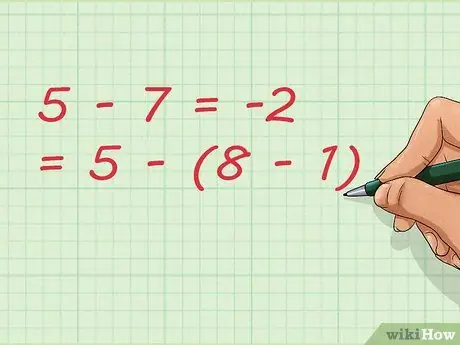
Step 7. Notice that subtracting can result in addition
In our example, we are subtracting the number 1. In writing the equation, we can write it shorter like: 5 - 7 = -2 = 5 - (8 - 1)

Step 8. Convert negative signs to positive when adding negative numbers
Using the step of converting all subtractions to additions, we can write in a shorter way like: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
We already know that 5 - 8 = -3, so take 5 - 8 out of the equation and enter -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
We already know that 5 - (8 - 1) is - subtracts one point from 5 - 8. Our equation can show that 5 - 8 equals -3, and subtracting one point gives -2. The equation can be written like this:
-3 - (-1) = -3 + 1
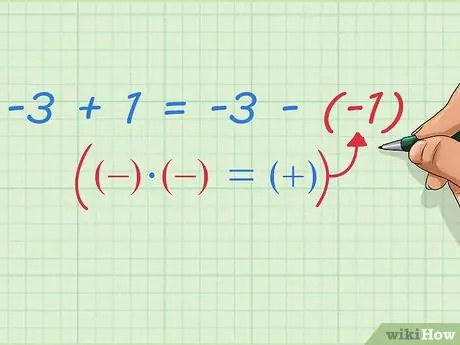
Step 9. Write the subtraction of negative numbers as addition
Notice what happens after this - we've already proved that: -3 + 1 = -3 - (-1)We can write this with simpler and more general math writing rules: first number plus second number = first number minus (negative second number) Or, a simpler way you've probably heard in math class: Change the two negative signs into a positive sign.
Method 3 of 5: Adding Positive Large Integers

Step 1. Write the addition problem of 2,503 + 7,461 with one number over the other
Write down the numbers in the large column so that 2 is over 7, 5 is over 4, and so on. In this way, we will learn how to add integers that are too large to imagine or use the number line.
Write a + sign to the left of the number below and the line below it, as you might learn for smaller addition problems
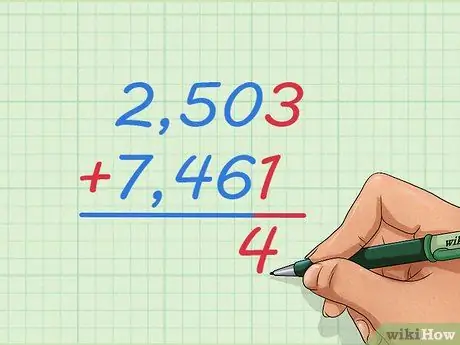
Step 2. Start by adding up the two numbers on the far right
It might be a little strange to start from the right because we read numbers from the left. We have to add from the right to get the correct answer, which you can see later.
-
Under the two rightmost numbers,
Step 3. da
Step 1., write down the sum of the two
Step 4..

Step 3. Add up each number in the column in the same way
Move to the left, add up 0+6, 5+4, and 2+7. Write the answer under each pair of numbers.
Your answer should be: 9.964. Check your work if you make a mistake.

Step 4. Now add up 857+135
You'll notice something different as soon as you add up the first pair of numbers on the right. 7+5 equals 12, a two-digit number, but you can only write one digit under that column. Keep reading to find out what you should do and why you should always start from the right and not from the left.

Step 5. Add up 7+5 and learn where to write the answer
7+5=12, but you can't put 1 and 2 under the line. But, write down the last digit,
Step 2., under the line and write down the first digit
Step 1., above the column to the left, 5+3.
-
If you're curious about how it works, think about what splitting 1 and 2 means. You're actually dividing 12 into
Step 10. da
Step 2.. You can write 10 above the number if you want, and you'll see 1 in columns 5 and 3, just like before.

Step 6. Add up 1+5+3 to get the next digit of the answer
Now you have three digits to add up because you added 1 to this column. The answer is
Step 9., so your answer becomes 92.

Step 7. Complete the problem as usual
Keep working the digits to the left until you've added up all the numbers, in this case, there's only one column left. Your final answer should be 992.
- You can try more complicated questions, like 974+568. Remember, whenever you get a two-digit number, only write the last digit as the answer and place the other digit above the column to the left of it, which you will add up next. If the answer in the last column (far left) contains two digits, write it down as your answer.
- See the Tips section for answers to questions 974+568 once you've tried to solve them.
Method 4 of 5: Subtracting Positive Large Integers

Step 1. Write the subtraction problem 4.713 - 502 with the first number above the second number
Write it so that 3 is directly above 2, 1 is above 0, 7 is above 5, and 4 is above the blank.
You can write 0 under 4 if this helps you remember which number is above which number. You can always add a 0 in front of a number without changing it. Make sure to add it before the number, not after it

Step 2. Subtract each number below from the number directly above it
Always start from the right. Solve 3-2, 1-0, 7-5, and 4-0, write the answer to each question directly below the two numbers that are subtracted.
The result is, 4.211.

Step 3. Now write questions 924 - 518 in the same way
These numbers have the same number of digits, so you can write them down easily. This problem will teach you something about subtracting integers if you don't already know it.

Step 4. Learn how to solve the first problem, which is on the far right
4 - 8. This problem is complicated because 4 is less than 8, but don't use negative numbers, but follow these steps:
- In the top row, cross 2 and write 1. 2 should be to the left of 4.
- Cross 4 and write 14. Do this in a narrow space so that it is clear that 14 is over 8. You can also write 1 in front of 4 to make 14 if there is enough space.
- What you've just done is borrow 1 from the tens place or the second column from the right and convert it to 10 in the ones place or the far right column. Once the number 10 is equal to ten times the number 1, so it's the same.

Step 5. Now solve problems 14 - 8 and write the answer under the rightmost column
It should have written 6 on the rightmost answer line.

Step 6. Complete the next column to the left, using the new number you wrote down
The subtraction should be 1 - 1, which is equal to 0.
Your answer should now be 06.

Step 7. Solve the problem by completing the last subtraction, the leftmost column
9 - 5 = 4, so your final answer is 406.

Step 8. Now we solve the problem of subtracting large numbers from small numbers
Suppose you are asked to complete 415,990 - 968,772. Write the second number under the first number and you will realize that the number below is bigger! You can tell immediately from the first digit on the left: 9 is greater than 4, so numbers starting with 9 are bigger.
Make sure you write down the column correctly before comparing. 912 no greater than 5000 you can tell if you write the column correctly because there are no numbers below 5. You can add zero help, for example, write 912 with 0912 so that the column equals 5000.

Step 9. Write the smaller number under the larger number and add a - sign in front of the answer
Whenever you subtract a number from a smaller number, the result is a negative number. It's better to write this sign before subtracting so you don't forget to write it down.

Step 10. To answer, subtract the small number from the large number and remember to write the - sign
Your answer will be negative, which is indicated by a - sign. Do not tries to subtract a large number from a small number, then makes the result negative; your answer will be wrong.
The new problem to solve is: 968,772 - 415,990 = -? See the Tips section for the answer after trying to solve this problem
Method 5 of 5: Adding and Subtracting Negative Integers
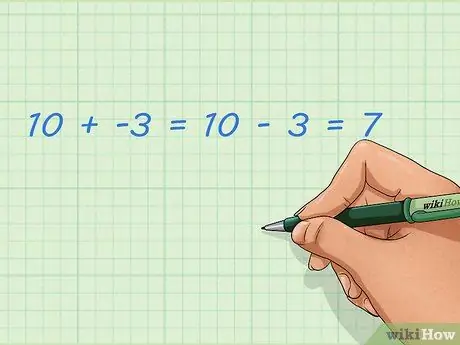
Step 1. Learn how to add negative and positive numbers
Adding negative integers is the same as subtracting positive integers. This is easier to do with the number line described in another section, but you can think of it in words too. Negative numbers are not ordinary numbers; this number is less than zero and can represent the amount taken. If you add this take to a regular number, the result becomes smaller.
- Example: 10 + -3 = 10 - 3 = 7
- Example: -12 + 18 = 18 + -12 = 18 - 12 = 6. Remember that you can always change the order of numbers in addition, but not in subtraction.
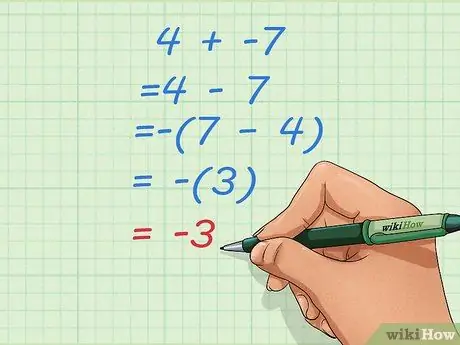
Step 2. Learn what you have to do if you turn it into a subtraction problem with a smaller starting number
Sometimes, changing addition to subtraction problems like the one above can lead to weird answers like 4 - 7. When this happens, reverse the order of the numbers and make your result negative.
- Let's say your initial problem is 4 + -7.
- Turn it into a subtraction problem: 4 - 7
- Reverse the order and make the result negative: -(7 - 4) = -(3) = -3.
- If you're not familiar with using brackets in equations, think about this: 4 - 7 turns into 7 - 4 with the addition of a negative sign. 7 - 4 = 3, but we have to change it to -3 so that the answer to questions 4 - 7 is correct.
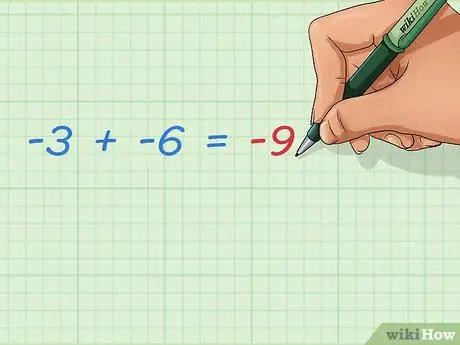
Step 3. Learn how to add two negative integers
Two negative numbers added together always makes the negative result bigger. Since no positive numbers are added, the result will be further away from 0. The answer is easy:
- -3 + -6 = -9
- -15 + -5 = -20
- Do you see the pattern? All you have to do is add up the numbers as if they were positive numbers and add a negative sign. -4 + -3 = -(4 + 3) = -7
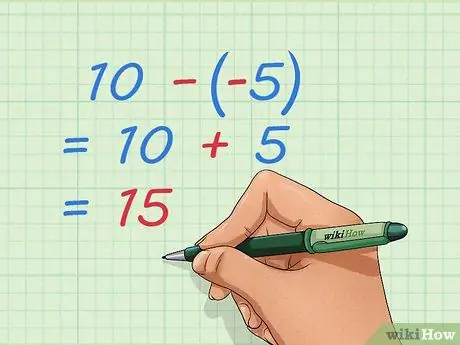
Step 4. Learn how to subtract negative integers
Like the addition problem, you can rewrite the problem so that you only have positive numbers. If you subtract negative numbers, you take away some of the things that have already been taken, which is the same as adding positive numbers.
- Think of negative numbers as stolen money. If you subtract or take away stolen money so you can return it, it's like giving money to someone, right?
- Example: 10 - -5 = 10 + 5 = 15
- Example: -1 - -2 = -1 + 2. You already learned how to solve this problem in the first step, remember? Reread how to add negative and positive numbers if you forgot.
- Here's the complete solution of the last example: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Tips
- You may have written long numbers like 2,521,301 using commas (,) instead of (.) depending on where you live. Use what your teacher asks you to so you don't get confused with other writing systems.
- Draw your number lines on different scales to represent different numbers. There's no rule that every distance on a number line equals 1. Imagine a number line that's 10 instead of 1. Apart from the fact that every point is 10 now, addition and subtraction remain the same. Try it if you don't believe it.
- If you try the special challenge questions in the Long Numbers section, here's the answer: 974 + 568 = 1.542. The answer from 415,990 - 968,772 is -552.782.






