- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-06-01 06:05.
Subtracting fractions from integers is not as difficult as it seems. There are two main ways to do this: you can convert an integer to a fraction, or you can subtract 1 from the whole number and turn 1 into a fraction with the same base as the subtracting fraction. Once you have two fractions with the same base, you can start subtracting. Either way will allow you to quickly and easily subtract fractions from whole numbers. If you want to know how to do it, see Step 1 to get started.
Step
Method 1 of 2: Converting Integers to Fractions

Step 1. Write down the problem
Suppose you subtract the fraction 2/7 from the integer 6. All you need to know is that the top part of a fraction is called the numerator and the bottom part of a fraction is called the denominator. Write the following questions: 6 - 2/7 = ?

Step 2. Convert whole numbers to fractions
6 can be rewritten as 6/1 because 6/1 is equal to 1 6 times, or just the number 6. You can place any integer above 1 and the value will not change. This only helps to put integers in the same form as fractions. Now, your problem will be: 6/1 - 2/7 = ?
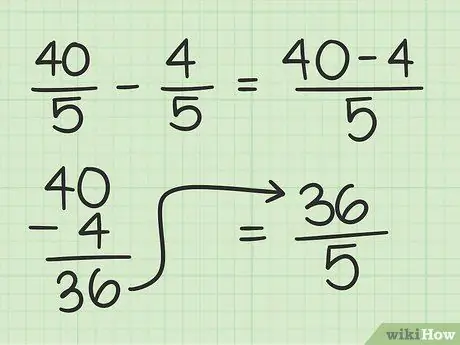
Step 3. Multiply the numerator and denominator of the initial whole number by the denominator of the initial fraction and then subtract the two fractions
You have to make 6/1 and 2/7 have the same base to subtract the two terms. To do this, you'll need to multiply the numerator and denominator 6/1 by 7. This is a quick way to find the LCM, or the smallest multiple, of the two fractions' denominators, 1 and 7. 7 is the smallest number that is divisible by 1 and 7. both fractions have the same denominator, you can subtract the numerator of the fraction by leaving the value of the denominator the same, to get the final answer. Here's how you do it:
-
First, multiply 6/1 by 7/7:
6/1 x 7/7 = 42/7
-
Next, subtract the denominator of both fractions:
42/7 - 2/7 = (42-2)/7 = 40/7

Step 4. Write down your final answer
If you want your answer in the form of a common fraction (where the numerator is greater than the denominator), then you're done. If you want your answer to be a mixed number, where you write your final answer as one whole number and one fraction, then all you have to do is divide the numerator by the denominator, make the quotient as the whole number, and put the remainder over the initial denominator and the denominator that remains as your fraction. Here's what you do:
- First, divide 40 by 7. 40 divided by 7 equals 5, with a remainder of 5. That's because 7 x 5 = 35. When you subtract 35 from 40, you have a subtraction of 5, or a remainder of 5.
- Next, write down your integer: 5.
- Take the remainder, also 5, and place it over the original denominator to get 5/7.
- Write down the whole number, followed by the new fraction. You get 5 5/7. Thus, the common fraction 40/7 is rewritten as a mixed number 5 5/7.
Method 2 of 2: Subtract 1 from the First Integer

Step 1. Write down the problem
This will be useful if you know that you want to write your answer as a mixed number. This way, will make it easier for you to get the final result. Let's use the same equation from the first method, to see if you can use either method in any situation. Write down the following questions:
6 - 2/7 = ?

Step 2. Subtract 1 from the whole number
Just subtract 1 from 6 to get 5. Write down this number.
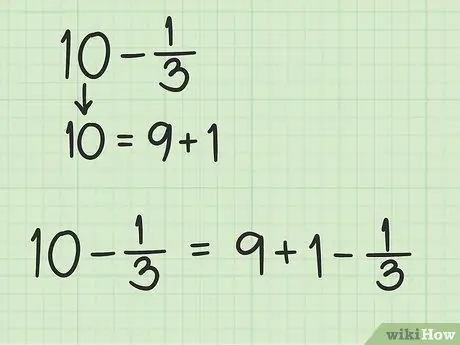
Step 3. Convert 1 to a fraction with the same base as the fraction
You need to convert 1 to a fraction with the same denominator as 7 at 2/7, so you can subtract 2/7 from the number. Now, you can imagine 1 as 1/1, and then consider the number you have to multiply by the denominator and the numerator 1/1 so that the fractions have a denominator of 7 but have the same value. The LCM, or the largest multiple of the denominators of 1 and 7, is 7, because 7 is the smallest number that is divisible by 1 and 7.
- So, multiply 1/1 by 7/7 to get 7/7.
- Note that 7/7 has the same value as 1/1.

Step 4. Write down your new problem
Now, the problem you have is 5 7/7 - 2/7. This makes the numbers easier to work with.

Step 5. Subtract the second fraction from the first
Now, just subtract 2/7 from 7/7. When subtracting fractions, the denominator must remain the same, while you subtract the second numerator from the first. So, 7/7 - 2/7 = (7-2)/7 = 5/7.
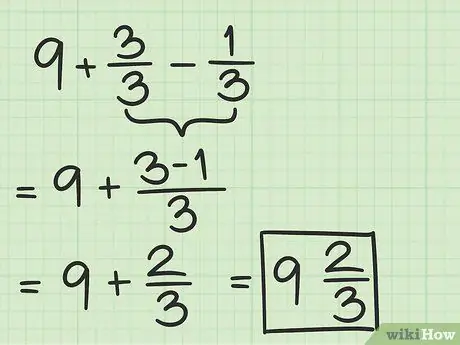
Step 6. Write down the whole number with its fraction to get your final answer
You've already written 5, and you can just add 2/7 next to it. Thus, 6 - 2/7 = 5 5/7. This method is a bit easier if you want your answer to be mixed numbers, because you only have to work with integers 1 instead of whole 6, and you don't have to convert from common fractions to mixed numbers, as you did in the first method. You can determine which method is more suitable for your needs.






