The vertex of a quadratic or parabola equation is the highest or lowest point of the equation. This point is inside the symmetrical plane of the parabola; whatever is to the left of the parabola is a perfect reflection of whatever is to the right. If you want to find the vertex of a quadratic equation, you can use the vertex formula or complete the square.
Step
Method 1 of 2: Using the Peak Formula
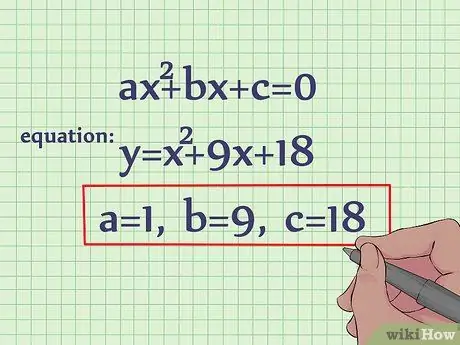
Step 1. Determine the values of a, b, and c
In a quadratic equation, the x. part2 = a, part x = b, and constant (part without variables) = c. For example, you want to solve the following equation: y = x2 + 9x + 18. In this example, a = 1, b = 9, and c = 18.
Step 2. Use the vertex formula to find the x-value of the vertex
The vertex is also a symmetrical equation. The formula for finding the x value of the vertex of a quadratic equation is x = -b/2a. Enter the required value to find x. Enter the values of a and b. Write down how you work:
- x=-b/2a
- x=-(9)/(2)(1)
- x=-9/2
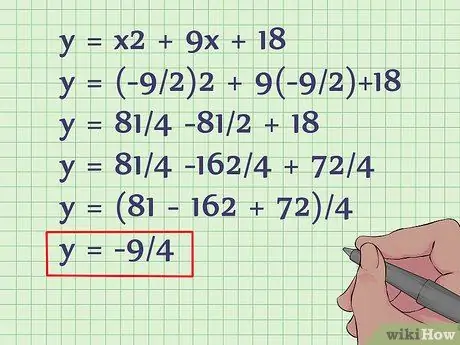
Step 3. Plug the value of x into the original equation to get the value of y
If you already know the value of x, plug it into the original equation for the value of y. You can think of the formula for finding the vertex of a quadratic equation as (x, y) = [(-b/2a), f(-b/2a)]. This means, to find the value of y, you have to find the value of x using a formula and plug it back into the equation. Here's how to do it:
- y = x2 + 9x + 18
- y = (-9/2)2 + 9(-9/2) +18
- y = 81/4 -81/2 + 18
- y = 81/4 -162/4 + 72/4
- y = (81 - 162 + 72)/4
- y = -9/4
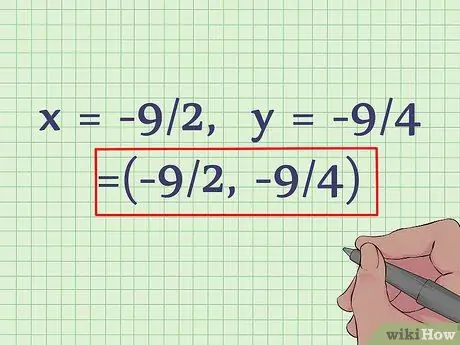
Step 4. Write down the values of x and y as consecutive pairs
If you already know that x = -9/2 and y = -9/4, write them as consecutive pairs: (-9/2, -9/4). The vertex of the quadratic equation is (-9/2, -9/4). If you draw this parabola on a graph, this point is the minimum/lowest point of the parabola because x2 positive.
Method 2 of 2: Complete the Square
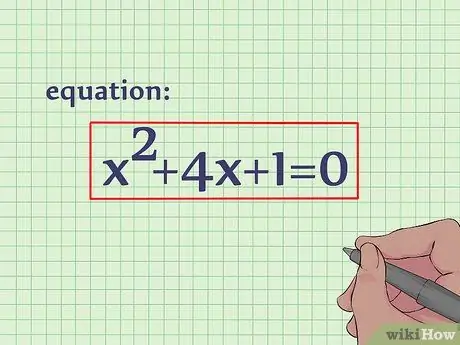
Step 1. Write down the equation
Completing the square is another way to find the vertex of a quadratic equation. Using this method, if you work your way up to the end, you can find the x and y coordinates directly, without having to plug the x coordinates into the original equation. If you want to solve the following quadratic equation: x2 + 4x + 1 = 0.
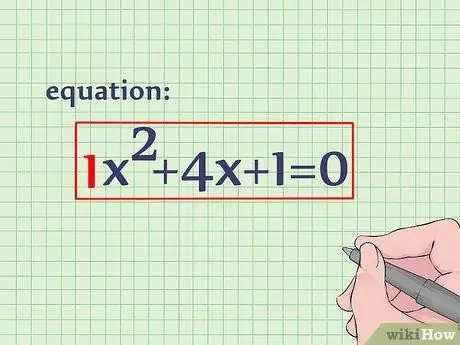
Step 2. Divide each part by the coefficient of x2.
In this case, the coefficient of x2 is 1, so you can skip this step. Dividing all parts by 1 will not change anything.
Step 3. Move the constants part to the right side of the equation
A constant is the part that has no coefficients. In this case, the constant is 1. Move 1 to the other side of the equation by subtracting 1 from both sides. Here's how to do it:
- x2 + 4x + 1 = 0
- x2 + 4x + 1 -1 = 0 - 1
- x2 + 4x = - 1
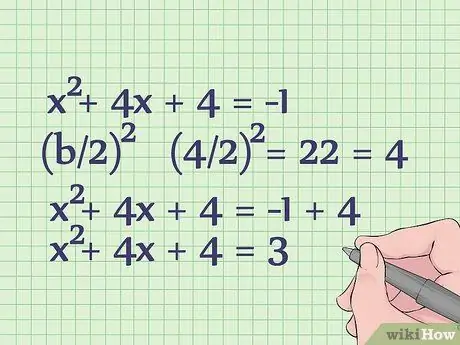
Step 4. Complete the square on the left side of the equation
To do so, find (b/2)2 and add the result to both sides of the equation. Enter 4 for b because 4x is part of b in this equation.
-
(4/2)2 = 22 = 4. Now, add 4 to both sides of the equation to get something like this:
- x2 + 4x + 4 = -1 + 4
- x2 + 4x + 4 = 3
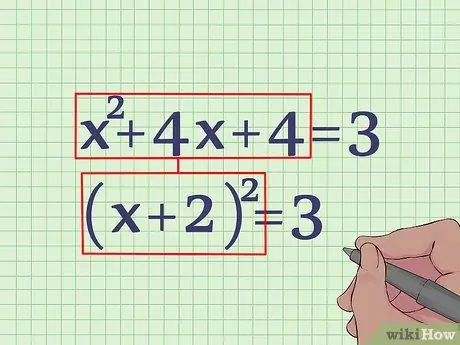
Step 5. Factor the left side of the equation
You can see that x2 + 4x + 4 is a perfect square. This equation can be written as (x + 2)2 = 3
Step 6. Use this shape to find the x and y coordinates
You can find the x-coordinate by making (x + 2)2 equals zero. So, when (x + 2)2 = 0, what is the value of x? The x variable must be -2 to compensate for +2, so your x-coordinate is -2. Your y-coordinate is the constant on the other side of the equation. So, y = 3. You can also shorten it and replace the number in parentheses to get the x-coordinate. So, the vertex of the equation x2 + 4x + 1 = (-2, -3)
Tips
- Determine a, b, and c correctly.
- Always write down how you work. Not only does this help the person giving you a rating know if you understand what you're doing, but it also helps you check if you made any mistakes.
- The order of calculation operations must be followed for the results to be correct.
Warning
- Write it down and check how you work!
- Make sure you know a, b, and c – otherwise your answer will be wrong.
- Don't get frustrated – this may take some practice.
