- Author Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- Last modified 2025-06-01 06:05.
When represented graphically, the quadratic equation is of the form ax2 + bx + c or a(x - h)2 + k form the letter U or an inverted U curve called a parabola. Graphing a quadratic equation is looking for the vertex, direction, and often the x and y intersection. In cases of fairly simple quadratic equations, entering a set of x values and plotting the curve based on the resultant points may be sufficient. See Step 1 below to get started.
Step

Step 1. Determine the form of the quadratic equation you have
Quadratic equations can be written in three different forms: general form, vertex form, and quadratic form. You can use any form to graph a quadratic equation; the process of depicting each graph is slightly different. If you're doing homework, you'll usually receive questions in one of these two forms - in other words, you won't be able to choose, so it's best to understand both. The two forms of the quadratic equation are:
-
General form.
In this form, the quadratic equation is written as: f(x) = ax2 + bx + c where a, b, and c are real numbers and a is not zero.
For example, two quadratic equations of general form are f(x) = x2 + 2x + 1 and f(x) = 9x2 + 10x -8.
-
Peak shape.
In this form, the quadratic equation is written as: f(x) = a(x - h)2 + k where a, h, and k are real numbers and a is not zero. It is called the vertex form because h and k will immediately give the vertex (midpoint) of your parabola at the point (h, k).
The two vertex form equations are f(x) = 9(x - 4)2 + 18 and -3(x - 5)2 + 1
- To graph any type of equation, we must first find the vertex of the parabola, which is the midpoint (h, k) at the end of the curve. The coordinates of the peaks in the general form are calculated by: h = -b/2a and k = f(h), while in the peak form, h and k are in the equation.
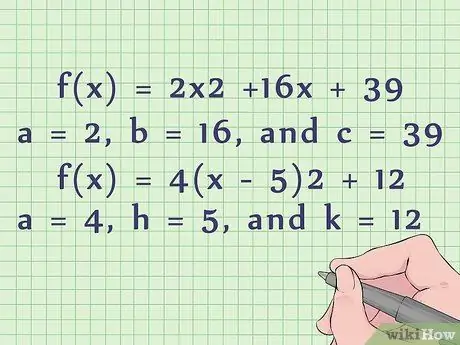
Step 2. Define your variables
In order to solve a quadratic problem, the variables a, b, and c (or a, h, and k) usually have to be defined. An ordinary algebra problem will give a quadratic equation with the available variables, usually in general form, but sometimes in peak form.
- For example, for an equation of general form f(x) = 2x2 +16x + 39, we have a = 2, b = 16, and c = 39.
- For the peak form equation f(x) = 4(x - 5)2 + 12, we have a = 4, h = 5, and k = 12.

Step 3. Calculate h
In the vertex form equation, your h value is already given, but in the general form equation, the h value must be calculated. Remember that, for equations of general form, h = -b/2a.
- In our general form example (f(x) = 2x2 +16x + 39), h = -b/2a = -16/2(2). After solving, we find that h = -4.
- In our vertex form example (f(x) = 4(x - 5)2 + 12), we know that h = 5 without doing any math.
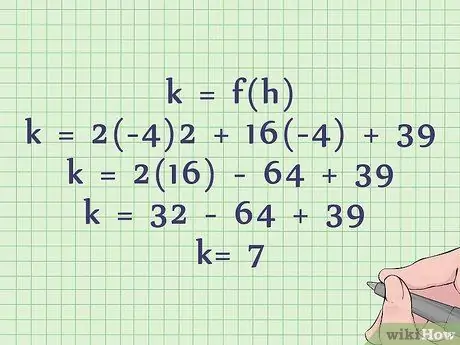
Step 4. Calculate k
Like h, k is already known in the equation of the peak form. For equations of general form, remember that k = f(h). In other words, you can find k by replacing all the x values in your equation with the h values you just found.
-
We have already determined in our general form example that h = -4. To find k, we solve our equation by plugging in our value of h in place of x:
- k = 2(-4)2 + 16(-4) + 39.
- k = 2(16) - 64 + 39.
-
k = 32 - 64 + 39 =
Step 7.
- In our peak form example, again, we know the value of k (which is 12) without having to do any math.
Step 5. Draw your peak
The vertex of your parabola is the point (h, k) - h represents the x-coordinate, while k represents the y-coordinate. The vertex is the midpoint of your parabola - either at the bottom of the U or at the top of the inverted U. Knowing the vertices is an important part of drawing a precise parabola - often, in schoolwork, determining the vertex is the part to look for in a question.
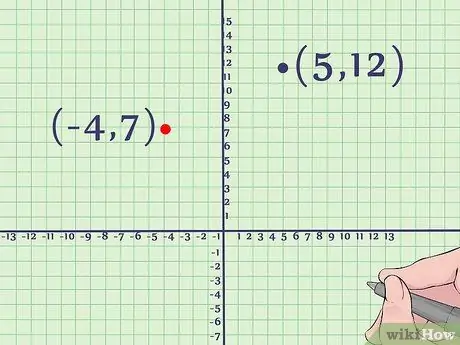
- In our general form example, our peak is (-4, 7). Thus, our parabola will culminate 4 steps to the left from 0 and 7 steps above (0, 0). We must depict this point in our graph, making sure to mark the coordinates.
- In our vertex form example, our vertex is (5, 12). We have to draw a point 5 steps to the right and 12 steps above (0, 0).
Step 6. Draw the axis of the parabola (optional)
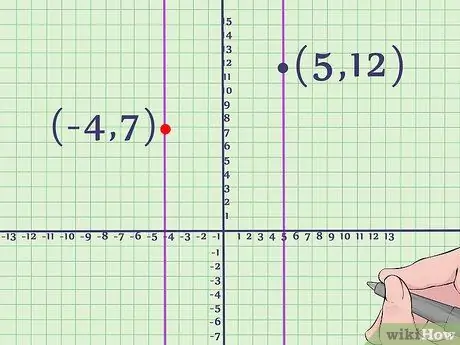
The axis of symmetry of a parabola is a line that passes through its center, which divides it exactly in the middle. On this axis, the left side of the parabola will reflect the right side. For quadratic equations in the form ax2 + bx + c or a(x - h)2 + k, the axis of symmetry is the line that is parallel to the y-axis (in other words, exactly vertical) and passes through the vertex.
In the case of our general form example, the axis is the line parallel to the y-axis and passing through the point (-4, 7). Even though it's not part of the parabola, thinly marking this line on your graph will eventually help you see the symmetrical shape of the parabola's curve
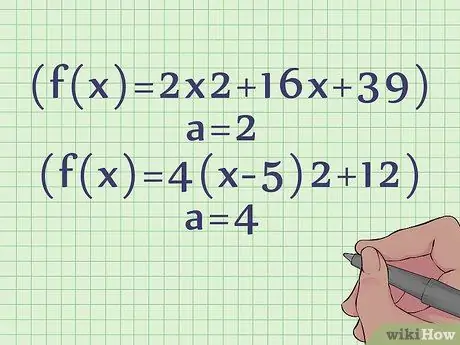
Step 7. Find the direction of the opening of the parabola
After knowing the peak and axis of the parabola, next we need to know if the parabola opens up or down. Fortunately, this is easy. If the value of a is positive, the parabola will open upwards, whereas if the value of a is negative, the parabola will open downwards (i.e. the parabola will be inverted).
- For our general form example (f(x) = 2x2 +16x + 39), we know that we have a parabola that opens up because, in our equation, a = 2 (positive).
- For our vertex form example (f(x) = 4(x - 5)2 + 12), we know that we also have a parabola that opens up because a = 4 (positive).
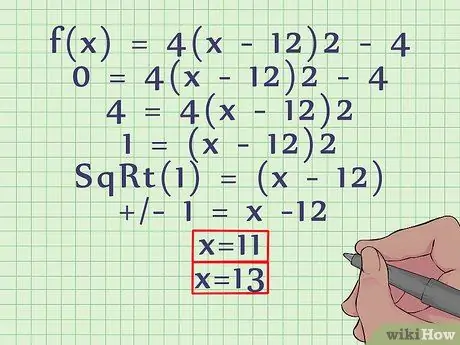
Step 8. If needed, find and draw the x-intercept
Often, in schoolwork, you will be asked to find the x-intercept in the parabola (which is one or two points where the parabola meets the x-axis). Even if you don't find one, these two points are very important for drawing a precise parabola. However, not all parabolas have an x-intercept. If your parabola has a vertex that opens up and its vertex is above the x-axis or if it opens downwards and its vertex is below the x-axis, the parabola will have no x-intercept. Otherwise, solve your x-intercept in one of the following ways:
-
Just make f(x) = 0 and solve the equation. This method can be used for simple quadratic equations, especially in peak form, but will be very difficult for complex equations. See below for an example
- f(x) = 4(x - 12)2 - 4
- 0 = 4(x - 12)2 - 4
- 4 = 4(x - 12)2
- 1 = (x - 12)2
- Root (1) = (x - 12)
- +/- 1 = x -12. x = 11 and 13 is the x-intercept in the parabola.
-
Factor your equation. Some equations in the form ax2 + bx + c can easily be factored into the form (dx + e)(fx +g), where dx × fx = ax2, (dx × g + fx × e) = bx, and e × g = c. In this case, your x-intercepts are x values which will make any term in parentheses = 0. For example:
- x2 + 2x + 1
- = (x + 1)(x + 1)
- In this case, your only x-intercept is -1 because making x equal -1 will make any factor term in parentheses equal 0.
-
Use the quadratic formula. If you can't easily solve your x-intercept or factor your equation, use a special equation called a quadratic formula that was created for this purpose. If not solved, convert your equation to the form ax2 + bx + c, then enter a, b, and c into the formula x = (-b +/- sqrt(b)2 - 4ac))/2a. Note that this method often gives you two answers for the value of x, which is OK - it just means that your parabola has two x-intercepts. See below for an example:
- -5x2 + 1x + 10 is put into the quadratic formula like this:
- x = (-1 +/- Root (1.)2 - 4(-5)(10)))/2(-5)
- x = (-1 +/- Root(1 + 200))/-10
- x = (-1 +/- Root(201))/-10
- x = (-1 +/- 14, 18)/-10
- x = (13, 18/-10) and (-15, 18/-10). The x-intercept in the parabola is x = -1, 318 and 1, 518
- Our previous example of the general form, 2x2 +16x+39 is put into the quadratic formula as follows:
- x = (-16 +/- Root(162 - 4(2)(39)))/2(2)
- x = (-16 +/- Root(256 - 312))/4
- x = (-16 +/- Root(-56)/-10
- Since it is impossible to find the square root of a negative number, we know that this parabola has no x-intercept.
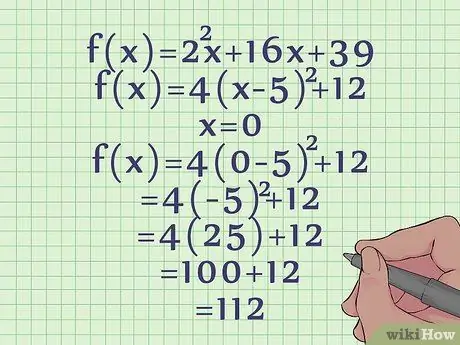
Step 9. If needed, find and draw the y-intercept
While it's often not necessary to look for the y-intercept in equations (the point where the parabola passes through the y-axis), you may eventually have to find it, especially if you're in school. The process is fairly simple - just make x = 0, then solve your equation for f(x) or y, which gives the value of y where your parabola passes through the y-axis. Unlike the x-intercept, a regular parabola can have only one y-intercept. Note - for equations of general form, the y-intercept is at y = c.
-
For example, we know that our quadratic equation is 2x2 + 16x + 39 has a y-intercept at y = 39, but this can also be found in the following way:
- f(x) = 2x2 +16x+39
- f(x) = 2(0)2 + 16(0) + 39
-
f(x) = 39. The y-intercept of the parabola is at y = 39.
As noted above, the y-intercept is at y = c.
-
The form of our vertex equation is 4(x - 5)2 + 12 has a y-intercept which can be found in the following way:
- f(x) = 4(x - 5)2 + 12
- f(x) = 4(0 - 5)2 + 12
- f(x) = 4(-5)2 + 12
- f(x) = 4(25) + 12
-
f(x) = 112. The y-intercept of the parabola is at y = 112.
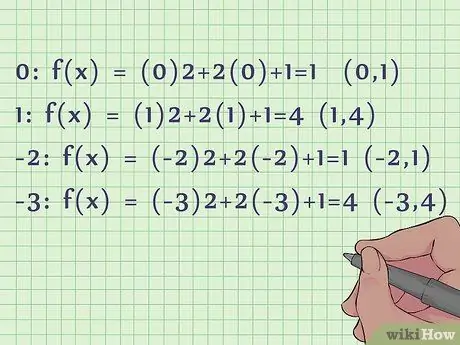
Step 10. If needed, draw additional points, then draw a graph
Now you have the vertex, direction, x-intercept, and possibly, y-intercept in your equation. At this stage, you can try to draw your parabola using the points you have as a guide, or look for other points to fill in your parabola so that the curve you draw is more precise. The easiest way to do this is to simply enter some x-values in any side of your vertex, then plot these points using the y-values you get. Oftentimes, teachers ask you to look for several points before drawing your parabola.
-
Let's review the equation x2 + 2x + 1. We already know that the x-intercept is only at x = -1. Since the curve only touches the x-intercept at one point, we can conclude that the vertex is its x-intercept, which means that the vertex is (-1, 0). We effectively only have one point for this parabola - not enough to draw a good parabola. Let's look for some other points to make sure that we're drawing a thorough graph.
- Let's find the y values for the following x values: 0, 1, -2, and -3.
- For 0: f(x) = (0)2 + 2(0) + 1 = 1. Our point is (0, 1).
-
For 1: f(x) = (1)2 + 2(1) + 1 = 4. Our point is (1, 4).
- For -2: f(x) = (-2)2 + 2(-2) + 1 = 1. Our point is (-2, 1).
-
For -3: f(x) = (-3)2 + 2(-3) + 1 = 4. Our point is (-3, 4).
- Draw these points on the graph and draw your U-shaped curve. Note that the parabola is perfectly symmetrical - when your points on one side of the parabola are integers, you can usually reduce the work of simply reflecting a given point on the parabola's axis of symmetry to find the same point on the other side of the parabola.
Tips
- Round numbers or use fractions according to your algebra teacher's request. This will help you better graph the quadratic equation.
- Note that in f(x) = ax2 + bx + c, if b or c is equal to zero, these numbers will disappear. For example, 12x2 + 0x + 6 becomes 12x2 + 6 because 0x is 0.






