A circle is a two-dimensional shape created by depicting a curve. In trigonometry and other fields of mathematics, a circle is understood as a particular kind of line: a line that forms a closed loop, with each point on the line equidistant from a fixed point in the center of the circle. Drawing the graph is easy. Just start with Step 1.
Step
Part 1 of 2: Understanding the Mathematical Properties of Circles
Step 1. Record the center of the circle
The center of a circle is a point inside the circle that is equidistant from all points on the line.
Step 2. Know how to find the radius of a circle
The radius is the equal and constant distance from all points on the line to the center of the circle. In other words, the radius is all the line segments that connect the center of the circle to any point on the curved line.
Step 3. Know how to find the diameter of a circle
Diameter is the length of the line segment that joins two points on the circle and passes through the center of the circle. In other words, the diameter represents the furthest distance in the circle.
- The diameter will always be twice the radius. If you know the radius, you can multiply it by 2 to get the diameter; if you know the diameter, you can divide by 2 to get the radius.
- Remember that a line that joins two points on a circle (also known as a chord) but does not pass through the center of the circle is not a diameter; the line will have a shorter distance.
Step 4. Learn how to represent circles
A circle is generally defined by its center, so in mathematics, the symbol for a circle is a circle with a dot in the middle. To represent a circle at a specific location in the graph, just write the location of the center of the circle after the circle symbol.
The circle located at point 0 will look like this: O
Part 2 of 2: Drawing a Circle Graph
Step 1. Know the equation of the circle
The general form for the equation of a circle is (x – a)^2 + (y – b)^2 = r^2. The symbols a and b represent the center of the circle as a point on the axis, where a is the horizontal displacement, and b is the vertical displacement. The symbol r represents the radius.
For example, use the equation x^2 + y^2 = 16
Step 2. Find the center of your circle
Remember that the center of the circle is shown as a and b in the equation of the circle. If there are no parentheses – as in our example – it means that a = 0 and b = 0.
In our example, note that you can write (x – 0)^2 + (y – 0)^2 = 16. You can see that a = 0 and b = 0, and thus the center of your circle is at the origin., at the point (0, 0)
Step 3. Find the radius of the circle
Recall that r represents the radius. Be careful: if the r part of your equation doesn't have a square, you'll have to find your radius.
So, in our example, you have 16 for r, but no square. To find the radius, write r^2 = 16; then, you can solve it to see that the radius is 4. Now, you can write the equation as x^2 + y^2 =4^2
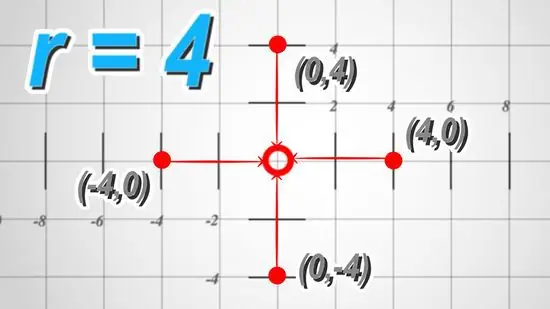
Step 4. Draw the points of your radius on the coordinate plane
For any number of radii you have, count the number in four directions from the center: left, right, up, and down.
In the example, you will count 4 in all directions to represent the points of the radius, because our radius is 4
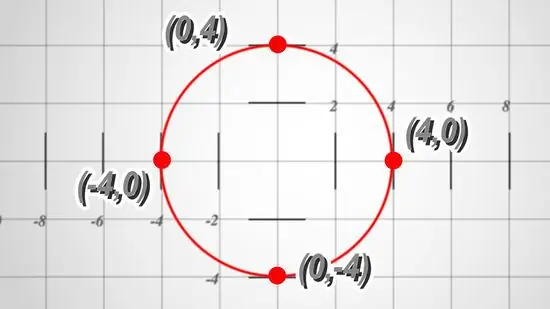
Step 5. Connect the dots
To draw a circle graph, connect the points using curved curves.
