- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-01-23 12:04.
Two fractions are equivalent if they have the same value. Knowing how to convert fractions to their equivalent forms is an extremely important math skill, required for all forms of mathematics from basic algebra to advanced calculus. This article will provide several ways to calculate equivalent fractions from basic multiplication and division to more complex ways of solving equivalent fractional equations.
Step
Method 1 of 5: Compiling Equivalent Fractions

Step 1. Multiply the numerator and denominator by the same number
Two different but equivalent fractions have, by definition, a numerator and denominator that are multiples of each other. In other words, multiplying the numerator and denominator of a fraction by the same number will produce equivalent fractions. Although the numbers in the new fraction will be different, the fractions will have the same value.
- For example, if we take the fraction 4/8 and multiply both the numerator and denominator by 2, we get (4×2)/(8×2) = 8/16. These two fractions are equivalent.
- (4×2)/(8×2) is actually the same as 4/8×2/2. Remember that when multiplying two fractions, we are multiplying straight, meaning the numerator by the numerator and the denominator by the denominator.
- Note that 2/2 equals 1 if you do the division. Thus, it is easier to understand why 4/8 and 8/16 are equivalent because multiplying 4/8 × (2/2) = remains 4/8. In the same way, it's the same as saying 4/8 = 8/16.
- Any given fraction has an infinite number of equivalent fractions. You can multiply both the numerator and denominator by any integer, regardless of size or small, to get an equivalent fraction.

Step 2. Divide the numerator and denominator by the same number
Like multiplication, division can also be used to find a new fraction that is equivalent to your original fraction. Just divide the numerator and denominator of a fraction by the same number to get the equivalent fraction. There is one drawback to this process-the final fraction must have integers in both the numerator and denominator to be true.
For example, let's look back at 4/8. If, instead of multiplying, we divide both the numerator and denominator by 2, we get (4 2)/(8 2) = 2/4. 2 and 4 are integers, so these equivalent fractions are true
Method 2 of 5: Using Basic Multiplication to Determine Equality

Step 1. Find the number that must be multiplied by the smaller denominator to get the larger denominator
Many problems about fractions involve determining if two fractions are equivalent. By calculating this number, you can begin to equate the fractional terms to determine equality.
- For example, reuse the fractions 4/8 and 8/16. The smaller denominator is 8 and we have to multiply the number by 2 to get the larger denominator, which is 16. So the number in this case is 2.
- For more difficult numbers, you can divide the larger denominator by the smaller denominator. In this case, 16 is divided by 8, which still yields 2.
- The number is not always an integer. For example, if the denominators are 2 and 7, then the number is 3, 5.

Step 2. Multiply the numerator and denominator of the fraction that has the smaller term by the number from the first step
Two different but equivalent fractions have, by definition, numerator and denominator which are multiples of each other. In other words, multiplying the numerator and denominator of a fraction by the same number will produce an equivalent fraction. Although the numbers in this new fraction will be different, these fractions will have the same value.
For example, if we use the fraction 4/8 from step one and multiply the numerator and denominator by the number we defined earlier, which is 2, we get (4×2)/(8×2) = 8/16. This result proves that these two fractions are equivalent.
Method 3 of 5: Using Basic Division to Determine Equality

Step 1. Count each fraction as a decimal number
For simple fractions without variables, you can represent each fraction as a decimal number to determine equality. Since every fraction is actually a division problem, this is the simplest way to determine equality.
- For example, use the fraction we used earlier, 4/8. The fraction 4/8 is equivalent to saying 4 divided by 8, which is 4/8 = 0.5. You can also solve the other example, which is 8/16 = 0.5. No matter the terms in a fraction, the fraction is equivalent if both numbers are the same when represented in decimal.
- Keep in mind that decimal expressions can have multiple digits before the equality is obvious. As a basic example, 1/3 = 0.333 repeats while 3/10 = 0.3. Using more than one digit, we see that these two fractions are not equivalent.

Step 2. Divide the numerator and denominator of a fraction by the same number to get an equivalent fraction
For more complex fractions, the division method requires additional steps. Whereas with multiplication, you can divide the numerator and denominator of a fraction by the same number to get an equivalent fraction. There is one drawback to this process. The final fraction must have integers in both the numerator and denominator to be true.
For example, let's look back at 4/8. If, instead of multiplying, we divide the numerator and denominator by 2, we get (4 2)/(8 2) = 2/4. 2 and 4 are integers, so these equivalent fractions are true.

Step 3. Simplify the fractions to their simplest terms
Most fractions are usually written in their simplest terms, and you can convert fractions to their simplest form by dividing by the greatest common factor (GCF). This step is done in the same logic as writing equivalent fractions, converting them to the same denominator, but this method attempts to simplify each fraction to its smallest possible terms.
- When a fraction is in its simplest form, the numerator and denominator have the smallest possible values. Both cannot be divided by any integer to get the smaller value. To convert a fraction that is not in its simplest form into its simplest equivalent form, we divide the numerator and denominator by their greatest common factor.
-
The greatest common factor (GCF) of the numerator and denominator is the largest number that divides them to give an integer result. So, in our 4/8 example, because
Step 4. is the largest number that is divisible by 4 and 8, we will divide the numerator and denominator of our fraction by 4 to get the simplest terms. (4 4)/(8 4) = 1/2. For our other example, 8/16, the GCF is 8, which also returns the value 1/2 as the simplest expression of a fraction.
Method 4 of 5: Using Cross Products to Find Variables

Step 1. Arrange the two fractions so that they are equal to each other
We use cross multiplication for math problems where we know the fractions are equivalent, but one of the numbers has been replaced by a variable (usually x) that we have to solve. In cases like this, we know that these fractions are equivalent because they are the only terms on the other side of the equals sign, but often the way to find the variable is not obvious. Fortunately, with cross multiplication, solving these types of problems is easy.

Step 2. Take two equivalent fractions and multiply them by an "X" shape
In other words, you multiply the numerator of one fraction by the denominator of another fraction and vice versa, then arrange the two answers to match each other and solve.
Take our two examples, 4/8 and 8/16. Neither has a variable, but we can prove the concept because we already know that they are equivalent. By cross multiplying, we get 4/16 = 8 x 8, or 64 = 64, which is true. If these two numbers are not equal, then the fractions are not equivalent

Step 3. Add variables
Since cross multiplication is the easiest way to find equivalent fractions when you have to find variables, let's add variables.
-
For example, let's use the equation 2/x = 10/13. To cross multiply, we multiply 2 by 13 and 10 by x, then set our answers equal to each other:
- 2 × 13 = 26
- 10 × x = 10x
- 10x = 26. From here, finding the answer to our variable is a simple algebra problem. x = 26/10 = 2, 6, making the initial equivalent fraction 2/2, 6 = 10/13.

Step 4. Use cross multiplication for multiple-variable fractions or variable expressions
One of the best things about cross multiplication is that it actually works the same way, whether you're working with two simple fractions (as above) or more complex fractions. For example, if both fractions have variables, you only need to eliminate these variables in the solving process. Similarly, if your fraction's numerator or denominator has a variable expression (like x + 1), just "multiply" it using the distributive property and solve as usual.
-
For example, let's use the equation ((x + 3)/2) = ((x + 1)/4). In this case, as above, we'll solve it by cross product:
- (x + 3) × 4 = 4x + 12
- (x + 1) × 2 = 2x + 2
- 2x + 2 = 4x + 12, then we can simplify the fraction by subtracting 2x from both sides
- 2 = 2x + 12, then we isolate the variable by subtracting 12 from both sides
- -10 = 2x, and divide by 2 to find x
- -5 = x
Method 5 of 5: Using Quadratic Formulas to Find Variables
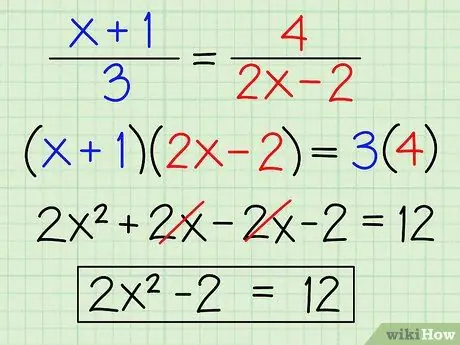
Step 1. Cross the two fractions
For equality problems that require a quadratic formula, we still start by using cross product. However, any cross product that involves multiplying the terms of a variable by the terms of another variable is likely to result in an expression that cannot be easily solved using algebra. In cases like these, you may need to use techniques such as factoring and/or quadratic formulas.
-
For example, let's look at the equation ((x +1)/3) = (4/(2x - 2)). First, let's cross multiply:
- (x + 1) × (2x - 2) = 2x2 + 2x -2x - 2 = 2x2 - 2
- 4 × 3 = 12
- 2x2 - 2 = 12.
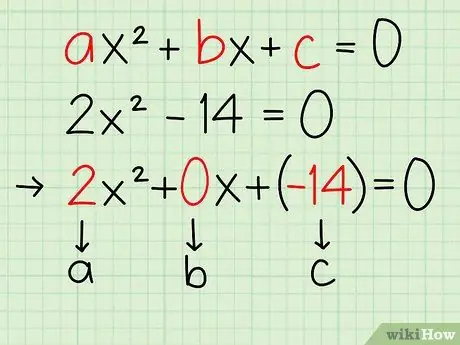
Step 2. Write the equation as a quadratic equation
In this section, we want to write this equation in quadratic form (ax2 + bx + c = 0), which we do by setting the equation equal to zero. In this case, we subtract 12 from both sides to get 2x2 - 14 = 0.
Some values may be equal to 0. Even though 2x2 - 14 = 0 is the simplest form of our equation, the real quadratic equation is 2x2 + 0x + (-14) = 0. It may be helpful at the outset to write down the form of the quadratic equation even if some values are equal to 0.
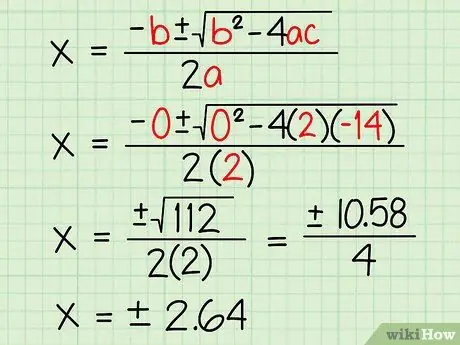
Step 3. Solve by plugging the numbers from your quadratic equation into the quadratic formula
Quadratic formula (x = (-b +/- (b2 - 4ac))/2a) will help us to find our x value in this section. Don't be afraid of the length of the formula. You just take the values from your quadratic equation in step two and put them in the right places before solving them.
- x = (-b +/- (b2 - 4ac))/2a. In our equation, 2x2 - 14 = 0, a = 2, b = 0, and c = -14.
- x = (-0 +/- (02 - 4(2)(-14)))/2(2)
- x = (+/- (0 - -112))/2(2)
- x = (+/- (112))/2(2)
- x = (+/- 10.58/4)
- x = +/- 2, 64

Step 4. Check your answer by re-entering the value of x into your quadratic equation
By plugging the calculated x value back into your quadratic equation from step two, you can easily determine if you got the answer right. In this example, you'll plug 2, 64 and -2, 64 into the original quadratic equation.
Tips
- Converting a fraction to its equivalent is actually a form of multiplying a fraction by 1. In converting 1/2 to 2/4, multiplying the numerator and denominator by 2 is the same as multiplying 1/2 by 2/2, which equals 1.
-
If desired, convert the mixed number to a common fraction to make the conversion easier. Of course, not all of the fractions you come across will be as easy as converting our 4/8 example above. For example, mixed numbers (such as 1 3/4, 2 5/8, 5 2/3, etc.) can make the conversion process a bit more complicated. If you have to convert a mixed number to a common fraction, you can do this in two ways: by converting the mixed number to a common fraction, then converting it as usual, or by maintaining the form of mixed numbers and getting answers in the form of mixed numbers.
- To convert to a common fraction, multiply the integer component of the mixed number by the denominator of the fractional component and then add to the numerator. For example, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Then, if desired, you can change it as needed. For example, 5/3 × 2/2 = 10/6, which remains equal to 1 2/3.
- However, we don't have to convert it to a common fraction as above. Otherwise, we leave the integer component alone, change only the fractional component, and add the integer component unchanged. For example, for 3 4/16, we only see 4/16. 4/16 4/4 = 1/4. So, by adding our integer components back, we get a new mixed number, 3 1/4.
Warning
- Multiplication and division can be used to get equivalent fractions because multiplication and division with the fractional form of the number 1 (2/2, 3/3, etc.) gives an answer that is equivalent to the original fraction, by definition. Addition and subtraction cannot be used.
-
Even though you multiply the numerators and denominators when you multiply fractions, you don't add or subtract the denominators when you add or subtract fractions.
For example, above, we know that 4/8 4/4 = 1/2. If we add up by 4/4, we get a completely different answer. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 or 3/2, they are not equal to 4/8.






