How to Find the Number of Terms in an Arithmetic Series: 3 Steps

Table of contents:

How to Find the Number of Terms in an Arithmetic Series: 3 Steps
How to Find the Number of Terms in an Arithmetic Series: 3 Steps

Video: How to Find the Number of Terms in an Arithmetic Series: 3 Steps

Video: How to Find the Number of Terms in an Arithmetic Series: 3 Steps
Video: Wave Period and Frequency 2024, May
Anonim

Finding the number of terms in an arithmetic series may sound daunting, but it's actually quite simple. You just need to enter the numbers into the formula U = a + (n - 1) b and find the value of n, which is the number of terms. Know that U is the last number in the series, a is the first term in the series, and b is the difference or difference between adjacent terms.

Step

Find a Number of Terms in an Arithmetic Sequence Step 1
Find a Number of Terms in an Arithmetic Sequence Step 1

Step 1. Identify the first, second, and last terms in the series

Usually, questions like this give the first 3 or more terms, and the last term.

For example, your question looks like this: 107, 101, 95…-61. In this case, the first term is 107 and the last term is -61. You need all this information to solve the problem

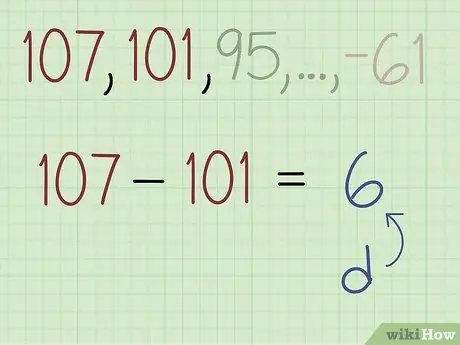
Find a Number of Terms in an Arithmetic Sequence Step 2
Find a Number of Terms in an Arithmetic Sequence Step 2

Step 2. Subtract the second term from the first term to find the difference (b)

In the example problem, the first term is 107 and the second term is 101. To find the difference, subtract 101 by 107 and get -6.

Find a Number of Terms in an Arithmetic Sequence Step 3
Find a Number of Terms in an Arithmetic Sequence Step 3

Step 3. Use the formula U = a + (n - 1) b to find n.

Enter the last term (U ), the first term (a), and the difference (b). Count the equations until you get the value of n.

For our example problem, write: -61 = 107 + (n - 1) -6. Subtract 107 from both sides so that only -168 = (n - 1) -6 remains. Then, divide both sides by -6 to get 28 = n - 1. Solve by adding 1 to both sides so n = 29

Tips

The difference between the first and last terms will always be divisible by difference

Recommended:

How to Find a Phone Number: 6 Steps (with Pictures)

How to Find a Phone Number: 6 Steps (with Pictures)

Now, many people are starting to leave their landlines and switch to cell phones. Since the phone book doesn't include cell phone numbers, you'll have a little trouble contacting people you don't know. Knowing how to find a cell phone number will help you call a specific person at an important time, reconnect with an old friend, or connect with someone who gave you their cell phone number in the past.

How to Find Model Number on HP Laptop: 10 Steps

How to Find Model Number on HP Laptop: 10 Steps

This wikiHow teaches you how to find the model number of an HP laptop. You can use this number to identify a specific device when someone else has the laptop repaired, or to make sure certain hardware (eg batteries) is compatible with the laptop.

How to Understand Terms in the Stock World: 14 Steps (with Pictures)

How to Understand Terms in the Stock World: 14 Steps (with Pictures)

If you're starting to have an interest in stock trading, you've probably already decided on a company or two to study. In general, any company whose shares can be traded can be investigated and analyzed in terms of their shares. These terms are a kind of brief description of the shares of these companies, and from this we can determine the performance of these companies on the stock market.

How to Find the Sum of an Arithmetic Series: 10 Steps (with Pictures)

How to Find the Sum of an Arithmetic Series: 10 Steps (with Pictures)

An arithmetic series is a series of numbers in which each term increases by a constant amount. To add up the numbers in an arithmetic series, you simply add up each number. However, when the number of numbers in the series is too large, this method becomes impractical.

4 Ways to Find Terms in an Arithmetic Sequence

4 Ways to Find Terms in an Arithmetic Sequence

An arithmetic series is a series of numbers in which the difference between one number and the number next to it is always the same. For example, the series of even numbers 0, 2, 4, 6, 8{displaystyle 0, 2, 4, 6, 8} … adalah deret aritmetika karena selisih satu angka dengan angka berikutnya selalu 2.