Integers are the set of natural numbers, their negative numbers, and zero. However, some integers are natural numbers, including 1, 2, 3, and so on. The negative values are, -1, -2, -3, and so on. So, integers are the set of numbers including (…-3, -2, -1, 0, 1, 2, 3, …). Integers are never fractions, decimals, or percentages; Integers can only be whole numbers. To solve integers and use their properties, learn to use addition and subtraction properties and use multiplication properties.
Step
Method 1 of 2: Using Addition and Subtraction Properties
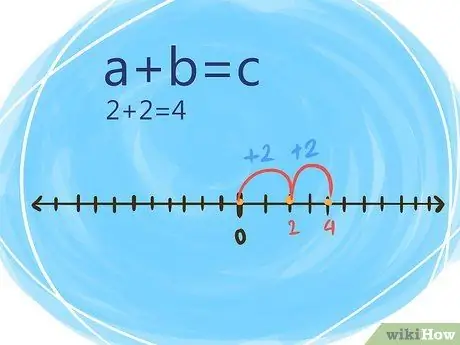
Step 1. Use the commutative property when both numbers are positive
The commutative property of addition states that changing the order of numbers does not affect the sum of the equations. Do the sum as follows:
- a + b = c (where a and b are positive, the sum of c is also positive)
- For example: 2 + 2 = 4
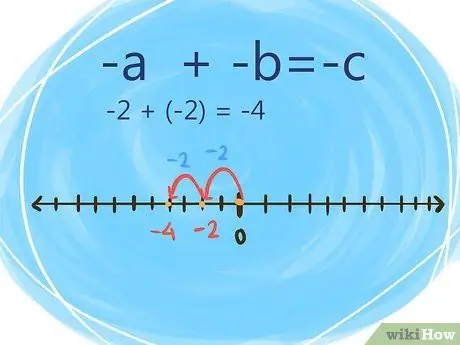
Step 2. Use the commutative property if a and b are negative
Do the sum as follows:
- -a + -b = -c (where a and b are negative, you'll find the absolute value of the numbers, then you continue to add up the numbers, and use the negative sign for the sum)
- For example: -2+ (-2)=-4
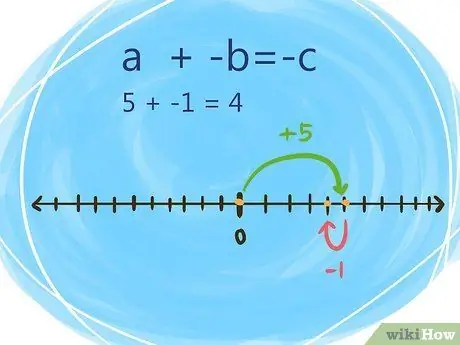
Step 3. Use the commutative property when one number is positive and the other is negative
Do the sum as follows:
- a + (-b) = c (when your terms have different signs, determine the value of the larger number, then find the absolute value of both terms and subtract the smaller value from the larger value. Use the sign of the larger number bigger for the answer.)
- For example: 5 + (-1) = 4
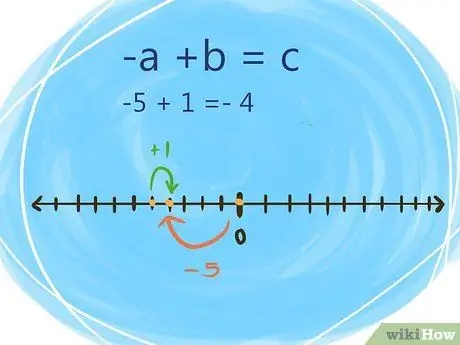
Step 4. Use the commutative property when a is negative and b is positive
Do the sum as follows:
- -a +b = c (find the absolute value of the numbers, and again, continue to subtract the smaller value from the larger value and use the sign of the larger value)
- For example: -5 + 2 = -3
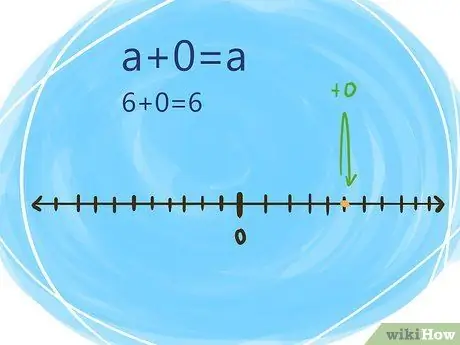
Step 5. Understand the identity of addition when adding numbers with zeros
The sum of any number when added to zero is the number itself.
- An example of a sum identity is: a + 0 = a
- Mathematically, the addition identity looks like: 2 + 0 = 2 or 6 + 0 = 6
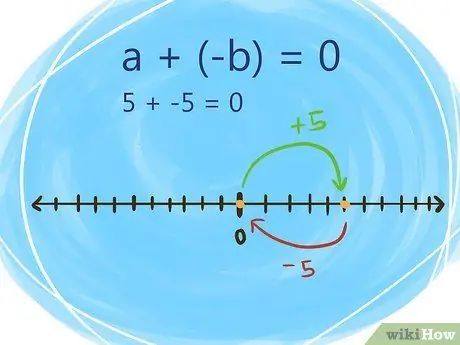
Step 6. Know that adding the inverse of addition results in zero
When you add the addition inverse of a number, the result is zero.
- The inverse of addition is when a number is added to a negative number that is equal to the number itself.
- For example: a + (-b) = 0, where b is equal to a
- Mathematically, the inverse of addition looks like: 5 + -5 = 0
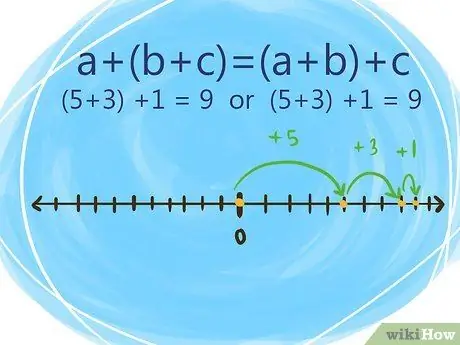
Step 7. Realize that the associative property states that regrouping added numbers does not change the sum of the equations
The order in which you add numbers doesn't affect the result.
For example: (5+3) +1 = 9 has the same sum as 5+ (3+1) = 9
Method 2 of 2: Using the Multiplication Properties
Step 1. Realize that the associative property of multiplication means that the order in which you multiply does not affect the product of the equation
Multiplying a*b = c is also the same as multiplying b*a = c. However, the sign of the product can change depending on the signs of the original numbers:
-
If a and b have the same sign, then the sign of the product is positive. For example:
Solve Integers and Their Properties Step 8Bullet1 - When a and b are positive numbers and not equal to zero: +a * +b = +c
- When a and b are negative numbers and not equal to zero: -a * -b = +c
-
If a and b have different signs, then the sign of the product is negative. For example:
-
When a is positive and b is negative: +a * -b = -c
Solve Integers and Their Properties Step 8Bullet2
-
- However, understand that any number multiplied by zero equals zero.
Step 2. Understand that the multiplication identity of integers states that any integer multiplied by 1 equals the integer itself
Unless the integer is zero, any number multiplied by 1 is the number itself.
- For example: a*1 = a
Solve Integers and Their Properties Step 9Bullet1 -
Remember, any number multiplied by zero equals zero.
Solve Integers and Their Properties Step 9Bullet2
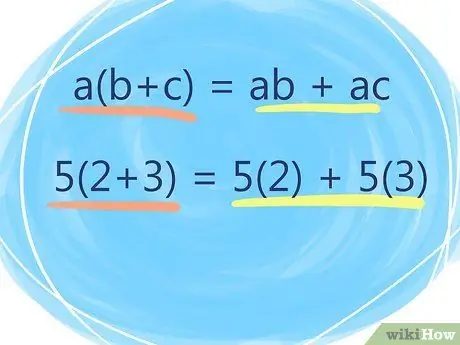
Step 3. Recognize the distributive property of multiplication
The distributive property of multiplication says that any number "a" multiplied by the sum of "b" and "c" in parentheses is the same as "a" times "c" plus "a" times "b".
- For example: a(b+c) = ab + ac
- Mathematically, this property looks like: 5(2+3) = 5(2) + 5(3)
- Note that there is no inverse property for multiplication because the inverse of whole numbers is a fraction, and fractions are not elements of whole numbers.
