- Author Jason Gerald [email protected].
- Public 2024-01-15 08:07.
- Last modified 2025-06-01 06:05.
The root symbol (√) represents the square root of a number. You can find the root symbol in algebra or even in carpentry or any other field that involves geometry or calculating relative sizes or distances. If the roots don't have the same index, you can change the equation until the indices are the same. If you want to know how to multiply roots with or without coefficients, just follow these steps.
Step
Method 1 of 3: Multiplying Roots Without Coefficients
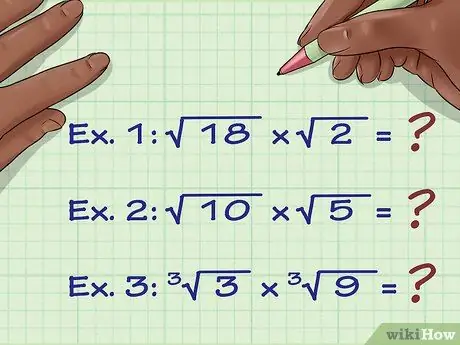
Step 1. Make sure the roots have the same index
To multiply roots using the basic method, these roots must have the same index. "Index" is a very small number, written at the top left of the line in the root symbol. If there is no index number, the root is the square root (index 2) and can be multiplied by any other square root. You can multiply the roots by a different index, but this method is more complicated and will be explained later. Here are two examples of multiplication using roots with the same index:
- Example 1: (18) x (2) = ?
- Example 2: (10) x (5) = ?
- Example 3: 3(3) x 3√(9) = ?

Step 2. Multiply the numbers under the square root
Next, just multiply the numbers that are under the square root or sign and place it under the square root sign. Here's how you do it:
- Example 1: (18) x (2) = (36)
- Example 2: (10) x (5) = (50)
- Example 3: 3(3) x 3√(9) = 3√(27)

Step 3. Simplify the root expression
If you multiply the roots, it is possible that the result can be simplified to a perfect square or perfect cubic, or that the result can be simplified by finding the perfect square that is a factor of the product. Here's how you do it:
- Example 1: (36) = 6. 36 is a perfect square because it is the product of 6 x 6. The square root of 36 is only 6.
-
Example 2: (50) = (25 x 2) = ([5 x 5] x 2) = 5√(2). Although 50 is not a perfect square, 25 is a factor of 50 (because it divides 50 evenly) and is a perfect square. You can break 25 into its factors, 5 x 5, and take one 5 out of the square root sign to simplify the expression.
You can think of it this way: If you put 5 back under the root, it multiplies itself and returns to 25
- Example 3:3(27) = 3. 27 is a perfect cubic because it is the product of 3 x 3 x 3. Thus, the cubic root of 27 is 3.
Method 2 of 3: Multiplying Roots By Coefficients

Step 1. Multiply the coefficients
Coefficients are numbers that are outside the root. If no coefficient number is listed, then the coefficient is 1. Multiply the coefficient. Here's how you do it:
-
Example 1: 3√(2) x (10) = 3√(?)
3 x 1 = 3
-
Example 2: 4√(3) x 3√(6) = 12√(?)
4 x 3 = 12
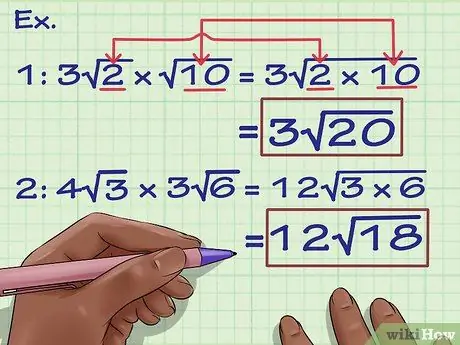
Step 2. Multiply the numbers in the root
Once you've multiplied the coefficients, you can multiply the numbers in the roots. Here's how you do it:
- Example 1: 3√(2) x (10) = 3√(2 x 10) = 3√(20)
- Example 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)

Step 3. Simplify the product
Next, simplify the numbers under the roots by finding perfect squares or multiples of the numbers under the roots that are perfect squares. Once you've simplified the terms, just multiply them by the coefficients. Here's how you do it:
- 3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)
- 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)
Method 3 of 3: Multiplying Roots By Different Indices
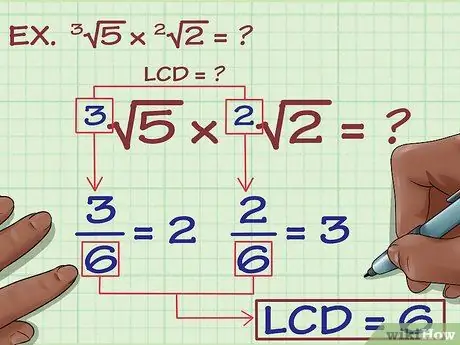
Step 1. Find the LCM (smallest multiple) of the index
To find the LCM of the index, find the smallest number that is divisible by both indexes. Find the LCM of the index of the following equation:3(5) x 2√(2) = ?
The indices are 3 and 2. 6 is the LCM of these two numbers because 6 is the smallest number that is divisible by both 3 and 2. 6/3 = 2 and 6/2 = 3. To multiply the roots, both indices must be converted to 6

Step 2. Write down each expression with the new LCM as its index
Here's the expression in the equation with the new index:
6(5) x 6√(2) = ?
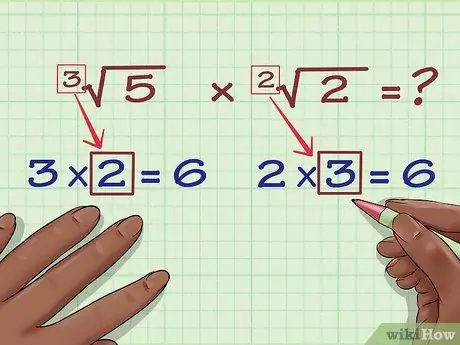
Step 3. Find the number you should use to multiply each original index to find its LCM
For expression 3(5), you need to multiply index 3 by 2 to get 6. For the expression 2(2), you need to multiply index 2 by 3 to get 6.
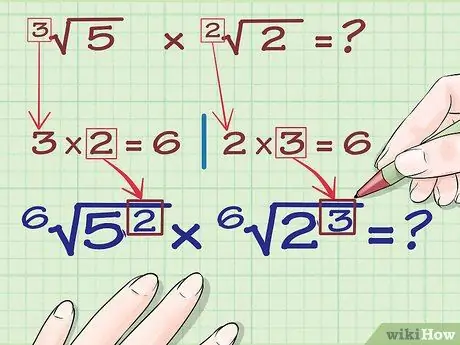
Step 4. Make this number the exponent of the number inside the root
For the first equation, make the number 2 as the exponent of number 5. For the second equation, make the number 3 as the exponent of number 2. Here's the equation:
- 2 6√(5) = 6√(5)2
- 3 6√(2) = 6√(2)3
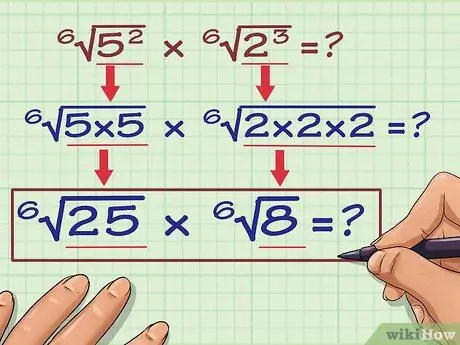
Step 5. Multiply the numbers in the root by the exponent
Here's how you do it:
- 6√(5)2 = 6(5 x 5) = 6√25
- 6√(2)3 = 6(2 x 2 x 2) = 6√8
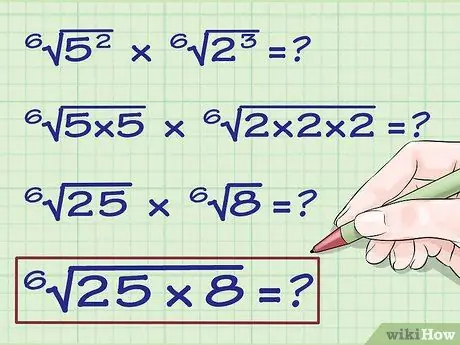
Step 6. Put these numbers under one root
Put the numbers under one root and connect them with a multiplication sign. Here is the result: 6(8 x 25)
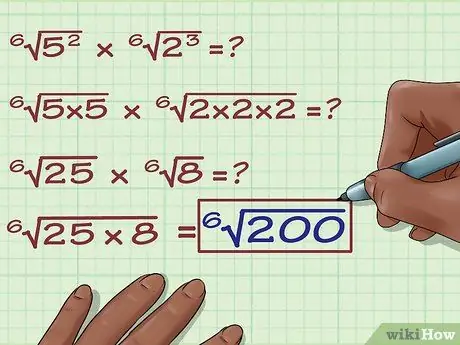
Step 7. Multiply
6(8 x 25) = 6(200). This is the final answer. In some cases, you can simplify this expression - for example, you can simplify this equation if you find a number that can be multiplied by itself 6 times and is a factor of 200. But in this case, the expression can't be simplified any further.
Tips
- If a "coefficient" is separated from the root sign by a plus or minus sign, it's not a coefficient - it's a separate term and must be worked out separately from the root. If a root and another term are in the same parentheses - for example (2 + (root)5), you must calculate 2 and (root)5 separately when performing operations inside brackets, but when performing operations outside of brackets, you must calculate (2 + (root)5) as a unit.
- The "coefficient" is the number, if any, that is placed immediately before the square root. So for example, in the expression 2(root)5, 5 is under the sign of the root and the number 2 is outside the root, which is the coefficient. When a root and a coefficient are put together, it means the same as multiplying the root by the coefficient, or to continue the example to 2 * (root)5.
- The root sign is another way of expressing the exponent of a fraction. In other words, the square root of any number equals that number to the power of 1/2, the cubic root of any number equals that number to the power of 1/3, and so on.






