- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
The square root of a number is easy to find if the answer is an integer. If the answer is not an integer, there is a series of processes you can follow to get the square root, even if you don't use a calculator. For that you need to understand the basics of multiplication, addition, and division.
Step
Method 1 of 3: Finding the Square Root of an Integer
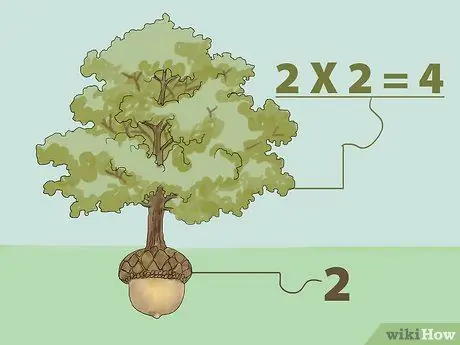
Step 1. Find the perfect square root by multiplying
The square root of a number is a number which when multiplied by itself returns the original number. In other words: "What number can we multiply by itself to get the number we want?"
- For example, the square root of 1 is 1 because 1 multiplied by 1 is 1 (1X1=1). Thus, the square root of 4 is 2 because 2 multiplied by 2 is 4 (2X2=4). Think of the square root concept as a tree. A tree grows from seed. So, a tree is bigger than a seed, which grows from the seed that is the root. From the example above, 4 is the tree, and 2 is the seed.
- So, the square root of 9 is 3 (3X3=9), of 16 is 4 (4X4=16), of 25 is 5 (5X5=25), of 36 is 6 (6X6=36), of 49 is 7 (7X7 =49), from 64 is 8 (8X8=64), from 81 is 9 (9X9=81), and from 100 is 10 (10X10=100).
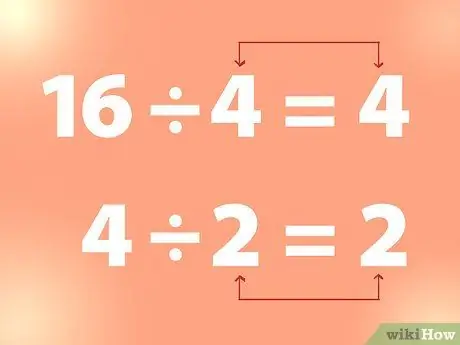
Step 2. Use continuous division to find the square root
To find the square root of an integer, you can divide the integer by a number until you get a number that equals the divisor.
- Example: 16 divided by 4 is 4. And 4 divided by 2 is 2, and so on. Thus, from the above example, 4 is the square root of 16 and 2 is the square root of 4.
- Perfect square roots have no fractions or decimals because they are whole numbers.
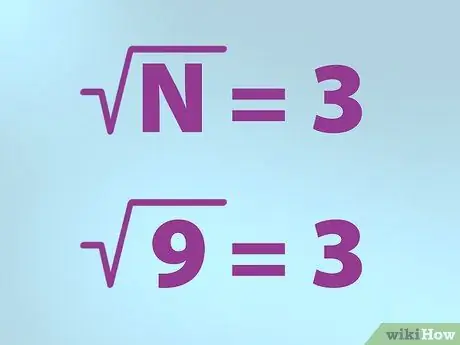
Step 3. Use the correct symbol for the square root
Mathematicians use a special symbol to represent the square root. The shape is like a check mark with plus a line at the top right.
- N equals the number for which you want to find the square root. N is placed under the check mark.
- So, if you want to find the square root of 9, write a formula by putting "N" (9) inside a check mark (symbol "root") then write an equal sign and followed by 3. It means "square root of 9 is equal to 3".
Method 2 of 3: Finding the Square Root of Another Number
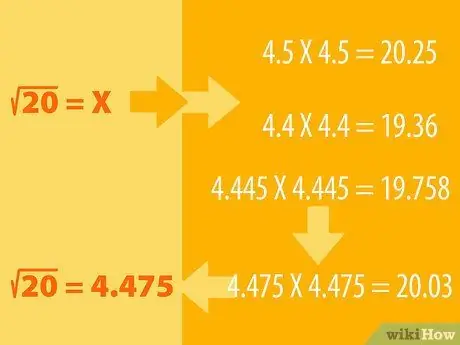
Step 1. Guess, and do the process of elimination
It is difficult to find the square root of a non-integer number. However, that doesn't mean it's impossible.
- For example, say you want to find the square root of 20. We know that 16 is a perfect square whose square root is 4 (4X4=16). Then the 25 square roots are 5 (5X5=25), so the square root of 20 must lie between them.
- You can guess that the square root of 20 is 4.5. Now square 4.5 to see the result. That is, we multiply 4, 5 by itself: 4, 5X4, 5. See if the answer is more or less than 20. If your guess is too far, try another number (eg 4, 6 or 4, 4) and adjust the guess accordingly. you until you get the number 20.
- For example, 4, 5X4, 5 = 20, 25, so logically we have to find a smaller number, maybe 4, 4. 4, 4X4, 4 = 19, 36. So, the square root of 20 must lie between 4, 5 and 4, 4. Try with 4, 445X4, 445. The result is 19, 758. The result is getting closer. Keep trying with other numbers until you get 4, 475X4, 475 = 20, 03. Rounded up, that number equals 20.

Step 2. Use the averaging process
This process also begins by finding the two nearest perfect squares that are flanked by the number.
- Then divide that number by one of the perfect square roots. Take the answer, then find the average between that number and the number you want to find the root of (you can find the average by adding the two together and dividing by two). Then divide the initial number by the average obtained. The last step, find the average of the results with the average calculated the first time.
- Sound complicated? It would be easier if given an example. For example, 10 lies between the two perfect squares 9 (3X3=9) and 16 (4X4=16). The square roots of both numbers are 3 and 4. So, divide 10 by the first number, 3. The result is 3, 33. Now find the average of 3 and 3, 33 by adding them together and dividing by 2. The result is 3, 1667 Now divide 10 by 3.1667. The result is 3.1579. Then find the average of 3.1579 and 3.1667 by adding them up and dividing by 2. The result is 3.1623.
- Check your result by multiplying the answer (in this example 3, 1623) by itself. The result of 3.1623 multiplied by 3.1623 turns out to be 10.001.
Method 3 of 3: Squaring Negative Numbers
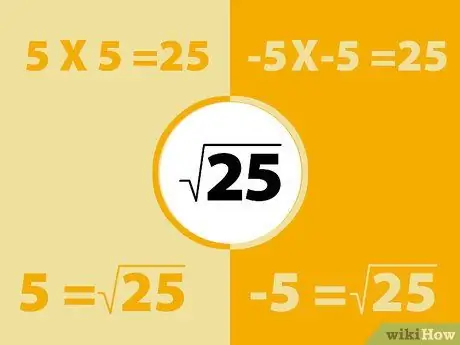
Step 1. Square negative numbers using the same method
Remember that negative multiplied by negative is positive. So, the square of a negative number will produce a positive number.
- For example, -5X-5 = 25. However, also remember that 5x5=25. So, the square root of 25 can be -5 or 5. Basically every number has two square roots.
- Similarly, 3X3=9 and -3X-3=9, so the square roots of 9 are 3 and -3. The positive square root is called the "principal root". At this point, we just need to pay attention to this answer.

Step 2. Use a calculator
While it's best to be able to do the math by hand, there are many online calculators available for calculating square roots.
- Look for the square root button on a regular calculator.
- In the online calculator, directly enter the number for which you want to find the square root value and click the button. The computer will show you the square root value.
Tips
-
Always keep a few important perfect squares in mind:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Also remember this perfect square: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Also note this: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






