- Author Jason Gerald [email protected].
- Public 2023-12-16 10:50.
- Last modified 2025-01-23 12:04.
A polynomial is a mathematical structure with a set of terms consisting of number constants and variables. There are certain ways, in which polynomials must be multiplied based on the number of terms contained in each polynomial. Here's what you need to know about multiplying polynomials.
Step
Method 1 of 5: Multiplying Two Mononomials

Step 1. Check the problem
Problems involving two monomials will only involve multiplication. There will be no addition or subtraction.
- A polynomial problem involving two monomials or two single-term polynomials, will look like: (ax) * (by); or (ax) * (bx)'
- Example: 2x * 3y
-
Example: 2x * 3x
Note that a and b represent constants or the digits of a number, while x and y represent variables

Step 2. Multiply the constants
Constants refer to the number digits in the problem. These constants are multiplied as usual according to the standard multiplication table.
- In other words, in this part of the problem, you are multiplying a and b.
- Example: 2x * 3y = (6)(x)(y)
- Example: 2x * 3x = (6)(x)(x)
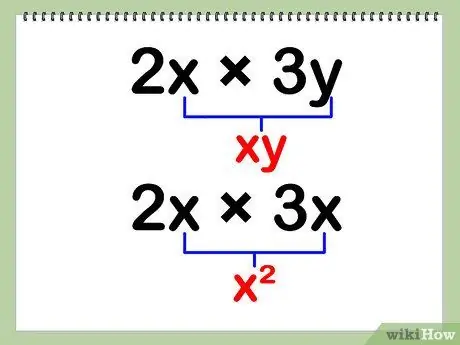
Step 3. Multiply the variables
Variables refer to the letters in the equation. When you multiply these variables, the different variables only need to be combined, while the similar variables will be squared.
- Note that when you multiply a variable by a similar variable, you increase the power of that variable by one.
- In other words, you're multiplying x and y or x and x.
- Example: 2x * 3y = (6)(x)(y) = 6xy
- Example: 2x * 3x = (6)(x)(x) = 6x^2
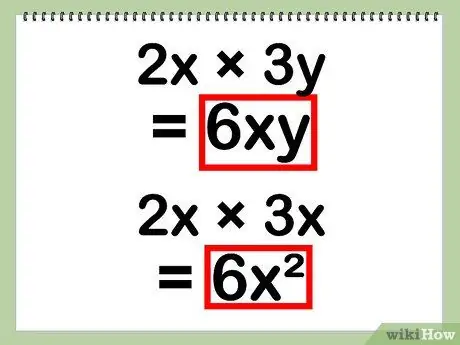
Step 4. Write down your final answer
Because of the simplified nature of the problem, you won't have like terms that you need to combine.
- Result of (ax) * (by) together with abxy. Almost the same, the result of (ax) * (bx) together with abx^2.
- Example: 6xy
- Example: 6x^2
Method 2 of 5: Multiplying Mononomials and Binomials
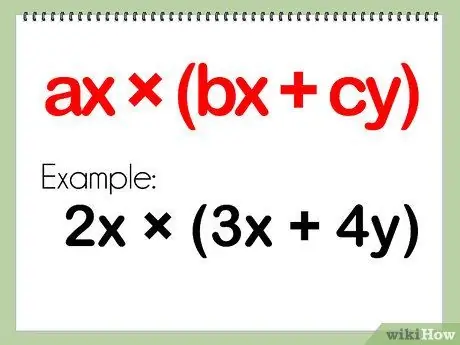
Step 1. Check the problem
Problems involving monomials and binomials will involve a polynomial that has only one term. The second polynomial will have two terms, which will be separated by a plus or minus sign.
- A polynomial problem involving monomials and binomials would look like: (ax) * (bx + cy)
- Example: (2x)(3x + 4y)
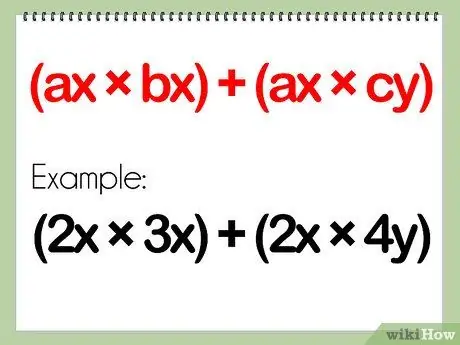
Step 2. Distribute the monomial to both terms in the binomial
Rewrite the problem so that all terms are separate, distributing the single-term polynomial to both terms in the two-term polynomial.
- After this step, the new rewrite form should look like this: (ax * bx) + (ax * cy)
- Example: (2x)(3x + 4y) = (2x)(3x) + (2x)(4y)
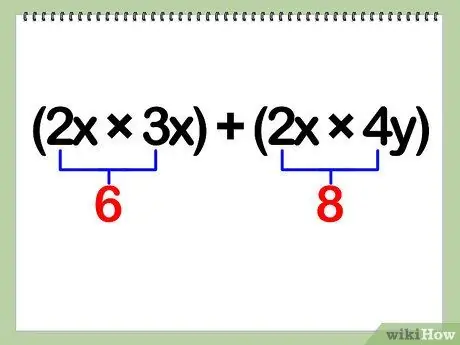
Step 3. Multiply the constants
Constants refer to the number digits in the problem. These constants are multiplied as usual according to the standard multiplication table.
- In other words, in this part of the problem, you are multiplying a, b, and c.
- Example: (2x)(3x + 4y) = (2x)(3x) + (2x)(4y) = 6(x)(x) + 8(x)(y)
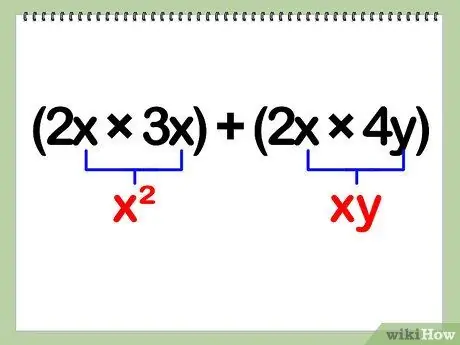
Step 4. Multiply the variables
Variables refer to the letters in the equation. When you multiply these variables, the different variables only need to be combined, while the similar variables will be squared.
- In other words, you're multiplying the x and y parts of the equation.
- Example: (2x)(3x + 4y) = (2x)(3x) + (2x)(4y) = 6(x)(x) + 8(x)(y) = 6x^2 + 8xy

Step 5. Write down your final answer
This type of polynomial problem is also simple enough that there is usually no need to combine like terms.
- The result will look like: abx^2 + acxy
- Example: 6x^2 + 8xy
Method 3 of 5: Multiplying Two Binomials
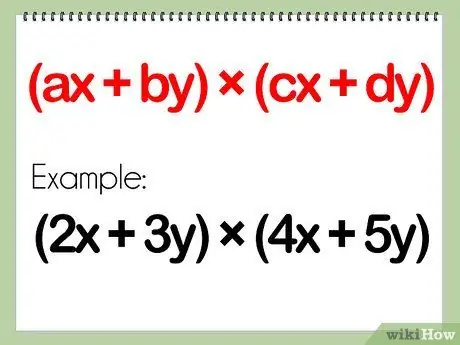
Step 1. Check the problem
Problems involving two binomials will involve two polynomials, each with two terms separated by a plus or minus sign.
- A polynomial problem involving two binomials would look like: (ax + by) * (cx + dy)
- Example: (2x + 3y)(4x + 5y)
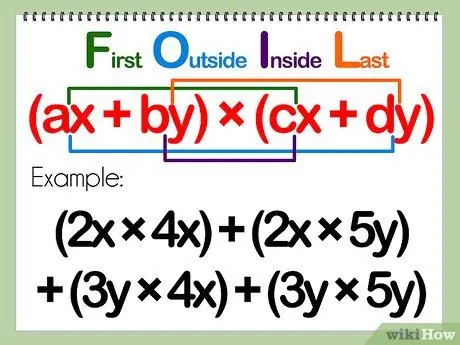
Step 2. Use PLDT to properly distribute the terms
PLDT is an acronym used to describe how to distribute tribes. Distribute the tribes pfirst, the tribes loutside, tribes dnature, and tribes tend.
- After that, your rewritten polynomial problem will effectively look like: (ax)(cx) + (ax)(dy) + (by)(cx) + (by)(dy)
- Example: (2x + 3y)(4x + 5y) = (2x)(4x) + (2x)(5y) + (3y)(4x) + (3y)(5y)
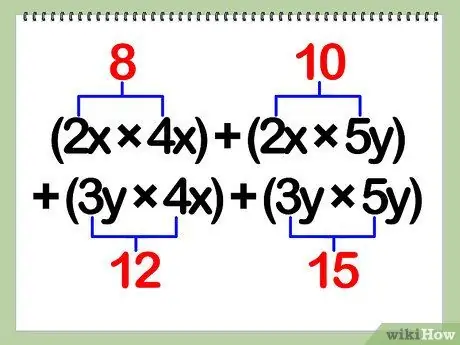
Step 3. Multiply the constants
Constants refer to the number digits in the problem. These constants are multiplied as usual according to the standard multiplication table.
- In other words, in this part of the problem, you are multiplying a, b, c, and d.
- Example: (2x)(4x) + (2x)(5y) + (3y)(4x) + (3y)(5y) = 8(x)(x) + 10(x)(y) + 12(y) (x) + 15(y)(y)

Step 4. Multiply the variables
Variables refer to the letters in the equation. When you multiply these variables, the different variables just need to be combined. However, when you multiply a variable by a similar variable, you increase the power of that variable by one.
- In other words, you're multiplying the x and y parts of the equation.
- Example: 8(x)(x) + 10(x)(y) + 12(y)(x) + 15(y)(y) = 8x^2 + 10xy + 12xy + 15y^2

Step 5. Combine any like terms and write down your final answer
This type of question is quite complicated so that it can produce like terms, meaning two or more final terms that have the same final variable. If this is the case, you will need to add or subtract like terms as needed, to determine your final answer.
- The result will look like: acx^2 + adxy + bcxy + bdy^2 = acx^2 + abcdxy + bdy^2
- Example: 8x^2 + 22xy + 15y^2
Method 4 of 5: Multiplying Mononomials and Three-Term Polynomials
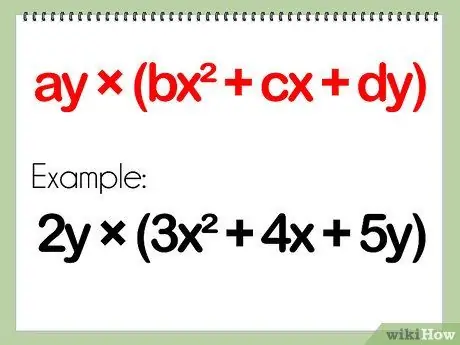
Step 1. Check the problem
Problems involving monomials and polynomials with three terms will involve a polynomial that has only one term. The second polynomial will have three terms, which will be separated by a plus or minus sign.
- A polynomial problem involving monomials and three-term polynomials would look like: (ay) * (bx^2 + cx + dy)
- Example: (2y)(3x^2 + 4x + 5y)
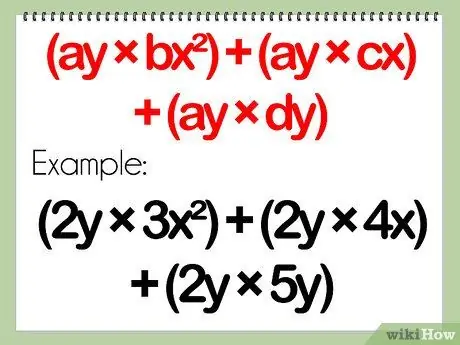
Step 2. Distribute the monomial to the three terms in the polynomial
Rewrite the problem so that all terms are separate, distributing the single-term polynomial over all three terms in the three-term polynomial.
- Rewritten, the new equation should look pretty much the same as: (ay)(bx^2) + (ay)(cx) + (ay)(dy)
- Example: (2y)(3x^2 + 4x + 5y) = (2y)(3x^2) + (2y)(4x) + (2y)(5y)
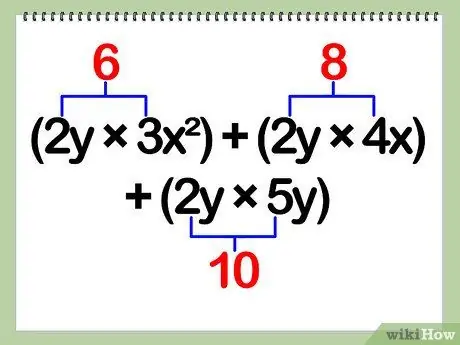
Step 3. Multiply the constants
Constants refer to the number digits in the problem. These constants are multiplied as usual according to the standard multiplication table.
- Again, for this step, you're multiplying a, b, c, and d.
- Example: (2y)(3x^2) + (2y)(4x) + (2y)(5y) = 6(y)(x^2) + 8(y)(x) + 10(y)(y)

Step 4. Multiply the variables
Variables refer to the letters in the equation. When you multiply these variables, the different variables just need to be combined. However, when you multiply a variable by a similar variable, you increase the power of that variable by one.
- So, multiply the x and y parts of the equation.
- Example: 6(y)(x^2) + 8(y)(x) + 10(y)(y) = 6yx^2 + 8xy + 10y^2
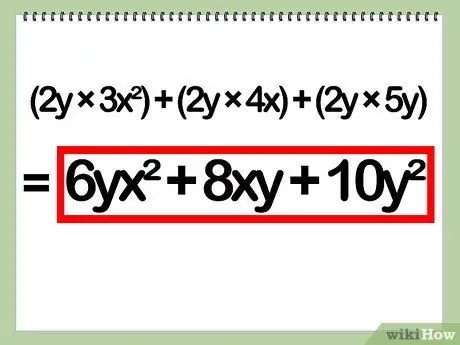
Step 5. Write down your final answer
Because the monomial is single-term at the beginning of this equation, you don't need to combine like terms.
- Once done, the final answer is: abyx^2 + acxy + ady^2
- Example of substitution of example values for constants: 6yx^2 + 8xy + 10y^2
Method 5 of 5: Multiplying Two Polynomials

Step 1. Check the problem
Each has two three-term polynomials with a plus or minus sign between the terms.
- A polynomial problem involving two polynomials would look like: (ax^2 + bx + c) * (dy^2 + ey + f)
- Example: (2x^2 + 3x + 4)(5y^2 + 6y + 7)
- Note that the same methods for multiplying two three-term polynomials must also be applied to polynomials with four or more terms.
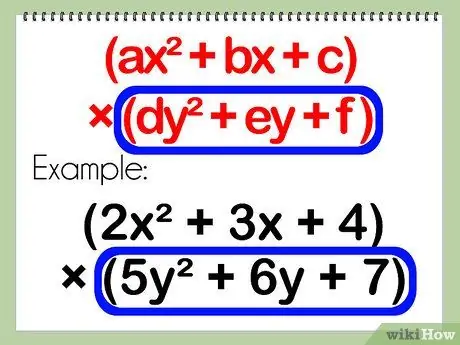
Step 2. Think of the second polynomial as a single term
The second polynomial must remain in one unit.
- The second polynomial refers to the part (dy^2 + ey + f) from the equation.
- Example: (5y^2 + 6y + 7)

Step 3. Distribute each part of the first polynomial to the second polynomial
Each part of the first polynomial must be translated and distributed to the second polynomial as a unit.
- In this step, the equation will look like: (ax^2)(dy^2 + ey + f) + (bx)(dy^2 + ey + f) + (c)(dy^2 + ey + f)
- Example: (2x^2)(5y^2 + 6y + 7) + (3x)(5y^2 + 6y + 7) + (4)(5y^2 + 6y + 7)

Step 4. Distribute each term
Distribute each of the new single-term polynomials over all the remaining terms in the three-term polynomial.
- Basically, in this step, the equation will look like: (ax^2)(dy^2) + (ax^2)(ey) + (ax^2)(f) + (bx)(dy^2) + (bx)(ey) + (bx)(f) + (c)(dy^2) + (c)(ey) + (c)(f)
- Example: (2x^2)(5y^2) + (2x^2)(6y) + (2x^2)(7) + (3x)(5y^2) + (3x)(6y) + (3x) (7) + (4)(5y^2) + (4)(6y) + (4)(7)

Step 5. Multiply the constants
Constants refer to the number digits in the problem. These constants are multiplied as usual according to the standard multiplication table.
- In other words, in this part of the problem, you are multiplying the parts a, b, c, d, e and f.
- Example: 10(x^2)(y^2) + 12(x^2)(y) + 14(x^2) + 15(x)(y^2) + 18(x)(y) + 21 (x) + 20(y^2) + 24(y) + 28

Step 6. Multiply the variables
Variables refer to the letters in the equation. When you multiply these variables, the different variables just need to be combined. However, when you multiply a variable by a similar variable, you increase the power of that variable by one.
- In other words, you're multiplying the x and y parts of the equation.
- Example: 10x^2y^2 + 12x^2y + 14x^2 + 15xy^2 + 18xy + 21x + 20y^2 + 24y + 28
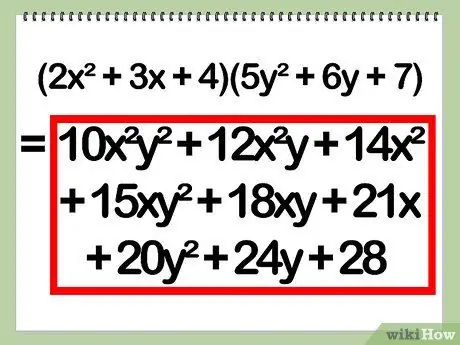
Step 7. Combine like terms and write down your final answer
This type of question is quite complicated so that it can produce like terms, namely two or more final terms that have the same final variable. If this is the case, you must add or subtract like terms as needed to determine your final answer. Otherwise, additional addition or subtraction is not required.






