- Author Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- Last modified 2025-06-01 06:05.
In a “system of equations”, you are asked to solve two or more equations simultaneously. When the two equations have two different variables, for example x and y, the solution may seem difficult at first. Luckily, once you know what you need to do, you can simply use your algebraic skills (and the science of calculating fractions) to solve the problem. Also learn how to draw these two equations if you are a visual learner, or are required by the teacher. Drawings will help you identify the subject matter or check the results of your work. However, this method is slower than the other methods, and cannot be used for all systems of equations.
Step
Method 1 of 3: Using the Substitution Method
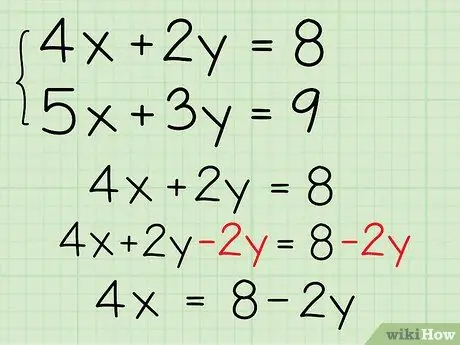
Step 1. Move the variables to the opposite side of the equation
The substitution method starts by “finding the value of x” (or any other variable) in one of the equations. For example, say the equation of the problem is 4x + 2y = 8 and 5x + 3y = 9. Start by working on the first equation. Rearrange the equation by subtracting 2y on both sides. Thus, you get 4x = 8 - 2y.
This method often uses fractions at the end. If you don't like counting fractions, try the elimination method below

Step 2. Divide both sides of the equation to "find the value of x"
Once the term x (or whatever variable you're using) is alone on one side of the equation, divide both sides of the equation by the coefficients so that only the variable remains. As an example:
- 4x = 8 - 2y
- (4x)/4 = (8/4) - (2y/4)
- x = 2 - y
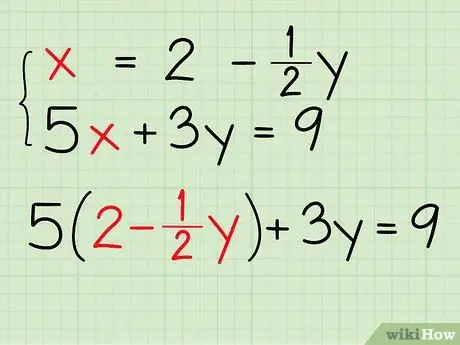
Step 3. Plug the x value from the first equation into the second equation
Make sure you plug it into the second equation, instead of the one you just worked on. Substitute (replace) the variable x in the second equation. Thus, the second equation now has only one variable. As an example:
- Is known x = 2 - y.
- Your second equation is 5x + 3y = 9.
- After swapping the x variable in the second equation with the x value from the first equation, we get "2 - y": 5(2 - y) + 3y = 9.

Step 4. Solve the remaining variables
Now, your equation has only one variable. Calculate the equation with ordinary algebraic operations to find the value of the variable. If the two variables cancel each other out, skip straight to the last step. Otherwise you'll get a value for one of the variables:
- 5(2 - y) + 3y = 9
- 10 - (5/2)y + 3y = 9
- 10 - (5/2)y + (6/2)y = 9 (If you don't understand this step, learn how to add fractions.)
- 10 + y = 9
- y = -1
- y = -2
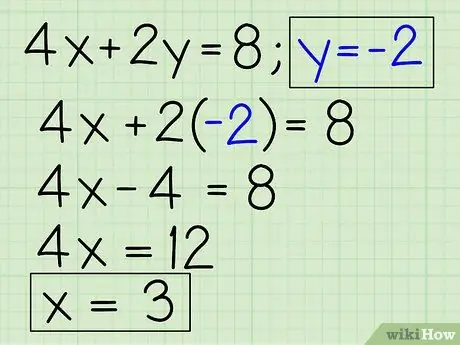
Step 5. Use the obtained answer to find the true value of x in the first equation
Don't stop just yet because your calculations aren't done yet. You must plug the obtained answer into the first equation to find the value of the remaining variables:
- Is known y = -2
- One of the equations in the first equation is 4x + 2y = 8. (You can use either one.)
- Replace the y variable with -2: 4x + 2(-2) = 8.
- 4x - 4 = 8
- 4x = 12
- x = 3

Step 6. Know what to do if the two variables cancel each other out
When you enter x=3y+2 or a similar answer to the second equation, meaning you're trying to get an equation that has only one variable. Sometimes, you just get the equation without variable. Double-check your work, and make sure you've put (reordered) equation one into equation two, instead of going back to the first equation. When you're sure you haven't done anything wrong, write one of the following results:
- If the equation has no variables and is not true (for example, 3 = 5), this problem have no answer. (When this is graphed, these two equations are parallel and never meet.)
- If the equation has no variables and Correct, (eg 3 = 3), meaning that the question has unlimited answers. Equation one is exactly the same as equation two. (When graphed, these two equations are the same line.)
Method 2 of 3: Using the Elimination Method
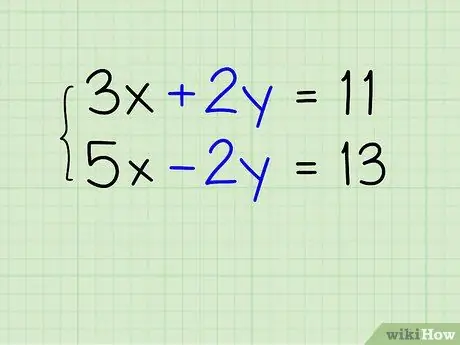
Step 1. Find the mutually exclusive variables
Sometimes, the equation in the problem is already cancel each other when added up. For example, if you do the equation 3x + 2y = 11 and 5x - 2y = 13, the terms "+2y" and "-2y" will cancel each other out and remove the variable "y" from the equation. Look at the equation in the problem, and see if there are variables that cancel each other out, as in the example. If not, continue to the next step.

Step 2. Multiply the equation by one so that one variable is removed
(Skip this step if the variables already cancel each other out.) If the equations don't have variables that cancel each other out by themselves, change one of the equations so they can cancel out each other. Take a look at the following examples so you can understand them easily:
- The equations in the problem are 3x - y = 3 and -x + 2y = 4.
- Let's change the first equation so that the variable y cancel each other out. (You may use the variable x. The final answer obtained will be the same.)
- Variable - y in the first equation must be eliminated by + 2y in the second equation. How, multiply - y with 2.
- Multiply both sides of the equation by 2, as follows: 2(3x - y)=2(3), so 6x - 2y = 6. Now, tribe - 2y will cancel each other out with +2y in the second equation.
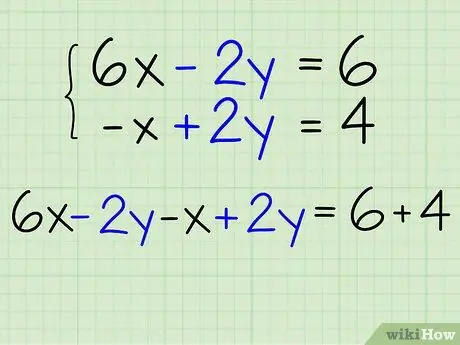
Step 3. Combine the two equations
To do this, add up the right side of the first equation with the right side of the second equation, and add up the left side of the first equation with the left side of the second equation. If done correctly, one of the variables will cancel each other out. Let's try to continue the calculation from the previous example:
- Your two equations are 6x - 2y = 6 and -x + 2y = 4.
- Add up the left sides of the two equations: 6x - 2y - x + 2y = ?
- Add up the right sides of the two equations: 6x - 2y - x + 2y = 6 + 4.
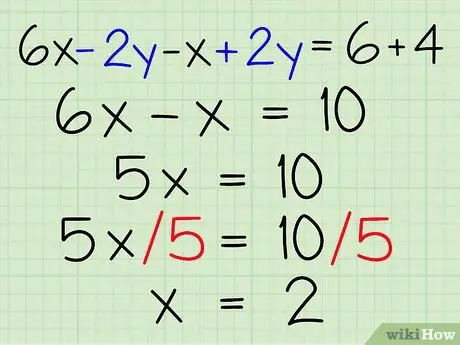
Step 4. Get the last variable value
Simplify your compound equation, and work with standard algebra to get the value of the last variable. If, after simplifying, the equation has no variables, continue to the last step in this section.
Otherwise, you will get a value for one of the variables. As an example:
- Is known 6x - 2y - x + 2y = 6 + 4.
- Group variables x and y together: 6x - x - 2y + 2y = 6 + 4.
- Simplify the equation: 5x = 10
- Find the x value: (5x)/5 = 10/5, to obtain x = 2.
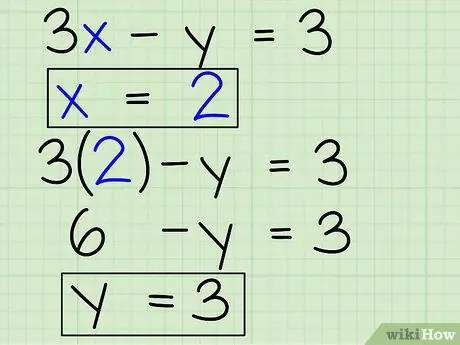
Step 5. Find the value of another variable
You've found the value of one variable, but what about the other? Plug your answer into one of the equations to find the value of the remaining variable. As an example:
- Is known x = 2, and one of the equations in the problem is 3x - y = 3.
- Replace the x variable with 2: 3(2) - y = 3.
- Find the value of y in the equation: 6 - y = 3
- 6 - y + y = 3 + y, so 6 = 3 + y
- 3 = y
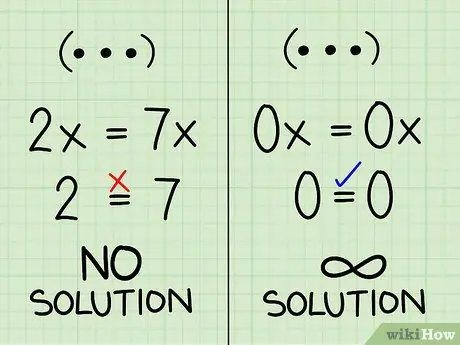
Step 6. Know what to do when the two variables cancel each other out
Sometimes, combining two equations results in an equation that doesn't make sense, or doesn't help you solve the problem. Review your work, and if you are sure that you did nothing wrong, write one of the following two answers:
- If the combined equation has no variables and is not true (for example, 2 = 7), this problem have no answer. This answer applies to both equations. (When this is graphed, these two equations are parallel and never meet.)
- If the combined equation has no variables and Correct, (eg 0 = 0), meaning that the question has unlimited answers. These two equations are identical to each other. (When graphed, these two equations are the same line.)
Method 3 of 3: Draw a Graph of Equations
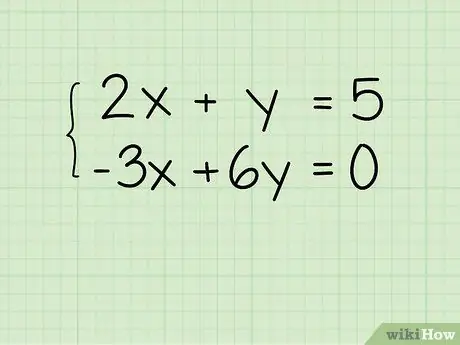
Step 1. Perform this method only when instructed
Unless you're using a computer or a graphing calculator, this method can only provide approximate answers. Your teacher or textbook may tell you to use this method to get into the habit of drawing equations as lines. This method can also be used to check the answer to one of the methods above.
The main idea is that you need to describe the two equations and find their point of intersection. The value of x and y at this point of intersection is the answer to the problem

Step 2. Find the y-values of both equations
Don't combine the two equations, and change each equation so that the format is "y = _x + _". As an example:
- Your first equation is 2x + y = 5. Change to y = -2x + 5.
- Your first equation is -3x + 6y = 0. Change to 6y = 3x + 0, and simplify to y = x + 0.
- If your two equations are exactly the same, the entire line is the "intersection" of the two equations. Write unlimited answers as an answer.
Step 3. Draw the coordinate axes
Draw a vertical “y-axis” line and a horizontal “x-axis” line on the graph paper. Starting at the point where the two axes intersect (0, 0), write down the number labels 1, 2, 3, 4, and so on sequentially pointing up on the y-axis, and pointing to the right on the x-axis. After that, write down the number labels -1, -2, and so on sequentially pointing down on the y-axis, and pointing to the left on the x-axis.
- If you don't have graph paper, use a ruler to make sure the spacing between each number is exactly the same.
- If you are using large numbers or decimals, we recommend that you scale your graph (e.g. 10, 20, 30 or 0, 1, 0, 2, 0, 3 instead of 1, 2, 3).
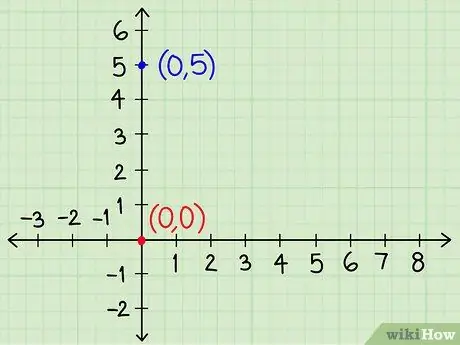
Step 4. Draw the y-intercept point for each equation
If the equation is in the form y = _x + _, you can start drawing a graph by making the point where the equation line intersects with the y-axis. The value of y is always the same as the last number in the equation.
-
Continuing the previous example, the first line (y = -2x + 5) intersects the y-axis at
Step 5.. second line (y = x + 0) intersects the y-axis at 0. (These points are written as (0, 5) and (0, 0) on the graph.)
- If possible, draw the first and second lines with different colored pens or pencils.
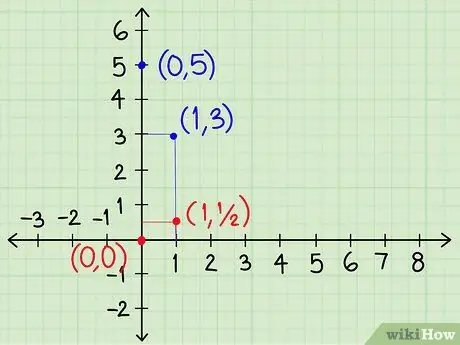
Step 5. Use the slope to continue the line
In equation format y = _x + _, the number in front of the x indicates the line's "slope level". Each time x is increased by one, the value of y will increase by the number of levels of slope. Use this information to find the points for each line on the graph when x = 1. (You can also enter x = 1 in each equation and find the value of y.)
- Continuing the previous example, the line y = -2x + 5 has a slope of -2. At point x = 1, the line moves down by 2 from the point x = 0. Draw a line connecting (0, 5) with (1, 3).
- Line y = x + 0 has a slope of ½. At x = 1, the line moves ride from the point x=0. Draw a line connecting (0, 0) with (1,).
- If two lines have the same slope, the two will never intersect. Thus, this system of equations has no answer. Write no answer as an answer.
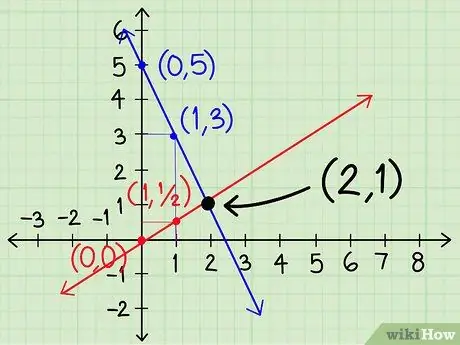
Step 6. Continue connecting the lines until the two lines intersect
Stop work and take a look at your graph. if the two lines have crossed each other, continue to the next step. If not, make a decision based on the position of your two lines:
- If the two lines approach each other, continue to connect the dots of your stripes.
- If the two lines move away from each other, go back and connect the dots in opposite directions, starting at x = 1.
- If the two lines are very far apart, try jumping over and connecting the points farther away, for example x = 10.
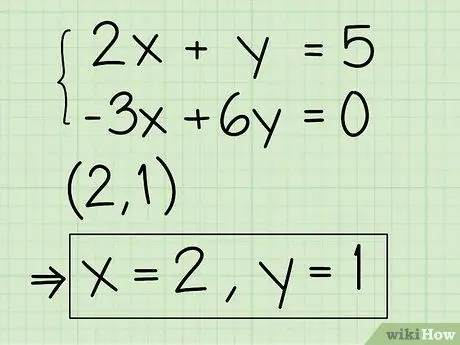
Step 7. Find the answer at the point of intersection
After the two lines intersect, the value of x and y at that point is the answer to your problem. If you are lucky, the answer will be a whole number. For example, in our example the two lines intersect at the point (2, 1) so the answer is x = 2 and y = 1. In some systems of equations, the point where the line intersects is between two whole numbers, and if the graph isn't very accurate, it's difficult to pinpoint where the x and y values are at the point of intersection. If allowed, you can write “x is between 1 and 2” as the answer, or use the substitution or elimination method to find the answer.
Tips
- You can check your work by plugging the answers into the original equation. If the equation turns out to be true (eg 3 = 3), it means that your answer is correct.
- When using the elimination method, sometimes you have to multiply the equation by a negative number so that the variables can cancel each other out.






