3 Ways to Solve Cubic Equations

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-16 19:04

When you first encounter the cubic equation (which is of the form ax ³ + bx ² + cx + d = 0), maybe you think that the problem will be difficult to solve. But know that solving cubic equations has actually been around for centuries! This solution, discovered by Italian mathematicians Niccolò Tartaglia and Gerolamo Cardano in the 1500s, is one of the first formulas known in ancient Greece and Rome. Solving cubic equations may be a little difficult, but with the right approach (and sufficient knowledge), even the most difficult cubic equations can be solved.

Step

Method 1 of 3: Solving Using Quadratic Equations

Step 1. Check if your cubic equation has a constant

As stated above, the form of the cubic equation is ax ³ + bx ² + cx + d = 0. b, c, and the value of d can be 0 without affecting the form of this cubic equation; this basically means that the cubic equation doesn't always have to include the value of bx ², cx, or d to be a cubic equation. To start using this fairly easy way of solving cubic equations, check to see if your cubic equation has a constant (or a value of d). If your equation doesn't have a constant or value for d, then you can use a quadratic equation to find the answer to the cubic equation after a few steps.

On the other hand, if your equation has a constant value, then you will need another solution. See the steps below for other approaches

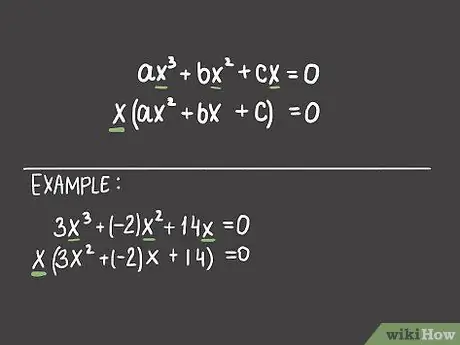
Step 2. Factor the x value from the cubic equation

Since your equation has no constant value, all components in it have the variable x. This means that this value of x can be factored out of the equation to simplify it. Do this step and rewrite your cubic equation in the form x (ax ² + bx + c).

For example, let's say that the original cubic equation here is 3 x ³ + -2 x ² + 14 x = 0. By factoring one variable x from this equation, we get the equation x (3 x ² + -2 x + 14) = 0.

Step 3. Use quadratic equations to solve the equations in brackets

You may notice that some of your new equations, which are enclosed in parentheses, are in the form of a quadratic equation (ax ² + bx + c). This means that we can find the value needed to make this equation equal to zero by plugging a, b, and c into the quadratic equation formula ({- b +/-√ (b ²- 4 ac)}/2 a). Perform these calculations to find two answers to your cubic equation.

• In our example, plug the values of a, b, and c (3, -2, and 14, respectively) into the quadratic equation as follows:

  {- b +/-√ (b ²- 4 ac)}/2 a

  {-(-2) +/-√ ((-2)²- 4(3)(14))}/2(3)

  {2 +/-√ (4 - (12)(14))}/6

  {2 +/-√ (4 - (168)}/6

  {2 +/-√ (-164)}/6

• Answer 1:

  {2 + √(-164)}/6

  {2 + 12.8 i }/6

• Answer 2:

  {2 - 12.8 i }/6

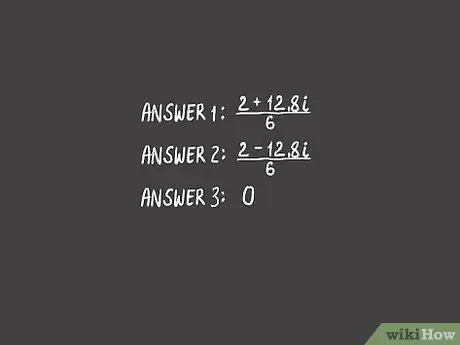
Step 4. Use zeros and your answer to your quadratic equation as your answer to your cubic equation

Quadratic equations will have two answers, whereas cubic equations have three answers. You already know two answers out of three; which you get from the "squared" part of the equation in brackets. If your cubic equation can be solved by "factorization" like this, your third answer is almost always 0. Safe! You have just solved a cubic equation.

The reason that makes this method work is the fundamental fact that "any number multiplied by zero equals zero". When you factor your equation into the form x (ax ² + bx + c) = 0, you basically just divide it into two "parts"; one part is the x variable on the left side and the other part is the quadratic equation in brackets. If one of these two parts is zero, then the whole equation will also be zero. Thus, the two answers to the quadratic equation in parentheses, which would make it zero, are the answers to the cubic equation, as well as 0 itself - which would make the part on the left-hand side also zero.

Method 2 of 3: Finding Integer Answers Using a Factor List

Step 1. Make sure that your cubic equation has a constant value

While the methods described above are fairly easy to use because you don't have to learn a new calculation technique to use them, they won't always help you solve cubic equations. If your cubic equation is of the form ax ³ + bx ² + cx + d = 0, where the value of d is not equal to zero, the "factorization" method above doesn't work, so you'll need to use one of the methods in this section to solve this.

For example, let's say we have the equation 2 x ³ + 9 x ² + 13 x = -6. In this case, to get zero on the right side of the equation, we must add 6 to both sides. After that, we will get a new equation 2 x ³ + 9 x ² + 13 x + 6 = 0, with a value of d = 6, so we cannot use the "factorization" method as in the previous method.

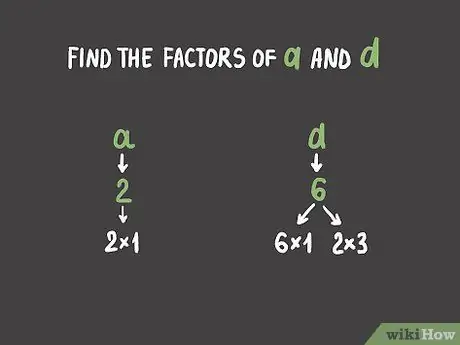
Step 2. Find the factors of a and d

To solve your cubic equation, start by finding the factor of a (the coefficient of x ³) and d (the constant value at the end of the equation). Remember, factors are numbers that can be multiplied by each other to produce a certain number. For example, since you can get 6 by multiplying 6 × 1 and 2 × 3, 1, 2, 3, and 6 are factors of 6.

• In the example problem we are using, a = 2 and d = 6. The factor of 2 is 1 and 2. While the factor of 6 is 1, 2, 3, and 6.

  

  Step 3. Divide the factor a by the factor of d

  Next, list the values you get by dividing each factor of a by each factor of d. This calculation usually results in many fractional values and several whole numbers. The integer value to solve your cubic equation is one of the integers obtained from the calculation.

  In our equation, divide the factor value of a (1, 2) by the factor of d (1, 2, 3, 6) and get the following results: 1, 1/2, 1/3, 1/6, 2, and 2/3. Next, add negative values to the list, and we get: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3, and -2/3. The answer to the cubic equation -- which is an integer, is on the list.

  

  Step 4. Use synthetic division to check your answers manually

  Once you've got a list of values like the one above, you can look up the integer values that are the answers to your cubic equation by manually entering each integer, and find out which value is equal to zero. However, if you don't want to spend time doing this, there's a way to do it more quickly, namely with a calculation called synthetic division. Basically, you would divide your integer value by the original coefficients of a, b, c, and d in your cubic equation. If the remainder is zero, then that value is one of the answers to your cubic equation.

  • Synthetic division is a complex topic - see the link below for more information. Here's an example of how to find one of the answers to your cubic equation with synthetic division:

    -1 | 2 9 13 6

    _| -2-7-6

    _| 2 7 6 0

    Since we get the final result equal to 0, we know that one of the integer answers to our cubic equation is -1.

  Method 3 of 3: Using the Discriminant Approach

  

  Step 1. Write down the equations a, b, c, and d

  To find the answer to the cubic equation in this way, we will do a lot of calculations with the coefficients in our equation. Because of this, it's a good idea to note down the values of a, b, c, and d before you forget any of the values.

  For example, for the equation x ³ - 3 x ² + 3 x - 1, write it down as a = 1, b = -3, c = 3, and d = -1. Don't forget that when the variable x has no coefficient, its value is 1.

  

  Step 2. Calculate 0 = b ² - 3 air conditioners.

  The discriminant approach to finding answers to cubic equations requires complex calculations, but if you follow the steps carefully, it can be very useful for solving cubic equations that are difficult to solve in other ways. To begin with, find the value of 0, which is the first significant value of the several we need, plugging the appropriate value into the formula b ² - 3 air conditioners.

  • In the example we're using, we'll solve it as follows:

    b ² - 3 ac

    (-3)² - 3(1)(3)

    9 - 3(1)(3)

    9 - 9 = 0 = 0

  

  Step 3. Calculate 1= 2 b ³ - 9 abc + 27 a ² d.

  The next significant value we need, 1, requires a longer calculation, but can be found in the same way as 0. Plug the appropriate value into the formula 2 b ³ - 9 abc + 27 a ² d to get the value of 1.

  • In this example, we solve it as follows:

    2(-3)³ - 9(1)(-3)(3) + 27(1)²(-1)

    2(-27) - 9(-9) + 27(-1)

    -54 + 81 - 27

    81 - 81 = 0 = 1

  

  Step 4. Calculate = 1² - 4Δ0³) -27 a ².

  Next, we calculate the "discriminant" value of the values 0 and 1. The discriminant is a number that gives you information about the root of the polynomial (you may have unconsciously memorized the quadratic discriminant formula: b ² - 4 air conditioners). In the case of a cubic equation, if the value of the discriminant is positive, then the equation has three real number answers. If the discriminant value is equal to zero, then the equation has one or two real number answers, and some of the answers have the same value. If the value is negative, then the equation has only one real number answer, because the graph of the equation will always intersect the x-axis at least once.)

  • In this example, since both 0 and 1 = 0, finding the value of is very easy. We just need to calculate it in the following way:

    1² - 4Δ0³) -27 a ²

    (0)² - 4(0)³) ÷ -27(1)²

    0 - 0 ÷ 27

    0 =, so our equation has 1 or 2 answers.

  

  Step 5. Calculate C = ³(√((Δ1² - 4Δ0³) + 1)/ 2).

  The last value that is important for us to get is the value of C. This value allows us to get all three roots of our cubic equation. Solve as usual, plugging the values of 1 and 0 into the formula.

  • In this example, we will get the value of C by:

    ³(√((Δ1² - 4Δ0³) + 1)/ 2)

    ³√(√((0² - 4(0)³) + (0))/ 2)

    ³√(√((0 - 0) + (0))/ 2)

    0 = C

  

  Step 6. Calculate the three roots of the equation with your variable

  The root (answer) of your cubic equation is determined by the formula (b + u C + (Δ0/u C)) / 3 a, where u = (-1 + (-3))/2 and n is equal to 1, 2, or 3. Plug your values into the formula to solve them - there may be quite a few calculations you need to do, but you should get all three of your cubic equation answers!

  • In this example, we might solve it by checking the answers when n equals 1, 2, and 3. The answer we get from this calculation is the possible answer to our cubic equation - any value we plug into the cubic equation and it gives the same result. with 0, is the correct answer. For example, if we get an answer equal to 1 if in one of our calculation experiments, plugging the value 1 into the equation x ³ - 3 x ² + 3 x - 1 yields the final result equal to 0. Thus

    Step 1. is one of the answers to our cubic equation.