Integral in calculus is the opposite of differentiation. Integral is the process of calculating the area under a curve bounded by xy. There are several integral rules, depending on the type of polynomial present.
Step
Method 1 of 2: Simple Integral
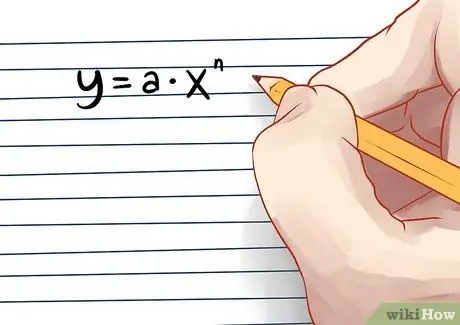
Step 1. This simple rule for integrals works for most basic polynomials
Polynomial y = a*x^n.
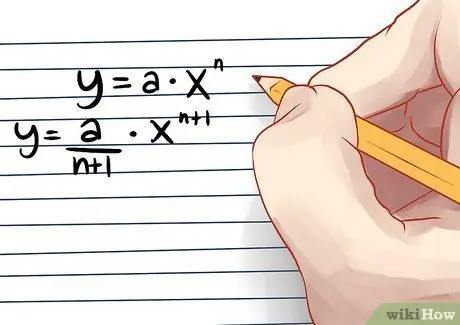
Step 2. Divide (coefficient) a by n+1 (power+1) and increase the power by 1
In other words, the integral y = a*x^n is y = (a/n+1)*x^(n+1).
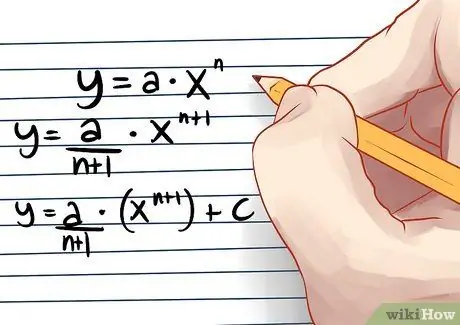
Step 3. Add the integral constant C for the indeterminate integral to correct for inherent ambiguity about the exact value
Therefore, the final answer to this question is y = (a/n+1)*x^(n+1) + C.
Think of it this way: when deriving a function, every constant is omitted from the final answer. Therefore, it is always possible that the integral of a function has some arbitrary constant
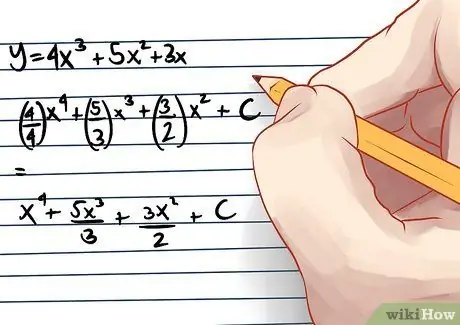
Step 4. Integrate the separate terms in a function separately with the rule
For example, the integral of y = 4x^3 + 5x^2 +3x is (4/4)x^4 + (5/3)*x^3 + (3/2)*x^2 + C = x^4 + (5/3)*x^3 + (3/2)*x^2 + C.
Method 2 of 2: Other Rules
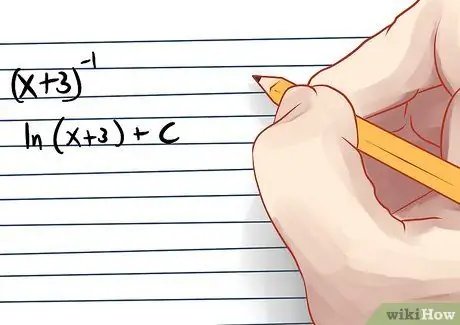
Step 1. The same rules don't apply to x^-1, or 1/x
When you integrate a variable to the power of 1, the integral is natural log of variable. In other words, the integral of (x+3)^-1 is ln(x+3) + C.
Step 2. The integral of e^x is the number itself
The integral of e^(nx) is 1/n * e^(nx) + C; thus, the integral of e^(4x) is 1/4 * e^(4x) + C.
Step 3. The integrals of the trigonometric functions must be memorized
You must remember all of the following integrals:
-
The integral of cos(x) is sin(x) + C.
Integrate Step 7Bullet1 -
The integral sin(x) is -cos(x) + C. (note the negative sign!)
Integrate Step 7Bullet2 -
With these two rules, you can derive the integral of tan(x), which is equivalent to sin(x)/cos(x). The answer is -ln|cos x| + C. Check the results again!
Integrate Step 7Bullet3
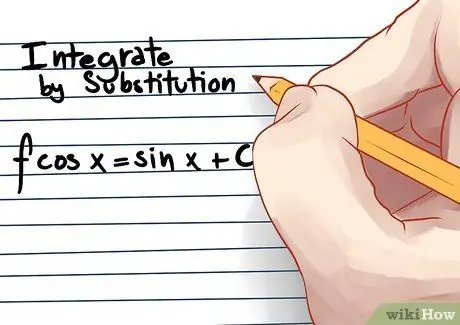
Step 4. For more complex polynomials like (3x-5)^4, learn how to integrate with substitution
This technique introduces a variable such as u, as a multiterm variable, for example 3x-5, to simplify the process while applying the same basic integral rules.
