6 Ways to Find the Domain of a Function

2024 Author: Jason Gerald | [email protected]. Last modified: 2024-01-15 08:07

The domain of a function is the set of numbers that can be entered into a function. In other words, a domain is a set of x values that can be plugged into any given equation. The set of possible y values is called a range. If you want to know how to find the domain of a function in various situations, follow these steps.

Step

Method 1 of 6: Learning the Basics

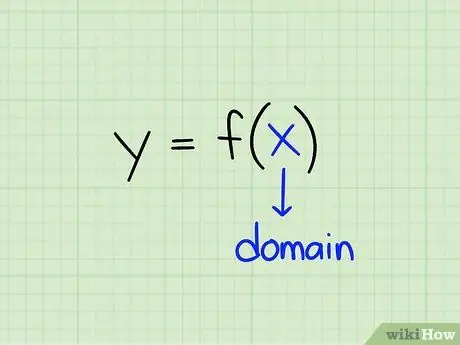
Step 1. Learn the definition of a domain

Domain is defined as a set of input values that a function uses to produce output values. In other words, a domain is a complete set of x values that can be entered into a function to return a y value.

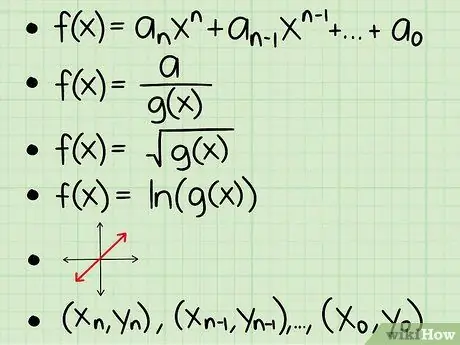
Step 2. Learn how to find the domain of various functions

The type of function will determine the best way to search for the domain. Here are the basics you need to know about each type of function, which will be explained in the next section:

• A polynomial function without roots or variables in the denominator.

  For this type of function, the domain is all real numbers.

• Fractional function with a variable in the denominator.

  To find the domain of this function, make the bottom equal to zero and take the value of x out when solving the equation.

• A function with a variable in the root sign.

  To find the domain of this type of function, create a variable in the square root >0 and work it out to find the possible x values.

• Functions that use the natural logarithm (ln).

  Make a part in brackets > 0 and finish.

• Chart.

  Look at the graph for possible x values.

• Connection.

  This is a list of x and y coordinates. Your domain is just a list of x coordinates.

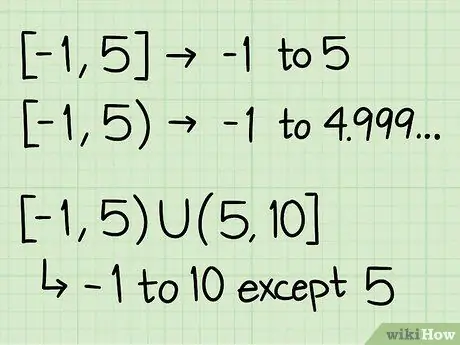
Step 3. Define the domain correctly

The correct notation for the domain is easy to learn, but it is important that you write it correctly to represent the correct answer and get a perfect score in assignments and exams. Here are some things you need to know about writing domain functions:

• The form of domain writing is open parenthesis, followed by two domain dot boundaries separated by a comma, followed by a closed parenthesis.

  For example, [-1, 5). This means that the domains are from -1 to 5

• Use brackets like [and] to indicate numbers that belong to the domain.

  So in this example, the domain includes -1

• Use brackets like (and) to indicate numbers that don't belong to the domain.

  So in the example, [-1, 5), 5 is not included in the domain. The domain stops just before 5, for example 4,999…

• Use “U” (meaning “union”) to join parts of a domain separated by distance.'

  • For example, [-1, 5) U (5, 10]. That is, the domain is from -1 to 10, the numbers -1 and 10 are included, but there is a distance in the domain 5. This may be the result, for example, of a function with the denominator x -5.
  • You can use as many U symbols as needed if the domain has a lot of spacing.

• Use the infinity sign and the infinite negative to indicate the infinite domain in any direction.

  Always use (), not , with an infinity sign

Method 2 of 6: Finding the Domain of a Fractional Function

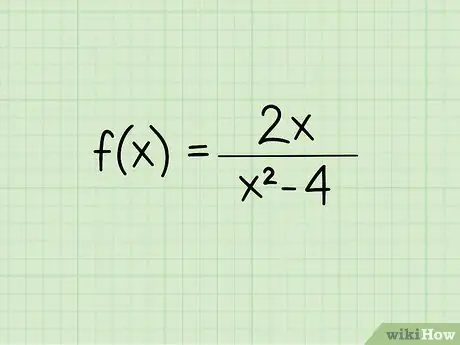
Step 1. Write down the problem

Suppose you want to solve the following problem:

f(x) = 2x/(x² - 4)

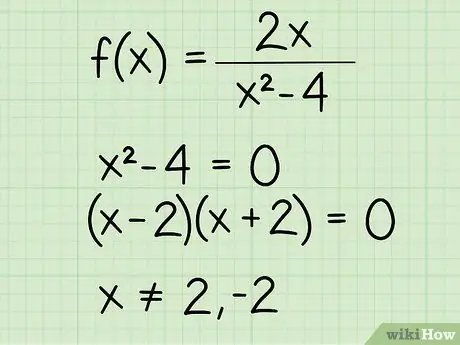
Step 2. For fractions with a variable in the denominator, make the denominator equal to zero

When looking for the domain of a fractional function, you have to take out all the values of x to make the denominator equal to zero because you can't divide anything by zero. So, write the denominator as an equation and make it equal to 0. Here's how to do it:

• f(x) = 2x/(x² - 4)
• x² - 4 = 0
• (x - 2)(x + 2) = 0
• x (2, - 2)

Step 3. Write down the domain

Here's how::

x = all real numbers except 2 and -2

Method 3 of 6: Finding the Domain of a Function with a Square Root

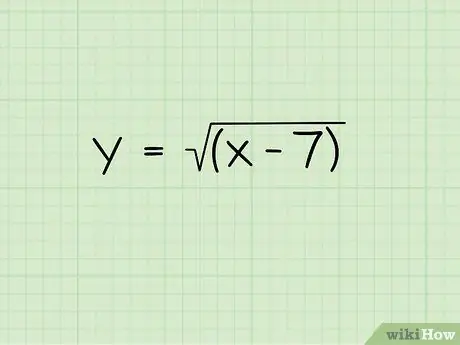
Step 1. Write down the problem

Suppose you want to solve the following problem: Y =√(x-7)

Step 2. Make the part inside the root greater than or equal to 0

You can't take the square root of a negative number, although you can take the square root of 0. So, make the part inside the root greater than or equal to 0. Note that this applies not only to the square root, but to all square roots. even number. However, it doesn't apply to the square root of odd numbers because negative numbers under odd roots don't matter. Here's how:

x-7 0

Step 3. Remove the variables

To remove x from the left side of the equation, add 7 to both sides, leaving:

x 7

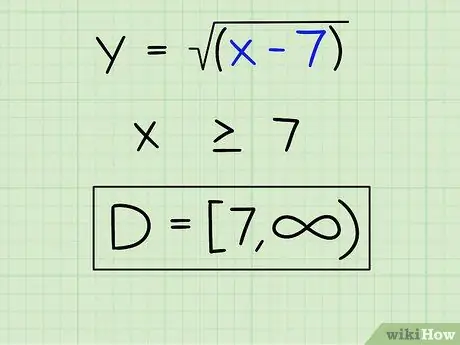
Step 4. Write down the domain correctly

Here's how to write it:

D = [7,)

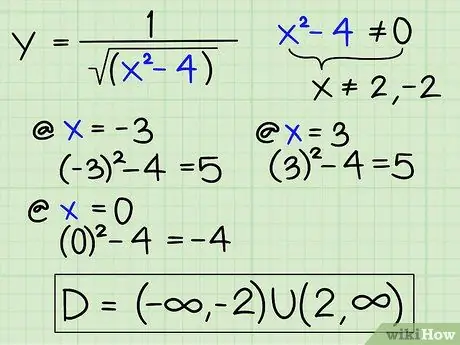
Step 5. Find the domain of the function with the square root if there are multiple solutions

Suppose you want to solve the following function: Y = 1/√(x² -4). When you factor the denominator and make it zero, you get x (2, - 2). Here's what you should do next:

• Now, examine the domain under -2 (by entering the value -3, for example), to see if a number below -2 can be inserted into the denominator to find a number above 0.

  (-3)² - 4 = 5

• Now, check the domain between -2 and 2. Choose 0, for example.

  0² - 4 = -4, so you know a number between -2 and 2 is impossible.

• Now try numbers above 2, for example +3.

  3² - 4 = 5, so numbers above 2 are possible.

• Write down the domain when you're done. Here's how to write the domain:

  D = (-∞, -2) U(2,)

Method 4 of 6: Finding the Domain of a Function with Natural Log

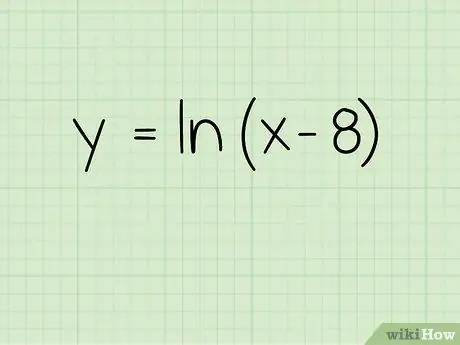
Step 1. Write down the problem

Suppose you want to complete the following:

f(x) = ln(x-8)

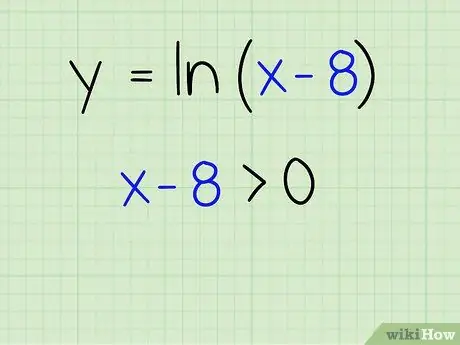
Step 2. Make the part in the brackets greater than zero

Natural log (ln) must be a positive number, so make the part in parentheses greater than zero. Here's what you should do:

x - 8 > 0

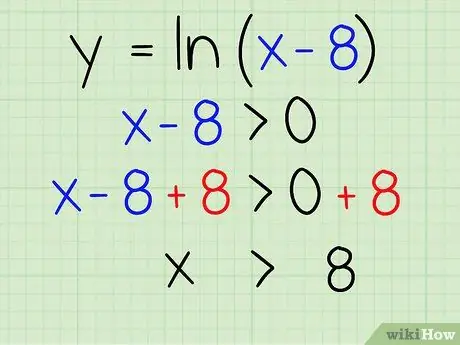
Step 3. Finish

Find the value of x by adding 8 to both sides. Here's how:

• x - 8 + 8 > 0 + 8
• x > 8

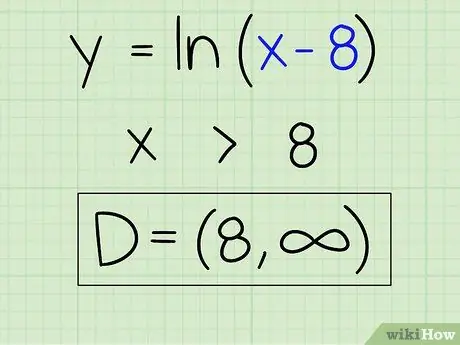
Step 4. Write down the domain

Show that the domain of this equation is all numbers greater than 8 to infinity. Here's how:

D = (8,)

Method 5 of 6: Finding the Domain of a Function from a Graph

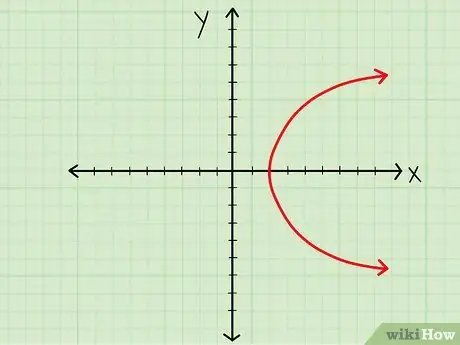
Step 1. Look at the chart

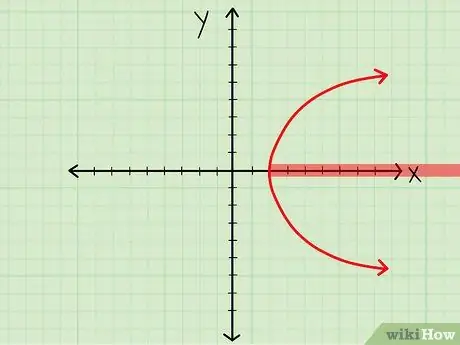
Step 2. Pay attention to the value of x in the graph

This may be easier said than done, but here are a few tips:

• Line. If you look at a line in an infinite graph, then all x is the domain, so the domain is all real numbers.
• Ordinary satellite dish. If you look at a parabola that opens up or down, then yes, the domain is all real numbers because all numbers in the x direction are the domain.
• Side dish. If you have a parabola with a vertex (4, 0) that extends indefinitely to the right, then your domain is D = [4,).

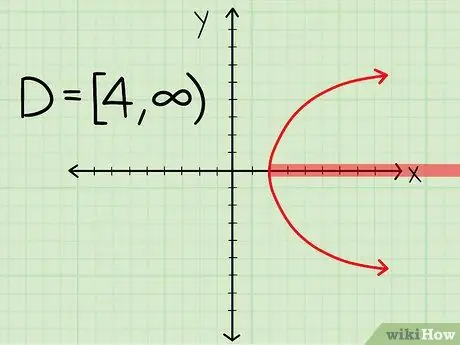
Step 3. Write down the domain

Write down the domain based on the type of graph you encounter. If you're not sure and know which equation to use, plug the x-coordinates into the function to check.

Method 6 of 6: Finding the Domain of a Function Using Relationships

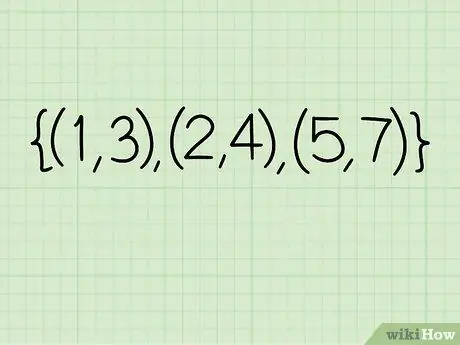
Step 1. Write down the relationship

A relationship is simply a collection of x and y coordinates. Say you want to solve the following coordinates: {(1, 3), (2, 4), (5, 7)}

Step 2. Write down the x-coordinates, namely:

1, 2, 5.

Step 3. Write down the domain

D = {1, 2, 5}

Step 4. Make sure the relationship is a function

The condition of a relationship is a function, that is, every time you enter a number of x coordinates, you will get the same y coordinates. So, if you enter x = 3, y = 6, and so on. The following relationship is not a function because you get two different y values for each x value: {(1, 4), (3, 5), (1, 5)}.