A basic part of learning algebra is learning how to find the inverse of a function, or f(x). The inverse of a function is represented by f^-1(x), and the inverse is usually represented visually as the initial function reflected by the line y=x. This article will show you how to find the inverse of a function.
Step
Step 1. Make sure your function is a one-to-one (injective) function
Only one-to-one functions have an inverse.
-
A function is a one-to-one function if it passes the vertical line test and the horizontal line test. Draw a vertical line through the entire graph of the function and count the number of times it hits the function. Then, draw a horizontal line through the entire graph of the function and count the number of occurrences of this line on the function. If each line only hits the function once, then the function is a one-to-one function.
If a graph does not pass the vertical line test, it is not a function
-
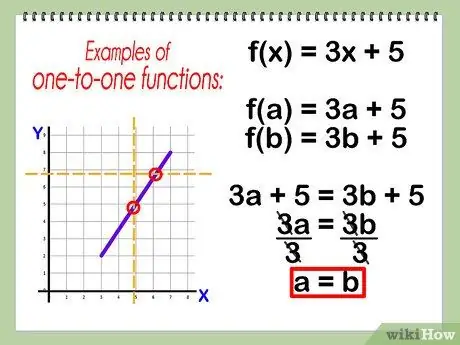
To determine algebraically if a function is a one-to-one function, plug f(a) and f(b) into your function to see if a = b. For example, take f(x) = 3x+5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Thus, f(x) is a one-to-one function.
Step 2. Since this is a function, change the x and y
Remember that f(x) is a substitute for "y."
- In a function, "f(x)" or "y" represents the output and "x" represents the input. To find the inverse of a function, you swap the input and output.
- Example: Let's use f(x) = (4x+3)/(2x+5) – which is a one-to-one function. By swapping x and y, we get x = (4y + 3)/(2y + 5).
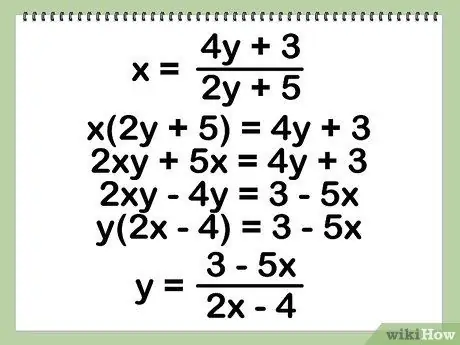
Step 3. Find the new "y"
You have to change the expression to find y, or to find new operations to be performed on the input to get the inverse as the output.
- This can be tricky, depending on your expression. You may need to use algebraic tricks like cross multiplication or factoring to evaluate expressions and simplify them.
-
In our example, we will perform the following steps to isolate y:
- We start with x = (4y + 3)/(2y + 5)
- x(2y + 5) = 4y + 3 – Multiply both sides by (2y + 5)
- 2xy + 5x = 4y + 3 – Distribute x
- 2xy - 4y = 3 - 5x – Move all the y terms to one side
- y(2x - 4) = 3 - 5x – Distribute in reverse to combine the terms y
- y = (3 - 5x)/(2x - 4) – Divide to get your answer
Step 4. Replace the new "y" with f^-1(x)
This is the equation for the inverse of your original function.
